Обобщенная схема импульсной системы.

ИЭ

=

=

_|_

Эта система замыкается только в момент квантования (сигнал проходит), а … момента – система разомкнута.

Импульсная система может быть представлена в виде совокупности непрерывных звеньев, описываемых ………… и ИЭов.

Преобразование Лапласа импульсного сигнала. Z-преобразование.

Решетчатая функция

Сигнал:

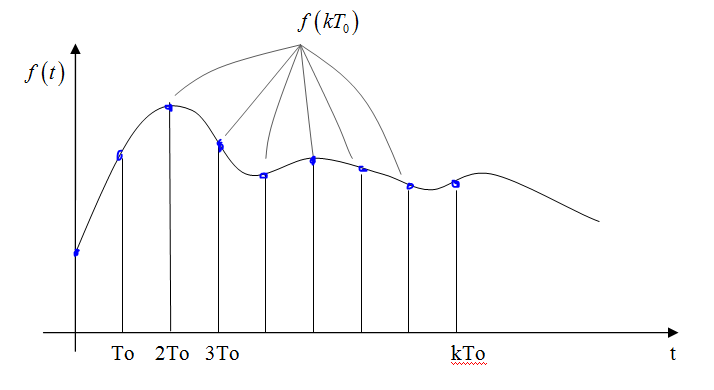
Решетчатая функция определяется набором значений непрерывного сигнала в тактовые моменты времени.

Если есть непрерывный сигнал – для его своя решетчатая функция

[ ] – значит это набор дискретных значений

Решетчатая функция – это функция, К целочисленного .

Рассмотрим элементарную импульсную цепь:

_|_

- это набор от 0 до импульсов.

Возьмем обычное преобразование Лапласа:

Преобразование от = сумме преобразований, и преобразование от это 1.

-й ряд

Это преобразование Лапласа импульсного сигнала.

Введем некоторое Z-преобразование. Оно будет связывать некоторый оригинал , если эта функция не существует, т.е. , при k<0.

, преобразовав М и , что выполняется равенство.

Тогда можно использовать некоторое соотношение:

Z-преобразование функции – это преобразование Лапласа импульсного сигнала с учетом подстановки

Основные свойства z-преобразования:

1. Линейность. Это следует из формулы; имеется ввиду …….. и суперпозиция.

2. Сдвиг аргумента

- целое число.

Это сдвиг в сторону опережения

… сдвиг в сторону запаздывания.

3. Начальное и конечное значение аргумента

Если этот предел существует.

Например, если система неустойчива, её процесс ни к чему не стремится.

4. Свертка двух решетчатых функций.

Есть

Т.е. если это произведение в изображениях, то это свертка …… сигналов.

5. Обратное z-преобразования и его вычисления.

1. Его можно вычислить методом разложения изображения в ряд Лорана.

2. Получение оригинала по известному изображению. Использование методов вычетов. Это аналитический метод.

1. 

По определению, если представить в виде ряда. То коэффициент при точно соответствует значению оригинала в момент . Что бы получить оригинал, нужно разложит изображение в ряд.

Если , то разложение в ряд осуществляется цикличным делением на .

Пример:

Вычисление оригинала, разложение в ряд.

1

K

Достоинство – простота.

Недостаток – нет аналитического выражения и этот метод приводит к накоплению ошибок.

2. Аналитический метод вычисления обратного z-преобразования (см. “Пространство состояния в теории систем”)

Пусть

Простой полюс

Кратный полюс; кратность :

Сначала берется , потом дифференцируем по Z, и только потом подставляем .

Для вычисления z-преобразования необходимо:

1. Вычислить полюсы и определить простые и кратные.

2. Вычислить вычеты в определенных полюсах

3. Просуммировать отдельные составляющие

Пример:

Задано

, тогда …., т.е.

если , то предела не будет.

Лекция_3