Операции с векторами и их свойства
Суммой
векторов ![]() и
и
![]() называется
вектор
называется
вектор
![]()
![]() Для любых векторов
Для любых векторов
![]() справедливы равенства
справедливы равенства
|
|
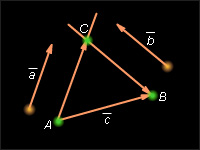
Теорема 11.6.
Каковы
бы ни были три точки A,
B и C,
имеет место векторное равенство
![]()
Доказательство
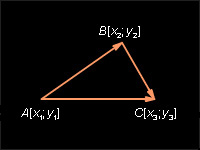
Пусть A (x1; y1), B (x2; y2), C (x3; y3) – данные точки. Вектор
имеет
координаты
Замечание.
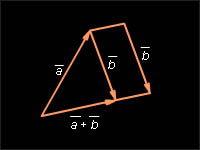
Теорема 11.6 дает следующий способ
построения суммы произвольных векторов
и
|
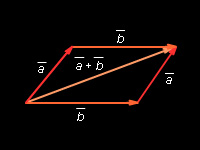
Правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
|
Рисунок 11.2.3. Правило параллелограмма |
Разностью
векторов
и
называется
такой вектор
![]() который
в сумме с вектором
дает
вектор
который
в сумме с вектором
дает
вектор
![]()
![]() откуда c1 = a1– b1;
c2 = a2– b2.
откуда c1 = a1– b1;
c2 = a2– b2.
Произведением
вектора
на
число λ называется
вектор
![]() т. е.
т. е.
![]()
Для любого вектора и чисел λ и μ
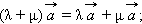
Для любых двух векторов и и числа λ
|
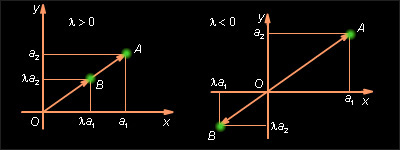
Теорема 11.7.
Абсолютная
величина вектора
![]() равна
|λ || a|.
Направление вектора
при
равна
|λ || a|.
Направление вектора
при
![]() совпадает
с направлением вектора
если
λ > 0, и противоположно направлению
вектора
если
λ < 0.
совпадает
с направлением вектора
если
λ > 0, и противоположно направлению
вектора
если
λ < 0.
Доказательство
Построим
векторы
Поэтому, если λ > 0, то точка B лежит на луче OA, а следовательно, векторы и одинаково направлены. Если λ < 0, то точка B лежит на дополнительном луче и векторы и противоположно направлены. Абсолютная
величина вектора
равна
|
Теорема 11.8.
Для
любых отличных от нуля коллинеарных
векторов
и
существует
такое число λ, что
![]()
Доказательство
Пусть
и
одинаково
направлены. Векторы
и
|
Теорема 11.9.
Пусть
и
–
отличные от нуля неколлинеарные векторы.
Любой вектор
![]() можно
единственным образом представить в
виде
можно
единственным образом представить в
виде
![]()
Доказательство
Пусть
A и B
– начало и конец вектора
Для
доказательства единственности
представления допустим, что в условиях
теоремы такое представление не
единственно. То есть наряду с числами
λ и μ такими, что
|
Скалярное произведение векторов.
Скалярным
произведением векторов
и
называется
число
![]() Скалярное
произведение векторов
и
обозначется
Скалярное
произведение векторов
и
обозначется
![]()
Для
любых векторов
и
![]() верно:
верно:
Теорема 11.10.
Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Доказательство
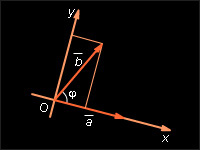
Пусть и – данные векторы и φ – угол между ними. Имеем:
или
Скалярное
произведение
|
Единичные
векторы
![]() и
и
![]() имеющие
направления положительных координатных
полуосей, называются координатными
векторами или ортами.
имеющие
направления положительных координатных
полуосей, называются координатными
векторами или ортами.
Теорема 11.11.
Любой
ненулевой вектор
единственным
образом можно разложить по координатным
векторам, то есть записать в виде
![]()
Доказательство
Так
как координатные векторы отличны от
нуля и неколлинеарны, то любой вектор
допускает
разложение по этим векторам в силу
теоремы 11.9
|
Базисом на плоскости называются два любых неколлинеарных вектора этой плоскости, взятые в определенном порядке.
Пусть
![]() и
и
![]() –
некоторый базис и
–
произвольный вектор, тогда по теореме
11.9 и следствию 11.1 существуют два
единственным образом определенных
числа x и y, такие, что
–
некоторый базис и
–
произвольный вектор, тогда по теореме
11.9 и следствию 11.1 существуют два
единственным образом определенных
числа x и y, такие, что
|
Числа
x и y называются координатами
вектора
в
данном базисе. В этом случае также пишут
![]()
Справедливы следующие свойства.
Теорема 11.12.
При умножении вектора на число все его координаты в данном базисе умножаются на это число.
При сложении двух или больше векторов их соответственные координаты складываются.
Доказательство
Пусть
|
Пусть
на плоскости заданы точка O и произвольный
базис
![]() Совокупность этого базиса и точки O
называется декартовой системой
координат
Совокупность этого базиса и точки O
называется декартовой системой
координат ![]() Точка O называется началом координат.
Если через эту точку O провести прямые
в направлениях, заданных базисными
векторами
и
Точка O называется началом координат.
Если через эту точку O провести прямые
в направлениях, заданных базисными
векторами
и
![]() то
полученные прямые называются осями
координат: прямая OX – осью абсцисс,
прямая Oy – осью ординат. Координаты
радиус-вектора точки M называются
координатами этой точки в данной системе
координат (x – абцисса, y – ордината).
то
полученные прямые называются осями
координат: прямая OX – осью абсцисс,
прямая Oy – осью ординат. Координаты
радиус-вектора точки M называются
координатами этой точки в данной системе
координат (x – абцисса, y – ордината).
|
Рисунок 11.3.1 |
Если
и
взаимно
перпендикулярны и их модули равны
единице, то базис называется
ортонормированным, и мы получим известную
нам прямоугольную декартову
систему координат на плоскости. Таким
образом, рассмотренная здесь декартова
система координат
![]() является
обобщением рассмотренной ранее
прямоугольной декартовой системы
координат, которая в свою очередь
является частным случаем общей декартовой
системы координат.
является
обобщением рассмотренной ранее
прямоугольной декартовой системы
координат, которая в свою очередь
является частным случаем общей декартовой
системы координат.
Мы
видели (теорема 11.12), что свойства сложения
и умножения вектора на число, записанные
через координаты вектора, в произвольном
базисе сохраняются. Рассмотрим, как
изменится выражение для скалярного
произведения, записанное через их
координаты в произвольном базисе. Итак,
пусть
–
произвольный базис,
![]() и
и
![]() –
любые два вектора. Рассмотрим скалярное
произведение этих векторов и преобразуем
его, используя ранее доказанные свойства:
–
любые два вектора. Рассмотрим скалярное
произведение этих векторов и преобразуем
его, используя ранее доказанные свойства:
|
Таким
образом, для вычисления скалярного
произведения двух векторов в произвольном
базисе, кроме их координат, надо знать
модули базисных векторов и угол между
ними. Очевидно, что если базис
ортонормирован, то
![]()
![]() и
мы получим известную формулу для
скалярного произведения в ортогональной
декартовой системе координат.
и
мы получим известную формулу для
скалярного произведения в ортогональной
декартовой системе координат.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства (см., например, доказательство теоремы 11.10). Часто одно и то же множество приходится рассматривать в разных координатах. Одна и та же точка в различных системах имеет, очевидно, различные координаты. Множество точек (в частности, прямая, окружность) в разных системах координат задается различными уравнениями. Выясним, как преобразуются координаты точек плоскости при переходе от одной координатной системы к другой. Ограничимся случаем ортогональных систем.
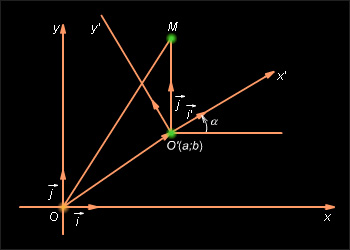
Пусть
на плоскости заданы две прямоугольные
системы координат:
![]() и
и
![]() (см.
рис. 11.3.2).
(см.
рис. 11.3.2).
|
Рисунок 11.3.2 |
Первую
систему с началом в точке O и базисными
векторами
![]() и
и
![]() назовем
старой, вторую, с началом в точке O' и
базисными векторами
назовем
старой, вторую, с началом в точке O' и
базисными векторами
![]() и
и
![]() –
новой. Положение новой системы относительно
старой будем считать известным: пусть
точка O' в старой системе имеет координаты
–
новой. Положение новой системы относительно
старой будем считать известным: пусть
точка O' в старой системе имеет координаты
![]() а
вектор
образует
с вектором
угол
α, который отсчитывается в направлении
против движения часовой стрелки от
направления, задаваемого вектором
а
вектор
образует
с вектором
угол
α, который отсчитывается в направлении
против движения часовой стрелки от
направления, задаваемого вектором
![]()
Рассмотрим произвольную точку M. Обозначим ее координаты в старой системе через (x, y), в новой – через (x', y'). Установим связь между старыми и новыми координатами точки M. Из рис. 11.3.2 по правилу треугольника имеем
|
Разложим
векторы
![]() и
и
![]() по
базису
по
базису
![]() а
вектор
а
вектор
![]() –
по базису
–
по базису
![]()
|
Равенство перепишется в виде:
|
Новые
базисные векторы
![]() и
и
![]() можно
разложить по старым базисным векторам
можно
разложить по старым базисным векторам
![]() следующим
образом:
следующим
образом:
|
Подставив найденные выражения для и в формулу, получим векторное равенство
|
равносильное двум числовым равенствам:
|
Эти формулы дают искомое выражение для старых координат через новые координаты x' и y'. Для того чтобы найти выражение для новых координат через старые, достаточно решить систему уравнений относительно неизвестных x' и y'.
Если меняется только начало координат, а направления осей остаются прежними, то, полагая в формулах α = 0, получаем
|
Эти формулы кратко называют формулами переноса.
Если начало координат остается прежним, а оси поворачиваются на угол α, то, полагая в формулах a = b = 0, получим
|
Эти формулы называются формулами поворота.

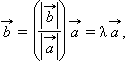
 Если векторы
и
противоположно
направлены, аналогично заключаем, что
Если векторы
и
противоположно
направлены, аналогично заключаем, что
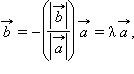
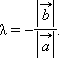 Теорема доказана.
Теорема доказана.
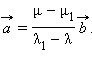 На
основании теоремы 11.7 и замечания 11.1
получаем, что векторы
и
коллинеарны.
Но это противоречит условию
неколлинеарности этих векторов.
Показанное противоречие доказывает
единственность представления. Теорема
доказана.
На
основании теоремы 11.7 и замечания 11.1
получаем, что векторы
и
коллинеарны.
Но это противоречит условию
неколлинеарности этих векторов.
Показанное противоречие доказывает
единственность представления. Теорема
доказана.
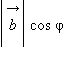 и
и
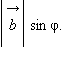 По
определению
По
определению