Білет №1

1.Властивості двовимірної щільності розподілу ймовірностей вв (х,у).

Харак-кою системи НВВ є щільність ймовірностей. Для визначення щільності ймовірностей системи двоз НВВ (Х,У) застосовується ф-ла:

P(a<x<b, c<e<d)=F(b,d)+F(a,c)-F(a,d)-F(b,c)

Властивості f(x,y):

1.Ф-ція f(x,y)>=0, оскільки F(x,y)є неспадною відносно аргументів х,у.

2.Умова нормування системи двох НВВ (Х,У) така:

3.Йм-сть розміщення с-ми змінних х,у в області

обчислюється так

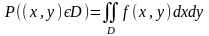
Йм-сть розміщення с-ми змінних х,у в прямокутні області D = (a<x<b, c<y<d)

4. Ф-ція розподілу йм-стей с-ми двох змінних визнач

з рів-ня:

5.Якщо Ω={a<x<b,c<y<d}, то

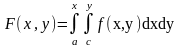
2.Емпірична ф-ція розподілу(комулята).

При побудові комуляти F(x) інтервального статистичного розподілу вибірки за основу береться припущення, що ознака на кожному частинному інтервалі має рівномірну щільність йм-сті. Тому комулята матиме вигляд ламаної лінії, яка зростає на кожному частковому інтервалі і наближається до 1.

Білет №2

1.Умовне математичне сподівання (х,у)

Для умовного закону ДВВ Х при фіксованому значенні У=у_і має виконуватись умова нормування:

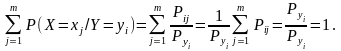
Числові хар-ки цього закону := умовними. Умовне мат сподівання:

Для уовного закону ДВВ У при фіксованому значенні Х=х_і має виконуватись умова нормування:

Умовне мат сподівання:

2.Варіаційний ряд розподілу ВВ Х.

Результати вибірки – реалізації ВВ – позначаємо відповідно через х₁, ,х_n. Розмістивши ці числа в порядку зростання і записавши частоти n_i, з якими зустрічаються ці значення, дістанемо варіаційний або статистичний ряд. На підставі такого ряду можна побудувати статистичну фун-ю розподілу:

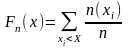
Статистичний ряд графічно подається полігоном розподілу. Щоб його побудувати, на осі абсцис відкладають значення реалізації, а на осі ординат– відповідні їм частоти (відносні частоти). Здобуті точки сполучають відрізками прямих.

Білет №3

1.Дисперсія нвв х.

Для визначення дисперсії розглядають відхилення ВВ Х від свого мат сподівання (Х-М(Х)). Мат спод такого відхилення ВВ Х завжди =0. Дисперсією ВВ Х називається мат спод квадрату відхилення ВВ Х від її мат спод. D(X)=M(X-M(X))² . Для НВВ:

2.Гістограма.

Гістограма частот являє собою фігуру, яка складається з прямокутників, кожний з яких має основу h і висоту n_i 1/n. Гістограма відносних частот є фігурою, що складається з прямокутників, кожен з яких має основу завдовжки h і висоту, що дорівнює W_i 1/n.

Білет №4

1. Функція розподілу йм-тей та її властивості.

Закон розподілу йм-тей можна подати ще в одній формі, яка придатна ідля ДВВ і для НВВ, а саме як ф-ю розподілу йм-тей ВВ F(x), так звану інтегральну ф-ю.Ф-єю розподілу ВВ Х наз Ф-я F(x), що виражає для кожного х йм-ть того, що ВВ Х прийме значення строго менше х. F(x)=Р(Х<х).Властивості: 1. 0<=F(x)<=1 (невд”ємна і обмежена). 2. F(x)- неспадна. 5.P(x₁<=X<x₂)=F(x₂)-F(x₁).