1. Постановка задачі

    2. Метод Ейлера

    3. Метод Рунге-Кутта

    4. Багатокроковий метод Адамса

    5. Багатокроковий метод Мілна

Багато інженерних задач приводять до необхідності знаходження розв`язку диференціального рівняння, що задовольняє певним початковим умовам. Однак одержати точне розв`язання диференціального рівняння вдається лише в певних спеціальних випадках, але навіть тоді часто одержують вираз, що містить шукану функцію в неявному вигляді, що затрудняє його використання.

Тому в інженерній практиці приходиться користуватися наближеними методами інтегрування диференціальних рівнянь. Ці методи умовно поділяють на аналітичні, або методи побудови наближених формул, чисельні методи, коли шуканий розв`язок одержують в табличному вигляді і графічні.

Задача відшукання розв`язку диференціального рівняння при заданих початкових умовах називається задачею Коші.

Нехай задане диференціальне рівняння першого порядку у вигляді у^’=f(x,y) (1) і початкові умови у(х₀)=у₀ (2). Задача Коші полягає в тому, щоб знайти функцію у=у(х), що являється розв`язком рівняння (1) і задовільняє умови (2). Очевидно, лише в цьому випадку, коли відомо, що розв`язок задачі Коші існує і єдиний, має зміст говорити про відшукання його наближеного представлення.

Із теорії диференціальних рівнянь відомо, що якщо в деякій області D площини х0у, що містить точку (х₀;у₀), функція f(x,y) неперервна і має неперервну частинну похідну , то в деякому околі точки х₀ існує єдина функція у=у(х), що являється розв`язком рівняння (1) і задовольняє початкові умови (2) (теорема Коші).

Аналогічно ставиться задача Коші для :

а) диференційованого рівняння другого порядку, представленого у вигляді у^”=f(x,y,y^’) (3), при початкових умовах у(х₀)=у₀, у^’(x₀)=y^’₀. Потрібно знайти функцію у=у(х), що являється розв`язком рівняння (3) і задовольняє умовам (4).

б) системи двох диференціальних рівнянь першого порядку, представленої у вигляді

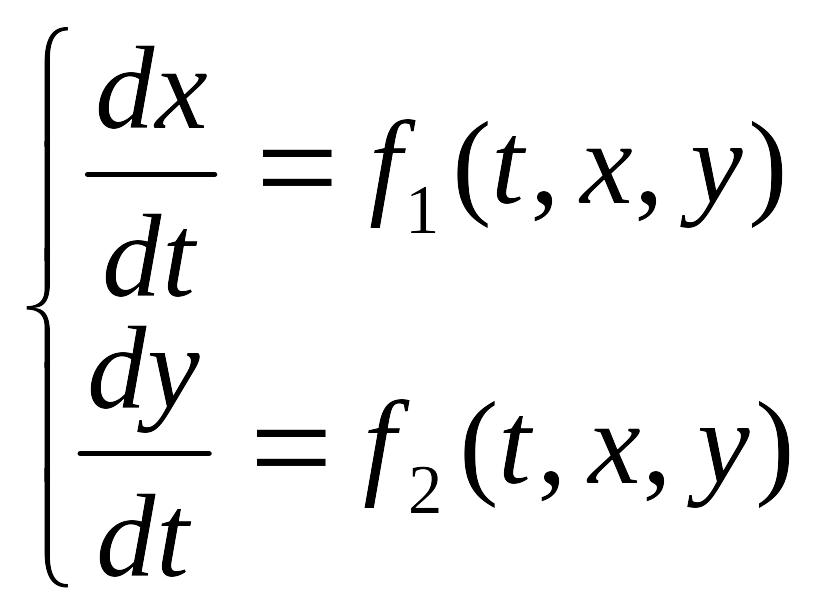(5) при початкових умовах x(t₀)=x₀, y(t₀)=y₀. (6)

Треба знайти функції х=х(t), y=y(t), що являються розв`язком системи (5) і задовольняє умови (6);

в) системи трьох диференціальних рівнянь першого порядку, представленої у вигляді

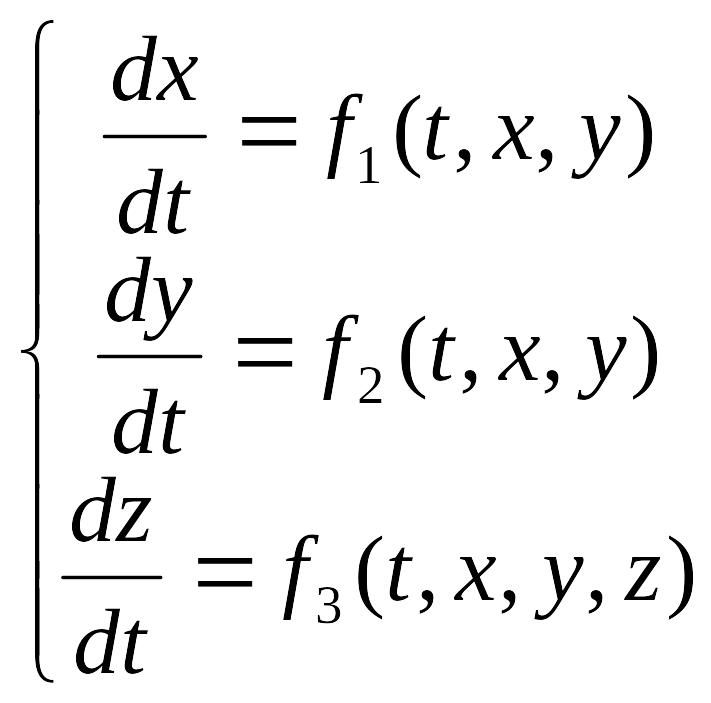(7)

при початкових умовах.

Метод Ейлера для розв’язання диференціального рівняння першого порядку. Розглянемо задачу відшукання наближеного розв’язку диференціального рівняння у^’=f(x,y) (1) при початкових умовах у(х₀)=у₀ (2) на відрізку [x₀;x₀+a].

При відшуканні чисельного розв’язку задачі (1), (2) відрізок [x₀;x₀+a] розбивають на n рівних частинних відрізки, довжина яких h= . Число h називається кроком інтерполяції (чи просто кроком). Наближене значення шуканої функції у=у(х) відшукується в точках поділу х₀, х₁=х₀+h, x₂=x₁+h, …, x_n=x_n-1+h=x₀+a.

Метод Ейлера являється найбільш простим із всіх методів чисельного розв`язання диференціальних рівнянь. Геометрично він полягає в тому, що на малому відрізку [x;x+h] інтегральна крива у=у(х) диференціального рівняння (1) заміняється відрізком її дотичної в точці (х;у(х)). Так, на першому відрізку [x₀;x₁] із точки М₀(х₀;у₀) проводимо дотичну до інтегральної кривої, тобто пряму з кутовим коефіцієнтом у^’(x₀)=f(x₀,y₀), рівняння якої у-у₀=f(x₀,y₀)(x-x₀). Визначаємо точку перетину прямої з прямою, паралельною осі оу і та що проходить через точку х₁, тобто з прямою х=х₁. Підставивши х=х₁ в рівняння дотичної, одержимо у₁=у₀+f(х₀,у₀)(х-х₀)=y₀+f(х₀,у₀)h. Число у₁ вважають наближеним значенням розв’язку в точці х₁. Повторимо ту саму процедуру на відрізку [x₁;x₂]. А іменно, побудуємо дотичну до інтегральної кривої, що проходить через точку М₁(х₁;у₁), тобто пряму з кутовим коефіцієнтом у^’(x₁)=f(x₁,y₁), рівняння якої у-у₁=f(x₁,y₁)(x-x₁), і відшукуємо ординату у₂ точки М₂(х₂;у₂), що лежить на прямій у₂=у₁+f(x₁,y₁)(x₂-x₁)=y₁+f(x₁,y₁)h. Число у₂ вважається наближеним значенням розв’язання в точці х₂.

Продовжуємо цю процедуру до тих пір, поки не отримаємо відрізок [x_n-1;x_n=x₀+a] і не визначемо у_n=y_n-1+f(x_n-1,y_n-1)h – ординату точки М_n(x_n;y_n). Число у_n вважаємо наближеним значенням розв’язку в точці х_n.

З’єднавши точки М₀,М₁,...,М_n, одержимо ламану, яка наближено представляє інтегральну криву диференціального рівняння. Цю ламану прийнято називати ламаною Ейлера. Рівнянням її є кусково-лінійна функція, яка являється наближеним розв’язанням задачі (1), (2) на відрізку [x₀;x₀+a].

Метод Рунге-Кутта найбільш часто застосовується при чисельному розв’язанні задачі Коші і дозволяє одержувати наближення високої точності. Геометрично цей метод для задачі Коші (нехай задане диференціальне рівняння першого порядку у вигляді у^’=f(x,y) (1) і початкові умови у(х₀)=у₀ (2). Задача Коші полягає в тому, щоб знайти функцію у=у(х), що являється розв`язком рівняння (1) і задовільняє умови (2)) також полягає в тому, що на малому відрізка [х; x+h] інтегральна крива y=y(x) рівняння (1) заміняється відрізком прямої, що проходить через точку (х;у=у(х)). Однак в основу методу покладений біль тонкий, ніж в методі Ейлера, підхід до визначення напряму цього відрізку прямої.

Нехай відрізок [x₀;x₀+a] розділений на n рівних частин точками x₀, x₁,...,х_к, х_к+1,..., х_n=x₀+a(x_k+1-x_k= =h) і визначені наближені значення у₀,...,у_к розв’язку диференціального рівняння відповідно в точках x₀,..., x_к. Переходимо до відрізку[x_k; x_k+1] і до відшукання у_к+1. Визначаємо а_1к=f(x_k;y_k) – напрямок дотичної до інтегральної кривої в точці M_k(x_k;y_k), і точку перетину прямих y-y_k=а_1к(x-x_k) і х=х_к+ ,тобто точку N . Знаходимо напрям дотичної в точці N : а_2к=f і з точки М_к проводимо пряму з кутовим коефіцієнтом а_2к: y-y_k=а_2к(x-x_k) до перетину з прямою х=х_к+ . Одержимо точку N . Знаходимо напрям дотичної в точці N : а_3к=f і з точки М_к проводимо пряму з кутовим коефіцієнтом а_3к: y-y_k= а_3к (x-x_k) до перетину з прямою х=х_к+h. Одержуємо точку М (х_к+h,y_k+а_3кh). Далі визначаємо напрям дотичної в точці М : а_4к=f . В кінці напрям відрізка ламаної, що представляє наближений розв’язок задачі, покладають рівним а_к=1/6(а_1к+2а_2к+2а_3к+а_4к) і проводимо з точки M_k пряму y-y_k=а_к(x-x_k) до перетину з прямою х=х_к+h в точці M_k+1(x_k+1;y_k+1), де y_k+1=у_к+а_кh вважають наближеним значенням розв’язку в точці x_k+1=х_к+h.

Метод будемо називати однокроковим, якщо для отримання розв’язку на к-тому кроці будемо використовувати лише розв’язок отриманий лише на к-тому кроці. Якщо для отримання розв’язку на к-тому кроці використовуватимемо декілька попередніх кроків (найчастіше чотири), то метод будем називати багатокроковим.

Метод Адамса є багатокроковим і використовує розв’язки у чотирьох точках, які знайдені за допомогою однокрокового методу. Метод Адамса грунтується на принципі знаходження значення у_і+1, з його допомогою обчислюють f_i+1 і використовуючи f_i+1 і ще декілька попередніх розв’язків у точках х_і, х_і-1,х_і-2 проводять уточнення у_і+1. Для методу Адамса формула має вигляд:

у_і+1=у_і+ (55*f_i-59*f_i-1+37f_i-2-9f_i-3), де f_i=f(x_i,y_i).

За даним у_і+1 обчислюють f_i+1=f(x_i+1,y_i+1) і уточнюють у_і+1:

у_і+1=у_і+ (9*f_i+1+19*f_i-5f_i-1+f_i-2). Дана формула отримується з використанням інтерполяційного многочлена Ньютона.

Метод Мілна являється багатокроковим методом четвертого порядку. Для його початку необхідно знайти будь-яким однокроковим методом чотири значення шуканого розв’язку у₀, у₁, у₂, у₃. Подальші обчислення проводяться по схемі:

1. 1.    По чотирьох попередніх точках передбачаються наступні значення у_і+1:

У_і+1^{наближене}=у_і-3+ h(2f_i-f_i-1+2f_i-2), де f_i=f(x_i,y_i); (i=3,4,5,…)

2. 2.    Обчислюємо значення правої частини рівняння f_i+1^{наближене}=f(x_i+1;y_i+1^{наближене}).

3. 3.    Коректуємо значення у_і+1:

у_і+1^{уточнене}=у_і-1+h/3(f_i-1+4f_i+f_i+1^{наближене}), (і=3,4,...)

Гранична абсолютна похибка значення у_і в методі Мілна рівна Е_і=1/29|y_i^{наближене}-у_і^{уточнене}|

55