1. Постановка задачі

 2. Формули прямокутників

• лівих

• правих

• середніх

  3. Формула трапеції

 4. Формула Сімпсона

 5. Формула Монте - Карло

 6. Графічне інтегрування 

Нехай функція f(x) задана на деякому відрізку [a;b]. Розглянемо задачу обчислення її визначеного інтеграла 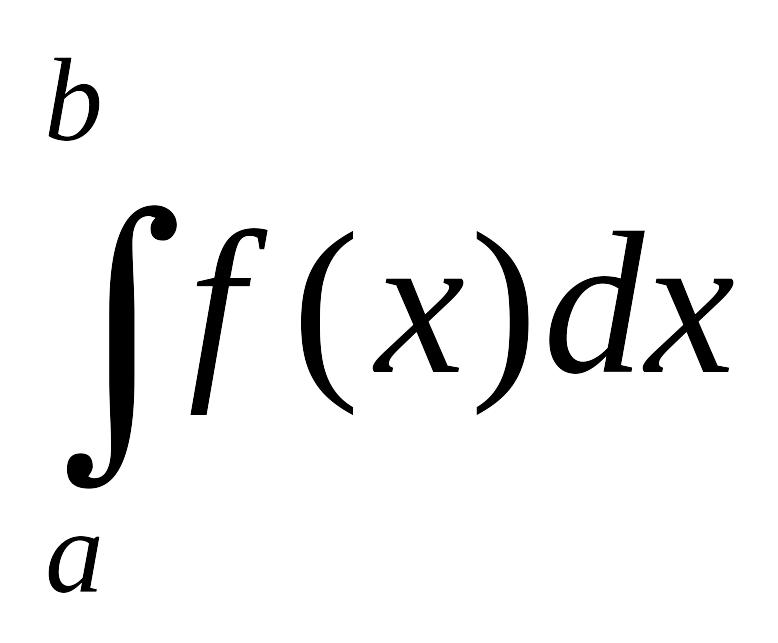. Якщо для f(x) відома первісна F(x), то інтеграл може бути обчислений точно по основній формулі інтегрального числення – формулі Ньютона-Лейбніца

Однак первісна лише для вузького классу функцій виражається через елементарні функції, причому нерідко її відшукання зв`язане з дуже громісткими обчисленнями. Крім того, можлива ситуація, коли підінтегральна функція задана не аналітично, а таблично чи графічно. Тому для обчислення визначеного інтеграла часто приходиться застосовувати різні наближені формули. Досить просто ці формули можна одержати, виходячи з геометричного змісту визначеного інтегралу: якщо f(x) на [a;b], то - площа криволінійної трапеції, обмеженої відрізком [a;b] осі ох, кривою у=f(x) і прямими х=а, х=b. При наближеному обчисленні криволінійну трапецію заміняють фігурою, обмежену тим же відрізком [a;b], площа якої обчислюється значно простіше. Звідси одержують наближену формулу =S , яку використовують для обчислення лише тоді, коли можна оцінити її похибку.

В дальнішому розглядається функція f(x) для х [a;b], але одержані результати будуть вірні для будь-якої інтегруючої на [a;b] функції.

Ідея формули прямокутників заключається в тому, що на малому відрізку [x ;x +h] площа криволінійної трапеції приблизно рівна площі прямокутника з основою [x ;x +h] і висотою, що рівна ординаті в якійсь точці [x ;x +h], тобто

.

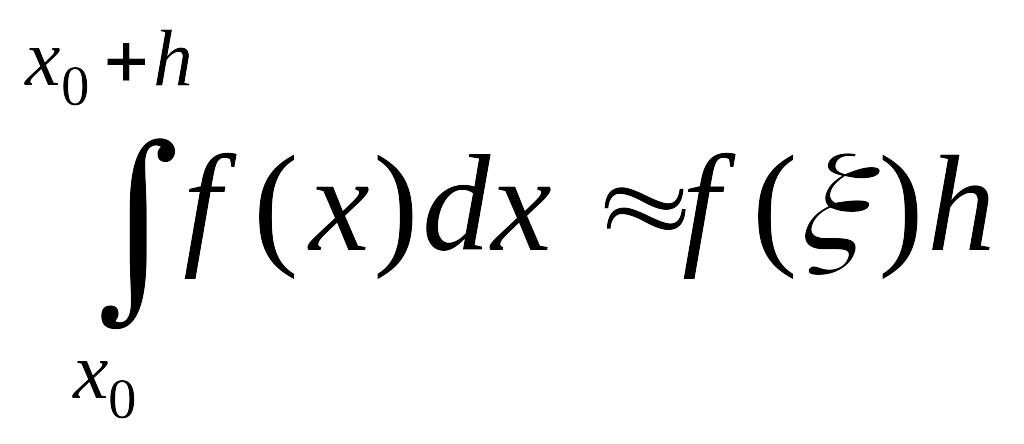В залежності від того, яку точку відрізка [x ;x +h] вибирають в якості , і одержимо різновиди формули прямокутників.

Розіб`ємо відрізок [a;b] на n різних частин точками де h=

На кожному частинному відрізку [ ] замінимо відповідну криволінійну трапецію на прямокутник, висоту якого можна визначити по різному.

Формули лівих прямокутників. Якщо вибрати в якості висоти прямокутника на кожному з відрізків [ ] (і= ) ординату в лівому кінці, тобто , то криволінійна трапеція заміниться на ступіньчасту фігуру, площа якої можна прийняти за площу трапеції. Відповідно,

S , =S =h .

 

Одержану формулу називають формулою лівих прямокутників.

Ідея формули прямокутників заключається в тому, що на малому відрізку [x ;x +h] площа криволінійної трапеції приблизно рівна площі прямокутника з основою [x ;x +h] і висотою, що рівна ординаті в якійсь точці [x ;x +h], тобто

.

В залежності від того, яку точку відрізка [x ;x +h] вибирають в якості , і одержимо різновиди формули прямокутників.

Розіб`ємо відрізок [a;b] на n різних частин точками де h=

На кожному частинному відрізку [ ] замінимо відповідну криволінійну трапецію на прямокутник, висоту якого можна визначити по різному.

Формула правих прямокутників. Якщо в якості висоти прямокутника вибрати ординату правого кінця частинного відрізка, тобто висота прямокутника на відрізку [ ] рівна , i=( ), то для наближеного обчислення інтеграла одержимо формулу правих прямокутників: S , =S =h .

Ідея формули прямокутників заключається в тому, що на малому відрізку [x ;x +h] площа криволінійної трапеції приблизно рівна площі прямокутника з основою [x ;x +h] і висотою, що рівна ординаті в якійсь точці [x ;x +h], тобто

.

В залежності від того, яку точку відрізка [x ;x +h] вибирають в якості , і одержимо різновиди формули прямокутників.

Розіб`ємо відрізок [a;b] на n різних частин точками де h=

На кожному частинному відрізку [ ] замінимо відповідну криволінійну трапецію на прямокутник, висоту якого можна визначити по різному.

Формула середніх прямокутників. Висотою прямокутника, побудованого на частинному відрізку, вважають ординату, взяту в середній точці відрізка, тобто . Тоді S , =S =h .

Формула трапеції заснована на тому, що на відрізку [x ;x +h] дугу кривої у=f(x) заміняють хордою, що стягує кінці цієї дуги, тобто проводять лінійне інтерполювання функції у=f(x). При цьому площу криволінійної трапеції заміняють площою трапеції з основами f(x ) і f(x +h) і висотою h, відповідно, Звідси, щоб обчислити , розіб`ємо відрізок [a;b] на n рівних частинних відрізки, так що крок .

 

Проведемо через точки поділу ординати і замінимо дану криву ламаною, відрізки якої з`єднують кінці двух сусідніх ординат. Криволінійна трапеція при цьому заміниться на фігуру, що складається з n трапецій, висоти яких h, а основи – ординати , i=( ) в точках поділу. Площа такої фігури виражається формулою , а для обчислення інтеграла маємо формулу =S =h , яку називають формулою трапеції.

Метод Сімпсона .

Спосіб наближеного обчислення визначеного інтеграла по формулі Сімпсона заснований на тому, що на відрізку [x ;x +2h] дугу кривої у=f(x) заміняють дугою квадратичної параболи, що проходить через точки А(х ;f(x )), В(х +h;f(x +h)), C(х +2h;f(x +2h)), тобто проводять квадратичне інтерполювання функції у=f(x). Тоді за наближене значення площі криволінійної трапеції приймають площу параболічної трапеції, яка має ту саму основу [x ;x +2h] і обмежена зверху дугою параболи. Для того, щоб скласти рівняння цієї параболи, використаємо першу інтерполяційну формулу Н`ютона. Складемо многочлен другої степені по трьох вузлах інтерполяції: х , х =x +h, х =x +2h. Одержимо .

Перетворимо цей вираз. Так як х =x +h, то (х-x )*(х-х )=(х-x )*((х-x )-h)=(х-x ) -(х-x )*h i . Площа параболічної трапеції S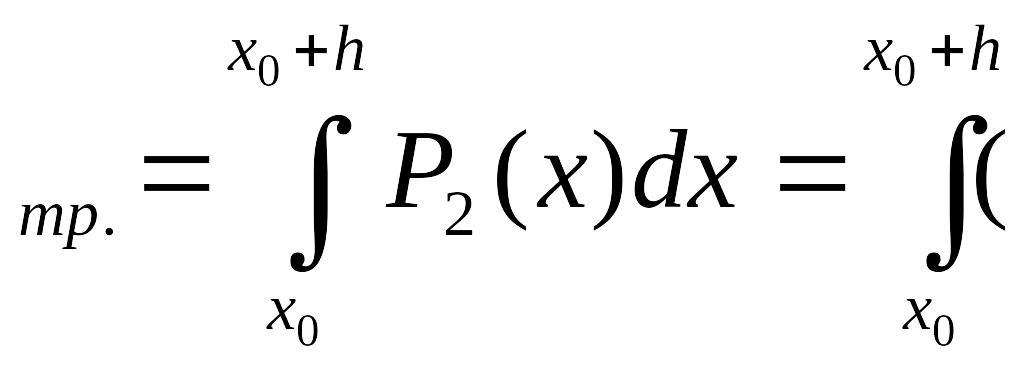

. Якщо ввести позначення - ордината початку відрізка, - ордината кінця відрізка, то одержана формула матиме вигляд S ) (1), де .

 

Розділимо тепер відрізок [a;b] на n их частин, причому ввазатимемо n-парним числом, тобто n=2m, тоді .

Нехай - точки поділу. Прведемо ординати в цих точках .З`єднаємо кінці кожних трьох сусідніх ординат дугами парабол, тобто на відрізках криву дугами парабол. Застосуємо до кожного з відрізків формулу (1). Тоді

, звівши подібні доданки, одержимо

(2)

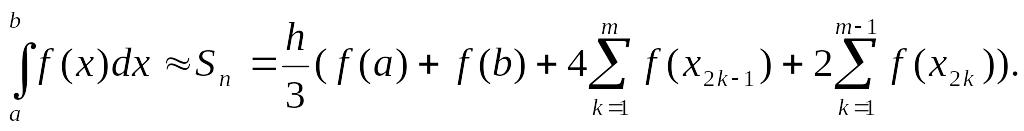Формулу (2) називають параболічною формулою чи формулою Сімпсона. Розглянемо задачу відшукання наближеного значення по формулі (2) і оцінимо похибку одержаного наближення. Для контролю задамо число Е>0 – точність шуканого наближення. Метод розв`язання задачі полягає в наступному. Значення S послідовно обчислюються по фомулі (2) при n=2,4,8,...,2 ,..., тобто обчислюються наближення . Після наступного обчислення (n>2) визначається похибка одержаного наближення: . Якщо , то наближення задовільняє заданій точності. Обчислення закінчене і = - наближене значення визначеного інтеграла, при заданому Е>0. В інакшому випадку обчислення повторюються.

Метод Монте-Карло.

Постановка задачі: ми маємо криволінійну трапецію, яка обмежена y=f(x), x=a, x=b і відрізком [a;b]. Необхідно знайти таку фігуру, яка повністю вміщає в себе криволінійну трапецію і достатньо просто знайти площу цієї фігури. Позначимо через S – площу фігури, яка включає криволінійну трапецію. Через S - площу криволінійної трапеції. Через N –кількість точок, які ми будемо вкидати у фігуру площі S. А через N - кількість точок, які попадуть у криволінійну трапецію. Тоді справедливе співвідношення . Звідси .

 

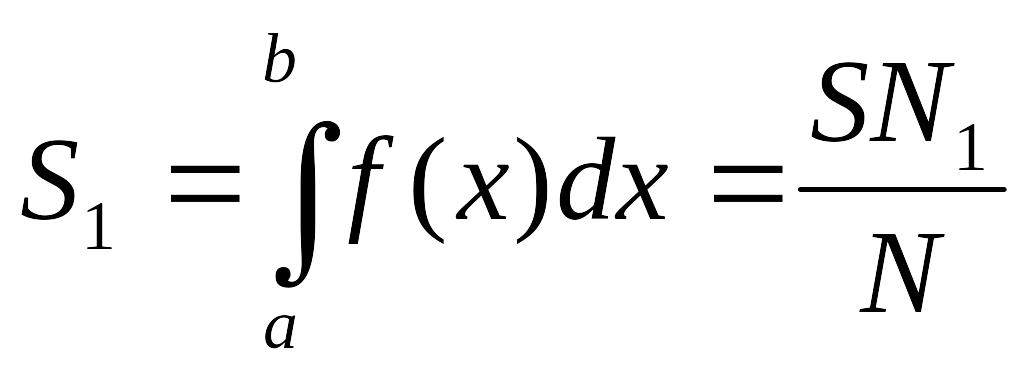Зауваження 1: В оптимальному випадку відшуковується max значення функції y=f(x) на відрізку [a;b] і обчислюється площа прямокутника зі сторонами :

1. 1)    сторона b-a,

2. 2)    сторона max(f(x)).

Зауваження 2: Результат обчислення не залежить від вигляду і площі фігури, яка включає криволінійну трапецію.

Зауваження 3: Для складання програми необхідно використати генератор випадкових чисел. Перед цим необхідно активізувати його за допомогою стрічечки рандомайс.

Графічного інтегрування.

Наближене обчислення інтеграла методом графічного інтегрування застосовується тоді, коли підінтегральна функція задана графічно. Нехай на [a;b] задана неперервна крива, рівняння якої y=f(x). На основі теореми про середнє для визначеного інтеграла існує така точка [a;b], що

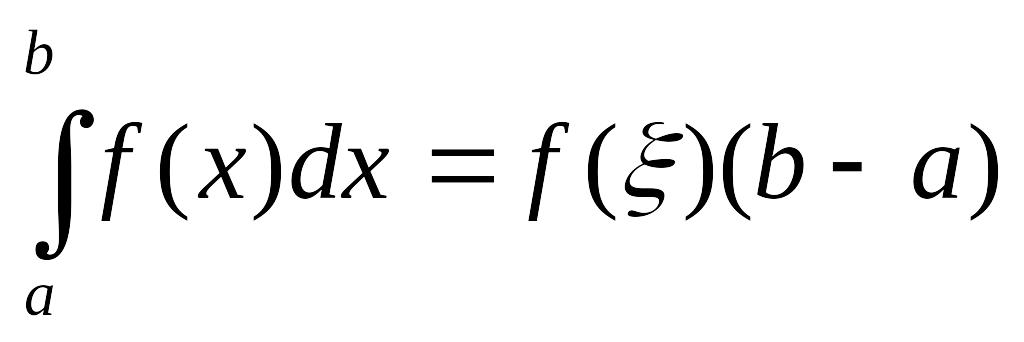. Геометрично це означає, що площа криволінійної трапеції чисельно рівна площі прямокутника з основою [a;b] і висотою f( ). Розглянемо криволінійну трапецію і проведемо горизонтальну пряму приблизно так, щоб одержати потрібний прямокутник. Абсцисами точок перетину прямої і кривої будуть ті точки , про яких згадується у теоремі про середнє. Відкладемо на осі ох зліва від початку координат одиничний відрізок ОР і продовжимо проведену горизонтальну пряму до перетину з віссю ординат (якщо а<0, то краще спочатку зліва від а провести вертикальну пряму і при дальніших діях замінити вісь оу цією прямою). Нехай пряма перетне вісь оу в точці Q, тоді ОQ =f( ). З`єднаємо точки Р і Q і з точки а проведемо пряму аМ, паралельно РQ, до перетину в точці М з вертикаллю, проведеною з точки b. Покажемо, що bМ= , тобто величина побудованого відрізка чисельно рівна значенню визначеного інтеграла. Дійсно, . Звідси

 

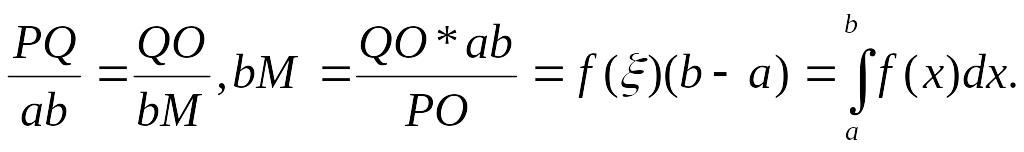
Зауваження: Функція f(x)>0. Однак одержаний результат має місце для будь-якої неперервної на [a;b] функції y=f(x). Наприклад, функція f(x) міняє знак на [a;b]. Заштриховані площі на рисунку 2 приблизно рівні. Оскільки площа частини криволінійної трапеції, розміщеної нище осі ох, більша, то буде від`єним. Проводячи попередні побудови, одержимо відрізок bM, величина якого від`ємна і тут bM= .

На основі проведеної побудови і проводиться графічне інтегрування.

Лекції: Наближене диференціювання.

 

1. Постановка задачі наближеного диференціювання

2. Наближене диференціювання за допомогою      інтерполяційного многочлена Ньютона

3. Графічне диференціювання

 

Чисельним диференціювання користуються для відшукання похідної функції, а також для наближеного обчислення похідної аналітично заданої функції, безпосереднє диференціювати яку тяжко.

Для відшукання похідної функції y=f(x) здійснюють інтерполюваня функції на розглядуваному відрізку [a;b] многочленом P_n(x) і його похідну приймають за похідну функції, тобто покладають

f^’(x)=P_n^’(x), a x b (1).

Аналогічно можна поступати і при знаходженні похідних вищих порядків, хоча для похідних порядку вище другого таку процедуру зазвичай не застосовують. Це зв’язано з тим, що похибка наближеної формули (1) мало зв’язана з похибкою інтерполювання. Дійсно, геометрично очевидно, що якщо ординати f(x₁) i P_n(x) кривих y=f(x) i y=P_n(x) в точці х₁ мало відрізняються одна від другої, то це не веде за собою незначної відмінності їх похідних f^’(x₁) i P_n^’(x₁) – кутових коефіцієнтів дотичних до цих кривих (рис). З зростанням порядку похідної точність чисельного диференціювання різко падає.

Для знаходження похідної f^’(x) функції f(x), заданої таблицею з рівностоящими вузлами, використаємо многочлен Ньютона, представлений першою формулою, якщо х ближче до х₀, чи другою, якщо х ближче до х_n. Тоді із P_n(x)=P_n(x₀+th)=y₀+ ,

враховуючи t= , одержимо

P_n^’(x)=(P_n(x₀+th))_x^’=(P_n)^’_t*t_x^’= ,

P_n^”(x)=(P_n^’(x_n+th))_x^’=(P_n^’)_t*t_x^’= .

Аналогічно із P_n(x)=P_n(x_n+th)=y_n+ ,

враховуючи t= , одержимо

P_n^’(x)=(P_n(x_n+th))_x^’=(P_n)^’_t*t_x^’= ,

P_n^”(x)=(P_n^’(x_n+th))_x^’=(P_n^’)_t*t_x^’= .

Відмітимо, що за х₀ чи х_n можна прийняти будь–який проміжний вузол таблиці, тому зазвичай вибирають ближчий до х табличне значення аргументу.

Формули чисельного диференціювання значно спрощуються, якщо похідна відшуковується у вузлі інтерполяції, наприклад в точці х_k . Прийнявши тоді х_k за х_0, одержимо t=0, а із формул одержуємо

P_n^’(x₀)= ,

P_n^”(x)= .

Чисельним диференціювання користуються для відшукання похідної функції, а також для наближеного обчислення похідної аналітично заданої функції, безпосереднє диференціювати яку тяжко.

Для відшукання похідної функції y=f(x) здійснюють інтерполюваня функції на розглядуваному відрізку [a;b] многочленом P_n(x) і його похідну приймають за похідну функції, тобто покладають

f^’(x)=P_n^’(x), a x b (1).

Аналогічно можна поступати і при знаходженні похідних вищих порядків, хоча для похідних порядку вище другого таку процедуру зазвичай не застосовують. Це зв’язано з тим, що похибка наближеної формули (1) мало зв’язана з похибкою інтерполювання. Дійсно, геометрично очевидно, що якщо ординати f(x₁) i P_n(x) кривих y=f(x) i y=P_n(x) в точці х₁ мало відрізняються одна від другої, то це не веде за собою незначної відмінності їх похідних f^’(x₁) i P_n^’(x₁) – кутових коефіцієнтів дотичних до цих кривих (рис). З зростанням порядку похідної точність чисельного диференціювання різко падає.

Для знаходження похідної f^’(x) функції f(x), заданої таблицею з рівностоящими вузлами, використаємо многочлен Ньютона, представлений першою формулою, якщо х ближче до х₀, чи другою, якщо х ближче до х_n. Тоді із P_n(x)=P_n(x₀+th)=y₀+ ,

враховуючи t= , одержимо

P_n^’(x)=(P_n(x₀+th))_x^’=(P_n)^’_t*t_x^’= ,

P_n^”(x)=(P_n^’(x_n+th))_x^’=(P_n^’)_t*t_x^’= .

Аналогічно із P_n(x)=P_n(x_n+th)=y_n+ ,

враховуючи t= , одержимо

P_n^’(x)=(P_n(x_n+th))_x^’=(P_n)^’_t*t_x^’= ,

P_n^”(x)=(P_n^’(x_n+th))_x^’=(P_n^’)_t*t_x^’= .

Відмітимо, що за х₀ чи х_n можна прийняти будь–який проміжний вузол таблиці, тому зазвичай вибирають ближчий до х табличне значення аргументу.

Формули чисельного диференціювання значно спрощуються, якщо похідна відшуковується у вузлі інтерполяції, наприклад в точці х_k . Прийнявши тоді х_k за х_0, одержимо t=0, а із формул одержуємо

P_n^’(x₀)= ,

P_n^”(x)= .

Суть графічного диференціювання полягає в тому, щоб по графіку функції, заданому на деякому відрізку [a;b], будується приблизно графік її похідної. Ця побудова основана на геометричному змісті похідної і по формулі Лагранжа скінчених приростів.

Нехай на малому відрізку [x₀;x₀+ x] заданий графік функції y=f(x). Із формули скінчених приростів слідує, що

f^’( )= ,

де х₀< <x₀+ x. Геометрично вираз, що стоїть справа, це тангенс кута нахилу хорди АВ, а розміщений зліва кутовий коефіцієнт дотичної до цієї точки Є(x₀;x₀+ x). Якщо x мале, то в якості можна взяти точку, що лежить посередині [x₀;x₀+ x], тобто =х₀+ , тоді одержуємо наближену рівність f^’(х₀+ ) .

Для відшукання похідної в точці х₀+ треба знайти тангенс кута нахилу хорди АВ. Для цього проведемо слідуючи побудови. Від точки О (або від любої другої точки зовні відрізка [x₀;x₀+ x]) вліво відкладемо одиничний відрізок ОК і проведемо KD||AB. Величина відрізка OD=OK*tg , де =<DKO=<BAC. Відповідно, OD=f^’(х₀+ ). Проведемо DN паралельно осі ох. Тоді точка N, що відповідає абсцисі х₀+ , буде мати ординатою f^’(х₀+ ), тобто це точка графіка похідної функції f(x).

Нехай тепер функція f(x) задана на відрізку [a;b]. Відрізок [a;b] розіб’ємо на n частинних відрізки, не обов’язково рівних між собою, але так, щоб на кожному із них функція вела себе монотонно. На кожному частинному відрізку проведемо побудови, аналогічні описаним вище для відрізка [x₀;x₀+ x]. В кінці побудовані точки, аналогічні точці N, з’єднуємо ламаною, яка приблизно представляє графік похідної заданої функції f(x).

Лекції: Наближені методи розв'язування звичайних диференціальних рівнянь