2.Точечные оценки параметров распределения.

1. Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 8, 9, , 12. Если несмещенная оценка математического ожидания равна 10, то выборочная дисперсия будет равна …(2,5).

2. Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна …(6,38)

3. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …(11,25).

4. Из генеральной совокупности извлечена выборка объема : 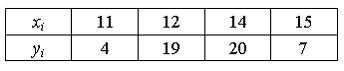Тогда несмещенная оценка математического ожидания равна …(13,14)

5. По выборке объема  найдена выборочная дисперсия . Тогда исправленное среднее квадратическое отклонение равно …(2)

6. Из генеральной совокупности извлечена выборка объема : Тогда выборочное среднее квадратическое отклонение равно …

7.Если все варианты  исходного вариационного ряда увеличить в два раза, то выборочная дисперсия  … (увеличится в четыре раза)

8. Из генеральной совокупности извлечена выборка объема : Тогда выборочная дисперсия равна …(0,84)

9. Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 2,1; 2,3; ; 2,7; 2,9. Если несмещенная оценка математического ожидания равна 2,48, то  равно …(2,4)

10. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна …(0,13)

3.Элементы корреляционного анализа.

1. Выборочное уравнение прямой линии регрессии  на  имеет вид . Тогда выборочный коэффициент корреляции может быть равен …(0,82)

2. При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции  и выборочные средние квадратические отклонения . Тогда выборочный коэффициент регрессии  на    равен …

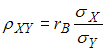
3. Выборочное уравнение прямой линии регрессии  на  имеет вид . Тогда выборочный коэффициент корреляции может быть равен … (– 0,67)

4. Выборочное уравнение прямой линии регрессии  на  имеет вид . Тогда выборочное среднее признака  равно …

5. Выборочное уравнение прямой линии регрессии  на  имеет вид , а выборочные средние квадратические отклонения равны: . Тогда выборочный коэффициент корреляции  равен …(0,15)

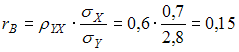
6. Выборочное уравнение прямой линии регрессии  на  имеет вид . Тогда выборочный коэффициент регрессии равен …(– 1,5)

7. Выборочное уравнение прямой линии регрессии  на  имеет вид . Тогда выборочный коэффициент корреляции может быть равен …

8. Выборочное уравнение прямой линии регрессии  на  имеет вид . Тогда выборочное среднее признака  равно …

9. При построении выборочного уравнения прямой линии регрессии  на  вычислены выборочный коэффициент регрессии , и выборочные средние  и . Тогда уравнение регрессии примет вид …

10. При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции  и выборочные средние квадратические отклонения . Тогда выборочный коэффициент регрессии Y  на  X  равен …(1,08)