Де 3. Дифференциальное и интегральное исчисление примеры

1. Непрерывность функции. Точки разрыва.

1. Точка  является точкой разрыва функции …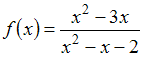 (для остальных функций х=2 не входит в область определения)

2. Для функции  точка  является точкой …(разрыва 2-го рода, т.к. предел 1/(2х-5) в точке 2,5 равен ± ∞, 3^+∞⇾∞).

3. Количество точек разрыва функции 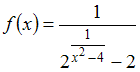 равно …(4: f(x) не существует при х²-4 =0 (х= ±2) и при 1/(х²-4)=1).

4. Для функции 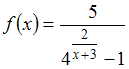 точка  является точкой … (разрыва 1-го рода, т.к. предел 2/(х+3) в точке х=-3 равен ± ∞, 4^+∞⇾∞, а f(x)⇾0, 4^-∞⇾0, а f(x)⇾-5).

5. Количество точек разрыва функции 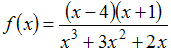 равно …(3), знаменатель не существует при х=0, х=-1 и х=-2, при этом точка х=-1 –устранимая т. разрыва.)

6. Точка разрыва функции 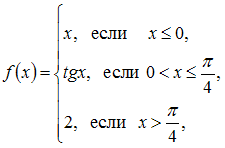 равна …

7. Количество точек разрыва функции 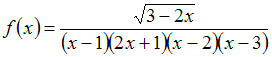 равно …(2)

Точка разрыва функции 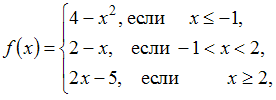 равна …(2)

2.Производные высших порядков.

1. Производная второго порядка функции  равна …

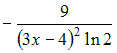
2. Значение производной второго порядка функции  при  равно …

3. Производная второго порядка функции  равна …

4. Функция  задана в параметрическом виде 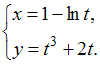  Тогда производная второго порядка функции  по переменной  имеет вид … .

5. Значение производной второго порядка функции  при  равно …(3)

6. Производная второго порядка функции  равна …

7. Производная второго порядка функции  равна …

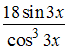
8. Производная третьего порядка функции  равна …( )

3.Методы вычисления определенного интеграла.

1. Определенный интеграл 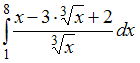 равен …(33/5)

2. Определенный интеграл 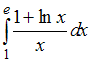 равен …(3/2) (dx/x=d(lnx))

3. Определенный интеграл 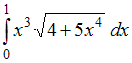 равен …(19/30) (d(4+5x⁴)=20x³dx)

4. Несобственный интеграл 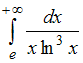 …(1/2) (dx/x=d(lnx))

5. Определенный интеграл 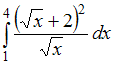 равен …

6. Определенный интеграл 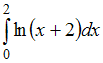 равен … (интегрирование по частям)

7. Определенный интеграл 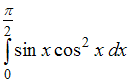 равен … .

8. Определенный интеграл 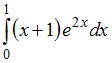 равен …

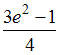
4. Приложения дифференциального исчисления фоп

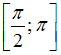1. Наименьшее значение функции на отрезке  равно …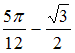 (наименьшее (наибольшее) значение выбираем среди значений функции на концах отрезка и в критических точках внутри отрезка).

2. Материальная точка движется прямолинейно по закону . Тогда ускорение точки в момент времени  равно …(0))(a(t)=x’’(t) = 3t-6, a(2)=0)/

3. Минимум функции  равен …(-13/60; f’(x)=0 при х=0, х=1 и х=-2. Смена знака производной с минуса на плюс при переходе через х=1 указывает, что это точка минимума)

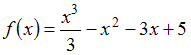4. Уравнение касательной к графику функции  в его точке с абсциссой  имеет вид … ( y-f(x₀)=f ‘(x₀)(x-x₀)) 5. Промежуток возрастания функции  имеет вид … (т.к. f’(x)<0⟹f(x)убывает, f’(x)>0⟹f(x) возрастает)

6. Промежуток убывания функции 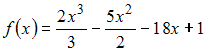 имеет вид …

7. Наибольшее значение функции на отрезке  равно …(-1)

Де 4. Векторный анализ. Примеры

1. Норма вектора в евклидовом пространстве

1. Норма вектора ,  в евклидовом пространстве со стандартным скалярным произведением равна 5 при  равном …(-2).

2 Если  и  – ортогональные векторы из евклидова пространства со стандартным скалярным произведением, такие что , , то норма вектора  равна …(5) 3. Если  и  – ортогональные векторы из евклидова пространства со стандартным скалярным произведением, такие что , , то норма вектора  равна …(10)

4. Даны векторы  и , угол между которыми равен . Тогда проекция вектора  на вектор  равна … .

5. Скалярное произведение векторов  и  равно 5, угол между векторами равен , норма вектора  равна 2. Тогда норма вектора  равна …(5)

6. Скалярное произведение векторов  и  равно 8, угол между векторами равен , норма вектора  равна 4. Тогда норма вектора  равна …(4)

7. Даны векторы  и , угол между которыми равен . Тогда проекция вектора  на вектор  равна …(3)