
- •1. Вычисление определителей.
- •3. Корень уравнения равен … (– 1)
- •7. Корень уравнения равен …(-1).
- •8. Определитель равен …(91)
- •2. Матрицы.
- •5. Матрица , где и . Тогда элемент равен …(11).
- •8. Даны матрицы и Тогда матрица имеет вид …
- •3. Системы линейных уравнений.
- •6. Фундаментальное решение может быть вычислено для системы вида …(только для однородной)
- •Де 2. Аналитическая геометрия. Примеры.
- •1.Прямоугольные координаты на плоскости.
- •2. Прямая на плоскости.
- •3. Кривые 2-го порядка.
- •4. Плоскость в пространстве.
- •Де 3. Дифференциальное и интегральное исчисление примеры
- •Непрерывность функции. Точки разрыва.
- •2.Производные высших порядков.
- •3.Методы вычисления определенного интеграла.
- •4. Приложения дифференциального исчисления фоп
- •Де 4. Векторный анализ. Примеры
- •1. Норма вектора в евклидовом пространстве
- •2. Векторное произведение векторов.
- •3. Градиент.
- •Де 5. Функциональный анализ примеры
- •Мера плоского множества
- •2. Элементы теории множеств
- •3. Отображения множеств
- •3.Дифференцирование функции комплексного переменного.
- •3. Элементы гармонического анализа.
- •4. Тригонометрический ряд Фурье.
- •Де 8. Ряды. Примеры.
- •1. Числовые последовательности.
- •2.Сходимость числовых рядов.
- •3.Ряд Тейлора (Маклорена).
- •Де 9. Дифференциальные уравнения. Примеры
- •1. Типы уравнений.
- •2. Уравнения с разделяющимися переменными.
- •3.Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
- •Де 10. Теория вероятностей/ примеры
- •1.Определение вероятности.
- •2. Теоремы сложения и умножения вероятностей.
- •3. Числовые характеристики случайных величин
- •4. Законы распределения вероятностей дискретных случайных величин.
- •Де 11. Математическая статистика. Примеры
- •1. Характеристики вариационного ряда.
- •2.Точечные оценки параметров распределения.
- •3.Элементы корреляционного анализа.
- •4. Проверка статистических гипотез.
- •Де 12. Дискретная математика. Примеры
- •1. Операции над высказываниям.
- •2. Отношения между множествами.
- •1.Ориентированные графы.
- •Де 13. Численные методы примеры.
- •1.Интерполирование функций: интерполяционный многочлен Лагранжа.
- •2.Численные методы решения алгебраических уравнений (и систем).
- •3. Решения дифференциальных уравнений с помощью рядов.
Де 13. Численные методы примеры.
1.Интерполирование функций: интерполяционный многочлен Лагранжа.
1.
Интерполяционный многочлен Лагранжа,
составленный по таблице значений функции
![]()
 имеет
вид …
имеет
вид …![]()
2.
Функция
![]() представлена
таблицей:
представлена
таблицей:
 Тогда
в интерполяционном полиноме Лагранжа
2-ой степени с узлами
Тогда
в интерполяционном полиноме Лагранжа
2-ой степени с узлами
![]() ,
составленном по этой таблице для
приближенного вычисления
,
составленном по этой таблице для
приближенного вычисления
![]() при
условии
при
условии
![]() значение
значение
![]() не
может быть равно
…2,
3, 5 или 8.
не
может быть равно
…2,
3, 5 или 8.
3.
Интерполяционный многочлен Лагранжа
второй степени
![]() может
быть составлен по таблице значений
функции
может
быть составлен по таблице значений
функции
![]() вида
…
вида
…
4.
Функция
![]() представлена
таблицей
представлена
таблицей
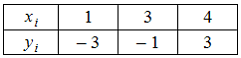 Тогда
значение
Тогда
значение
![]() ,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …(-3)
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …(-3)
5.
Функция
представлена
таблицей
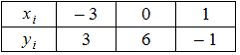 Тогда
значение
Тогда
значение
![]() ,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …(8).
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …(8).
6.
Интерполяционный
многочлен Лагранжа второй степени
![]() может
быть составлен по таблице значений
функции
может
быть составлен по таблице значений
функции
![]() вида
…
вида
…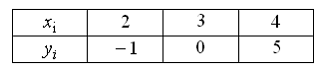
7.
Функция
представлена
таблицей:
 Тогда
график многочлена, интерполирующего
эту функцию, пересекает ось
в
точке с абсциссой …5,5.
Тогда
график многочлена, интерполирующего
эту функцию, пересекает ось
в
точке с абсциссой …5,5.
2.Численные методы решения алгебраических уравнений (и систем).
1.
Уравнение
![]() решается
методом касательных (Ньютона). Один из
корней принадлежит интервалу
решается
методом касательных (Ньютона). Один из
корней принадлежит интервалу![]() .
Тогда первое приближение
.
Тогда первое приближение
![]() к
точному корню
к
точному корню
![]() будет
вычисляться по формуле …
будет
вычисляться по формуле …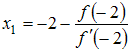
2.
Дана система из двух уравнений с двумя
неизвестными
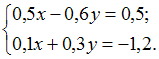 .
Начальное приближение имеет вид
.
Начальное приближение имеет вид
![]() .
Тогда для нахождения вектора погрешностей
.
Тогда для нахождения вектора погрешностей
![]() при
решении системы методом Ньютона получим
систему …
при
решении системы методом Ньютона получим
систему …
3.
Система линейных алгебраических
уравнений
 решается
методом простой итерации. Тогда для
этой системы необходимое условие
сходимости к точному решению …(
выполняется
только по столбцам)
решается
методом простой итерации. Тогда для
этой системы необходимое условие
сходимости к точному решению …(
выполняется
только по столбцам)
4.
Корень уравнения
![]() отделен
на отрезке [–1; 0].
отделен
на отрезке [–1; 0].
5.
Начальное приближение
![]() .
После выполнения одного шага метода
Ньютона (касательных) приближение
.
После выполнения одного шага метода
Ньютона (касательных) приближение
![]() ,
записанное с тремя знаками после запятой,
равно …(–
0,778)
,
записанное с тремя знаками после запятой,
равно …(–
0,778)
6.
Корень уравнения
![]() отделен
на отрезке …[–1;
0].
отделен
на отрезке …[–1;
0].
7.
Дано уравнение
![]() .
Один из корней этого уравнения принадлежит
интервалу …
.
.
Один из корней этого уравнения принадлежит
интервалу …
.
8.
Дано
уравнение
![]() .
Тогда один из корней этого уравнения
принадлежит интервалу …
.
Тогда один из корней этого уравнения
принадлежит интервалу …![]()
9.
Система
линейных алгебраических уравнений
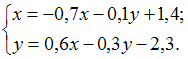 решается
методом простой итерации. Тогда первое
приближение к решению равно …
решается
методом простой итерации. Тогда первое
приближение к решению равно …![]()
3. Решения дифференциальных уравнений с помощью рядов.
1.
Три первых отличных от нуля члена
разложения в степенной ряд решения
дифференциального уравнения
![]() ,
удовлетворяющего начальным условиям
,
удовлетворяющего начальным условиям
![]() и
и
![]() ,
имеют вид …
,
имеют вид …![]()
2.
Первые
три отличных от нуля члена разложения
в степенной ряд решения задачи Коши
![]() имеют
вид …
имеют
вид …![]()
3.
Три первых отличных от нуля члена
разложения в степенной ряд решения
дифференциального уравнения
![]() ,
удовлетворяющего начальному условию
,
имеют вид …
,
удовлетворяющего начальному условию
,
имеют вид …![]()
4.
Второй
отличный от нуля член разложения в
степенной ряд решения дифференциального
уравнения
![]() ,
удовлетворяющего начальному условию
,
удовлетворяющего начальному условию
![]() ,
будет равен …
,
будет равен …![]()
