Распределение давления в установившемся изотермическом течении газа в газопроводе

Распределение давления по длине участка газопровода в упрщенном варианте получают из уравнений (13.7) и (13.13):

, (13.14)

а также уравнения состояния газа.

Преобразование второго уравнения системы (13.14) дает:

.

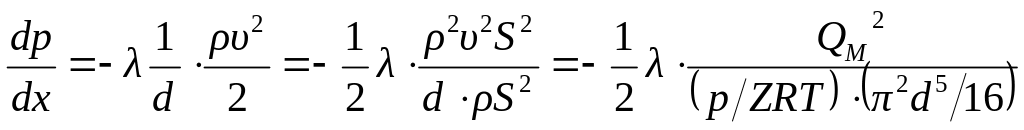Если принять упрощающие допущения:

• 

• ;

• ,

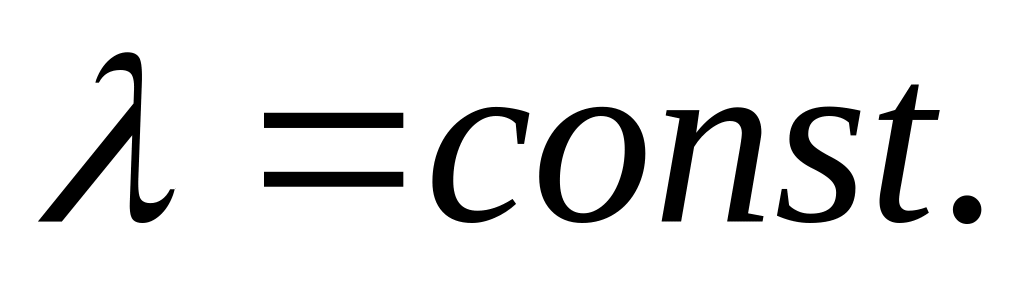
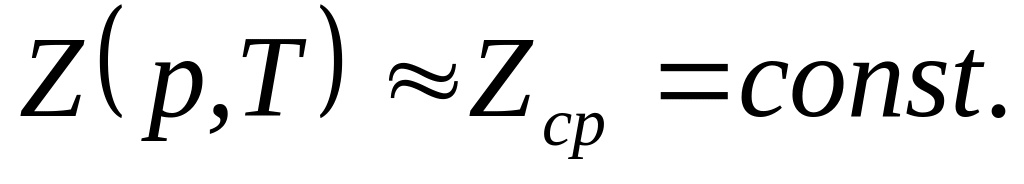то полученное дифференциальное уравнение интегрируется и дает формулу для распределения давления по длине участка газопровода. Имеем:

или

. (13.15)

Здесь использовано начальное условие, согласно которому .

Формула (13.15) означает, что квадрат давления газа линейно уменьшается по длине участка газопровода:

, (13.16)

где давление газа в конце участка.

Если определить среднее давление газа на участке газопровода выражением

,

то, подставив в него распределение из (13.16), найдем:

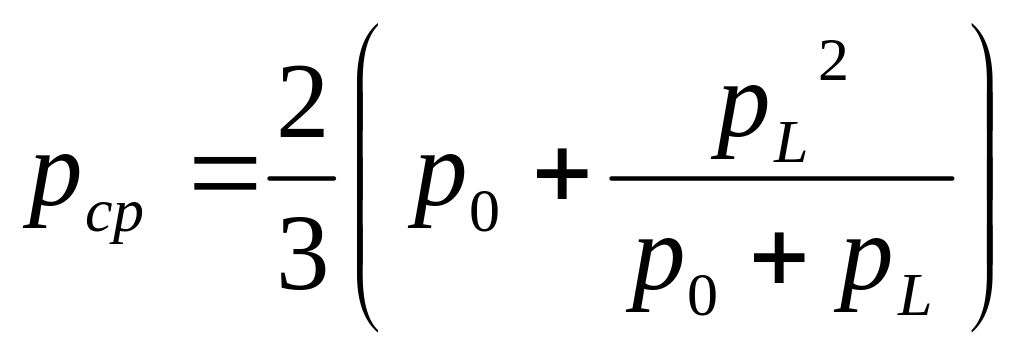. (13.17)

Из (13.15) находятся, в частности:

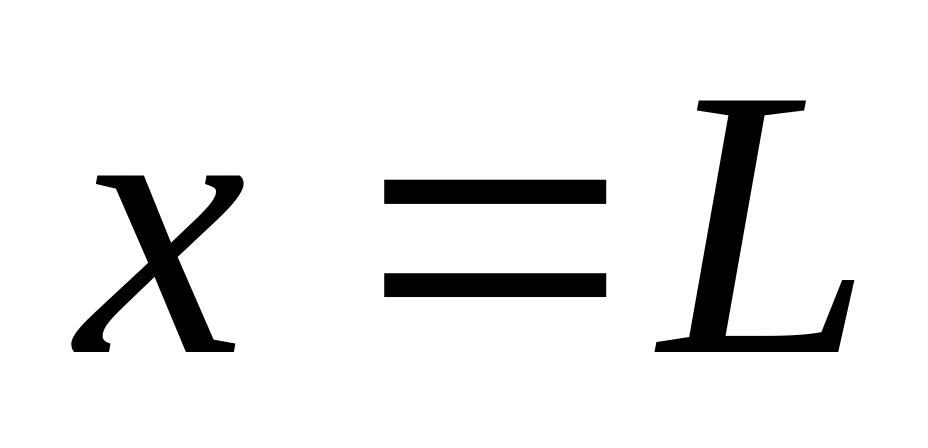• давление (в Па в системе СИ) в конце участка газопровода по известному массовому расходу :

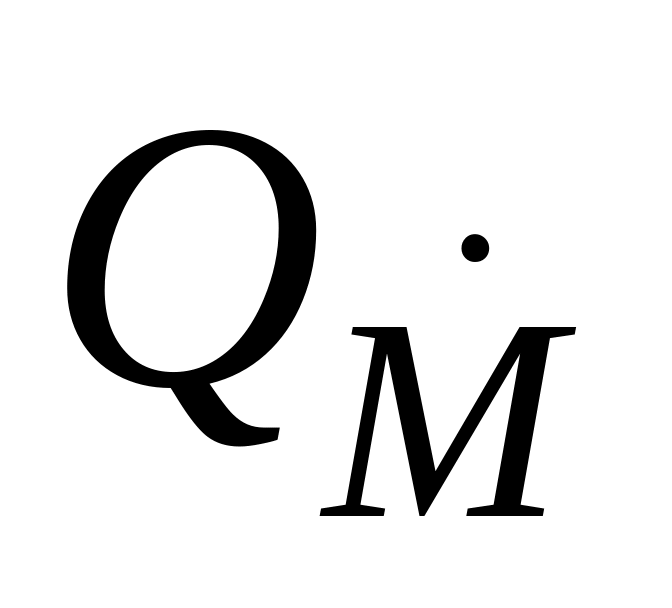или

; (13. 18)

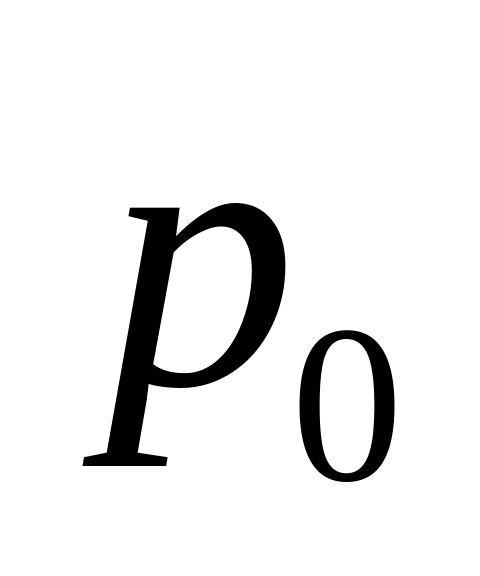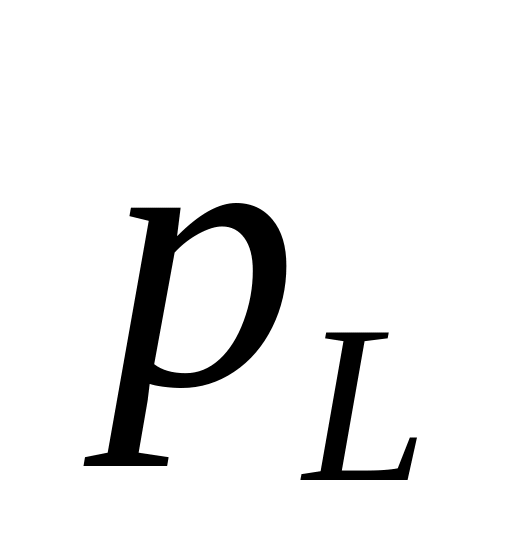• массовый расход (в кг/с в системе СИ) по известным давлениям и в начале и в конце участка газопровода:

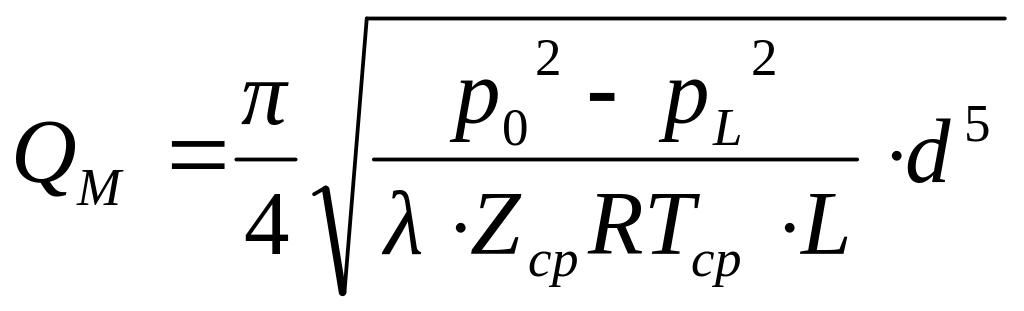. (13.19)

Если, в частности, принять для формулу (13.10), то массовый расход газа оказывается прямо пропорциональным - корню квадратному из разности квадратов давлений в начале и в конце участка газопровода, - диаметру газопровода в степени 2,6 и обратно пропорциональным корню квадратному из протяженности участка, т.е.

 .

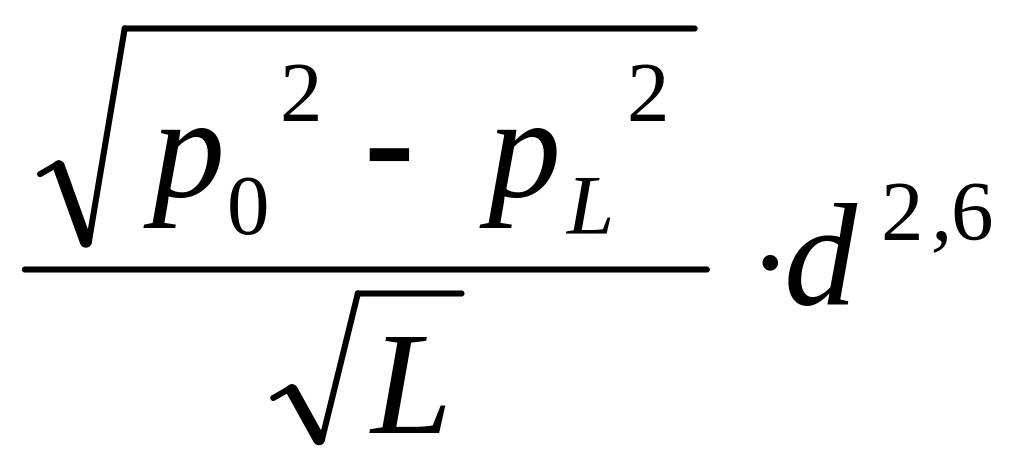Пример. Найти коммерческий расход газа ( кг/м³) на участке газопровода ( мм, км, мм), если давление в начале участка составляет 5,5 МПа, а в его конце – 3,8 МПа. Принять, что температура газа постоянна вдоль всего участка и равна +10°С, а среднее значение коэффициента сверхсжимаемости равно 0,9.

Решение. Коммерческий расход газа - это массовый расход газа, выраженный в объемных единицах - стандартных кубических метрах, т.е. , где плотность газа при стандартных условиях ( Па, К), поэтому

.

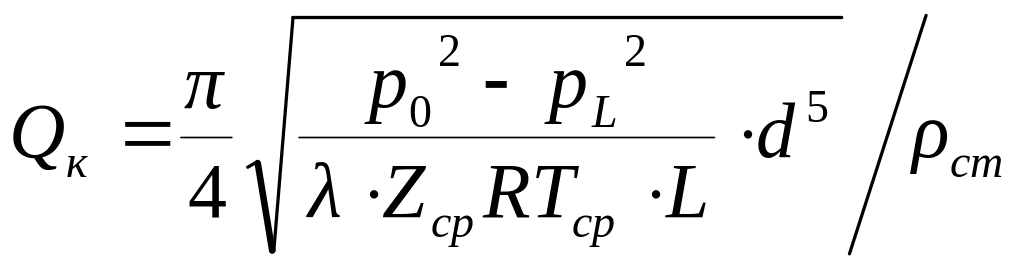Поскольку , то

Дж/(кг К).

Коэффициент гидравлического сопротивления рассчитывается по формуле (13.10):

.

Далее вычисляется коммерческий расход газа:

м³/c

=48,77 млн. м³/сут.

Ответ. или млн. м³/сут.

Уравнение энергии

Уравнение изменения полной энергии газа, выражающее первый закон термодинамики, в общем случае имеет вид:

,

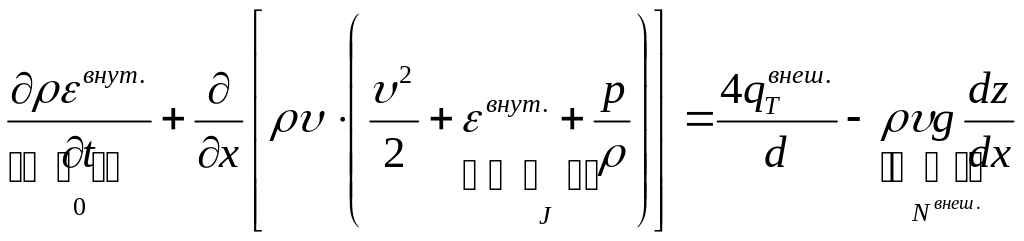где внутренняя энергия единицы массы газа; энтальпия единицы массы газа; внешний теплоприток (количество тепла, передаваемое газу извне в единицу времени через единицу поверхности трубопровода, . Левая часть уравнения энергии дает изменение в единицу времени полной энергии газа, причем первое слагаемое в правой части – это секундный приток внешнего тепла; второе – работа в единицу времени (т.е. мощность) внешних сил (в данном случае силы тяжести).

Для установившегося течения , поэтому уравнение энергии упрощается:

. (13.20)

Если в последнем уравнении использовать зависимость энтальпии от давления и температуры , положив , а также принять для , выражение

, (13.21)

называемое законом теплообмена Ньютона (здесь температуры внутри и вне трубопровода; коэффициент теплопередачи), то уравнение (13.20) можно преобразовать следующим образом:

.

Обозначая и , получаем:

или

. (13.22)

Здесь теплоемкость газа при постоянном давлении; коэффициент Джоуля-Томпсона.

Используя выражение энтальпии газа через внутреннюю энергию и другие параметры состояния

,

можно выразить эти коэффициенты через коэффициенты и :

;

.

Поскольку при движении газа в газопроводе , а , если (см. диаграммы на рис. 13.2), то эффект Джоуля-Томпсона состоит в дополнительном охлаждение газа за счет падения давления. Очевидно, что этот эффект проявляется только для реального газа, для которого . Как правило, значения коэффициента составляют К/МПа.

Упрощенное уравнение. Если в уравнении (13.22) пренебречь эффектом Джоуля-Томпсона, а также пренебречь измененим кинетической энергии и работой силы тяжести, то уравнение изменения энергии упрощается и приобретает вид:

. (13.23)