13.2. Уравнения установившегося течения газа в трубопроводе

Для описания установившегося стационарного течения газа в трубопроводе используются основные законы механики: уравнение сохранения массы газа (уравнение неразрывности потока), уравнение изменения количества движения (уравнение движения) и уравнение изменения полной энергии газа (уравнение энергии).

Уравнение неразрывности потока газа в трубе

Уравнение неразрывности потока газа, выражающее закон сохранения массы газа, движущегося в трубе, имеет вид:

(13.6)

Поскольку течение считается установившимся, то , поэтому уравнение упрощается:

.

Отсюда следует, что массовый расход газа остается постоянным для всех сечений газопровода:

(13.7)

Поскольку плотность газа уменьшается по мере продвижения газа вследствие уменьшения давления, то из (13.6) следует, в частности, что в газопроводе с постоянным диаметром ( ) скорость газа увеличивается от начала участка газопровода к его концу.

Уравнение движения

Уравнение движения газа, выражающее закон изменения количества движения под действием внешних сил (второй закон Ньютона) записывается в следующем виде:

.

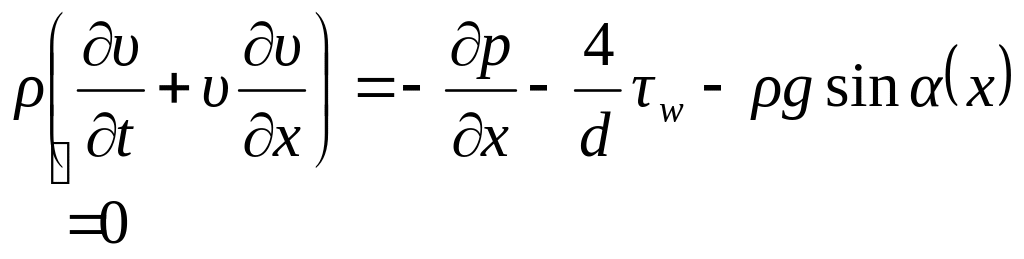Поскольку течение газа установившееся, то это уравнение упрощается:

. (13.8)

Для величины касательного напряжения сил трения газа о внутреннюю поверхность трубопровода обычно используют формулу:

, (13.9)

где коэффициент трения или коэффициент гидравлического сопротивления ( ).

В общем случае коэффициент гидравлического сопротивления при течении газа по трубопроводу зависит как от числа Рейнольдса , так и от эквивалентной шероховатости внутренней поверхности трубопровода. Однако для магистральных газопроводов числа Рейнольдса составляют миллионы, в силу чего коэффициент зависит только от состояния внутренней поверхности трубопровода. Для расчета в магистральных газопроводах рекомендуется формула ВНИИГаза:

. (13.10)

В рамках принятых допущений уравнение установившегося течения газа в трубопроводе приобретает вид:

. (13.11)

Отметим, что где зависимость геометрической высоты сечения газопровода над уровнем моря от координаты , отсчитываемой вдоль оси трубопровода.

Упрощающее допущение. Поскольку скорость газа увеличивается, то ускорение частиц газа отлично от нуля, однако в длинных газопроводах это ускорение чрезвычайно мало и потому им можно пренебречь. Справедлива следующая оценка:

.

Эта оценка справедлива, если скорость газа в трубопроводе (составляющая, как правило, м/c) много меньше скорости звука (равная примерно 380-440 м/c), т.е. . Например, для газа с плотностью кг/м³, движущегося в газопроводе со скоростью , изменение слагаемого при изменении скорости на 5 м/c составляет: Па, в то время как изменение слагаемого в правой части уравнения в 18 раз больше: . Вот почему, в уравнении движения, как правило, пренебрегают инерцией, т.е. не учитывают ускорение газа.

С учетом данной оценки уравнение движения газа в газопроводе выражает обычно равенство движущей силы давления и препятствующих ему силы трения и силы тяжести:

. (13.12)

Поскольку природный газ – это относительно легкая среда, то во многих случаях пренебрегают также силой тяжести , поэтому уравнение (13.12) движения газа еще более упрощается:

. (13.13)