Глава 13

Глава 13 стационарное течение газа в трубопроводе

Природным газом обычно называют тот углеводородный газ, который добывают из многочисленных газовых месторождений в мире. Природный газ представляет собой смесь различных газов, причем не только углеводородных, однако, метан ( ) составляет в каждой такой смеси основную часть, как правило, более 90%. Углеводородными составляющими природного газа являются метан, этан, пропан, бутан и т.д., а неуглеводородными – азот, кислород, сероводород, углекислый газ, водород, гелий и др. Природный газ каждого месторождения имеет индивидуальный состав, отличающий его от газа других месторождений.

Плотность природного газа при атмосферном давлении и температуре составляет , иными словами, природный газ легче воздуха. Природный газ не имеет цвета и запаха, а тот известный неприятный запах – это запах этилмеркаптана, специального одоранта, который добавляется в газ на газораспределительных станциях, для того чтобы можно было чувствовать наличие газа в помещении.

13.1. Физические свойства природного газа

Одно из основных свойств природного газа, отличающее его от капельных жидкостей, является свойство сжимаемости. Сжимаемость газа, т.е. изменение его объема при увеличении давления, значительно выше, чем у капельных жидкостей. Так, например, если давление в газе, находящемся при атмосферном давлении, увеличить в 50 раз, то его объем уменьшится примерно во столько же раз, в то время как объем жидкости практически не изменится.

Для всех газов в состоянии термодинамического равновесия существует соотношение между давлением p, абсолютной температурой и плотностью (или удельным объемом ):

, (13.1)

называемое уравнением состояния. Физическая природа этого обстоятельства обсуждается в курсах статистической физики. В большинстве моделей, описывающих свойства газа, используется также предположение о том, что при возникновении движения соотношение (13.1) сохраняется. Фактически, это допущение эквивалентно предположению, что процессы установления термодинамического равновесия происходят намного быстрей, чем неравновесность, которую вносит в систему возникающее движение.

Конкретный вид зависимости (13.1) устанавливается в ходе так называемых калориметрических измерений, однако для большинства газов эта зависимость имеет одни и те же характерные особенности. Геометрически зависимость (13.1) представляется двумерной поверхностью в трехмерном пространстве переменных ( ). На рис. 13.1 представлены изотермы реальных газов, т.е. сечение этой поверхности плоскостями

Для всех газов существует так называемая критическая изотерма (на рис.13.1 выделена жирной линией), выше и ниже которой свойства газа качественно различны. Если , где критическая температура данного газа, то газ при любом повышении давления остается в газообразном состоянии; если же , то для каждой температуры существует такое значение давления , при котором газ начинает переходить в жидкую фазу, причем его удельный объем уменьшается от значения до значения , после чего получившаяся среда проявляет уже свойства жидкости.

p

p_кр К

Модель

совершенного газа

Рис. 13.1. Изотермы газов.

Точка К называется критической точкой данного газа при этом величины ( ) отражают индивидуальные свойства газа и являются его константами. Например, для метана СН₄, из которого в основном состоит природный газ, 190,55 К и 4,641 МПа. Это означает, что если температура газа выше 190,55 К, то газ ни при каком повышении давления не может быть переведен в жидкое состояние.

Совершенный газ. Если, однако, давление в газе не слишком высокое, а температура - не слишком низкая, то изотермы всех газов подобны друг другу (см. правую часть рис. 13.1, заключенную в пунктирном овале) и с большой степенью точности приближаются гиперболами: давление р обратно пропорционально удельному объему .

При указанных условиях взаимодействие молекул реального газа не зависит от формы молекул (т.е. от пространственной конфигурации входящих в них атомов), а определяется лишь общей массой. Образно говоря, молекулы ведут себя подобно шарам, отличающимся друг от друга только массой, поэтому число параметров, характеризующих газ, уменьшается с трех до одного: молярной массы.

Для характеристики термодинамического состояния газов в указанной области давлений и температур используется модель совершенного газа. Уравнение (13.1) состояния газа в этом случае имеет наиболее простой вид:

или , (7.2)

где единственная входящая в уравнение константа называется газовой постоянной, причем , универсальная газовая постоянная, равная 8314 Дж/(моль К). Таким образом, для совершенных газов все газовые постоянные зависят только от молярной массы. Например, для метана ( кг/кмоль): Дж/(кг К); для О₂ - кислорода ( кг/кмоль): Дж/(кг К); для СО₂ - углекислого газа ( кг/кмоль): Дж/(кг К); для воздуха ( кг/кмоль): Дж/(кг К) и т.д.

Уравнение (13.2), связывающее между собой плотность давление и температуру газа, называется уравнением Клапейрона - Менделеева. Модель совершенного газа достаточно эффективно работает в интервале не слишком высоких давлений и умеренных температур. В противном случае используется модель так называемого реального газа.

Реальный газ. Из рис. 13.1 следует, что гиперболическая зависимость (13.2) не соответствует наблюдениям при увеличении давления или сильном уменьшении температуры. Поэтому в процессах, происходящих с газом, в том числе и при его транспортировке по трубопроводам или хранении в подземных газохранилищах, где давление составляет МПа, модель совершенного газа, будь она использована в расчетах, давала бы неправильные результаты.

Существует модель, более общая, чем модель совершенного газа - модель реального газа. В математической записи она представляется соотношением:

или , (13.3)

отличающимся от (13.2) тем, что в него входит безразмерный коэффициент называемый коэффициентом сверхсжимаемости, являющийся функцией двух параметров - приведенного давления и приведенной температуры :

, ,

здесь и критические давление и температура газа, о которых говорилось выше.

Таким образом, модель (13.3) учитывает не только молекулярный вес газа (через константу ), но и такие термодинамические постоянные, как его критические давление и температуру. Очевидно также, что для умеренных давлений и температур и модель (13.3) естественным образом трансформируется в модель (13.2) совершенного газа. Для реального газа . Графики функции представлены на рис. 13.2.

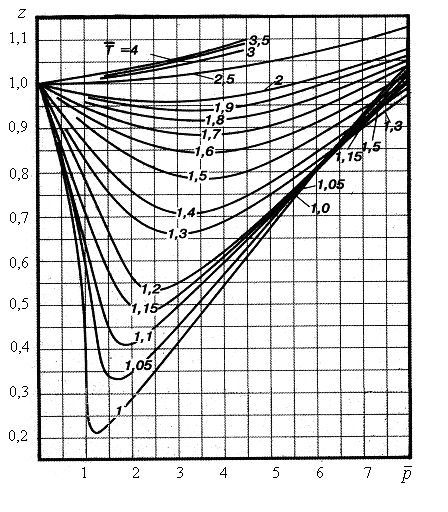
Рис. 13.2. Графики для природного газа

Пример. Найти значение коэффициента сверхсжимаемости газа ( 4,6 МПа, 190 К), находящегося при давлении 7,5 МПа и температуре 288 К.

Решение. Сначала вычисляем приведенные параметры состояния: ; . По графикам на рис. 13.2 находим: .

Существует множество аппроксимационных формул для вычисления коэффициента . Фактически речь идет об аппроксимации уравнения состояния (13.1). Однако свойства реальных газов столь сложны, что универсальных формул для всех газов и во всем диапазоне изменения определяющих параметров не существует, поэтому в разных случаях используются различные приближенные формулы. Например, для газа, текущего в газопроводе, т.е. газа, находящегося в термодинамических условиях К и МПа, рекомендуется использовать формулу

, (13.4)

Пример. Найти значение коэффициента сверхсжимаемости газа ( 4,6 МПа, 190 К), находящегося при давлении 7,5 МПа и температуре 288 К (см. предыдущий пример).

Решение. Сначала рассчитываем значения приведенных давления и температуры:

, ;

затем находим параметр :

,

и, наконец, вычисляем коэффициент :

.

Отсюда следует, что погрешность расчетов по формулам (13.4) не превышает 0,8%.

Молярная масса (кг/кмоль) и критические параметры (МПа) и (К) газовой смеси допускается вычислять по следующим аддитивным формулам:

; ; , (13.5)

где объемные доли компонентов, составляющих газ; соответствующие постоянные этих компонентов.

Некоторые постоянные компонентов, составляющих природный газ, приведены в таблице 13.1.

Плотность природного газа при так называемых стандартных условиях, т.е. при давлении 101325 Па (760 мм. рт.ст.) и температуре 20⁰С (293 К), составляет примерно 0,72 кг/м³, что меньшее плотности воздуха кг/м³ при тех же условиях, последнее означает, что природный газ легче воздуха.

Таблица 13.1.

Некоторые физические постоянные газов

Газ	Молярная масса, кг/кмоль	Критическое давление, МПа	Критическая температура, К
Метан	16,042	4,641	190,55
Этан	30,068	4,913	305,50
Пропан	44,094	4,264	369,80
Изобутан	58,120	3,570	407,90
Н – Бутан	58,120	3,796	425,17
Н – Пентан	72,146	3,374	469,78
Азот	28,016	3,396	126,25
Кислород	32,000	4,876	154,18
Сероводород	34,900	8,721	373,56
Углекислый газ	44,011	7,382	304,19
Водород	2,020	1,256	33,10
Гелий	4,000	0,222	5,00
Воздух	28,966	3,780	132,46

Пример. Характеристики газовой смеси представлены в таблице 13.2.

Таблица 13.2.

Компонента газа	Объемная доля, %	Критическое давление, МПа	Критическая температура, К
Метан	92,0	4,641	190,55
Этан	4,0	4,913	305,50
Азот	2,0	3,396	126,25
Сероводород	1,0	8,721	373,56
Углекислый газ	1,0	7,382	304,19

Найти значения коэффициента Z сжимаемости и плотности этой смеси при давлении 6,5 МПа и температуре +25°С.

Решение. Молярная масса смеси, критического давления и критической температуры смеси рассчитываются по формулам (13.5):

кг/моль,

МПа,

Дж/(кг К);

Затем определяются приведенные параметры и газовой смеси:

, .

По формулам (13.4) вычисляеися :

Вычисляются коэффициент

и плотность сжатого газа:

кг/м³.

Ответ. ; кг/м³.