5.8. Метод интеграла Дюамеля

Он позволяет находить отклик цепи при нулевых начальных условиях при произвольном входном сигнале и известной переходной (или импульсной) характеристике цепи h(t) (рис. 5.23).

Произвольный импульсный сигнал (рис. 5.24) заменим совокупностью элементарных ступенчатых сигналов с амплитудами ∆х, возникающими в моменты времени τ_к со сдвигом по времени на .

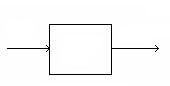
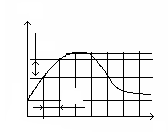
Рис.5.23 Рис. 5.24

Как следует из рис.5.24, х₀ – амплитуда нулевого ступенчатого сигнала. Тогда отклик на него ; – амплитуда элементарного ступенчатого сигнала, рассчитывается из выражения , где х' (τ_к) – производная от сигнала в момент времени τ_к, она равна тангенсу угла наклона сигнала в момент времени τ_к. Тогда отклик на элементарный ступенчатый сигнал .

Используя принцип суперпозиции и переходя к пределу суммы при Δτ→0 (Δτ = dτ), можно записать

.

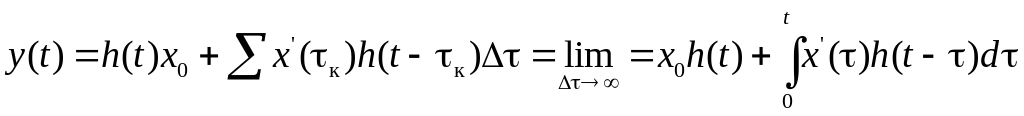Последнее выражение и называется интегралом Дюамеля. Оно позволяет получить отклик на заданное воздействие в любой момент времени t после коммутации. Интегрирование ведется по τ – текущее время (0 < τ < t), причем выражения х'(τ) и h(t – τ) получают из выражений для х(t) и h(t) путем замены t на τ и t – τ.

5.8. Связь между дифференциальным уравнением и характеристиками электрической цепи

1) Для линейной цепи при произвольном входном сигнале х(t) связь между выходным и входным сигналом записывается в виде дифференциального уравнения

.

2) Связь дифференциального уравнения с частотной передаточной функцией.

П о определению, частотная функция есть H(jω)= .

Если входной сигнал гармонический

,

если цепь линейная, то выходной сигнал обязательно гармонический:

.

Подставим (6.1) и (6.2) в дифференциальное уравнение

В результате получим

.

3) Связь частотной с операторной функцией цепи Н(р).

По определению, Н(р) = H(jω)|_jω→p. Отсюда

.

4) Связь между импульсной и переходной характеристикой g(t) и h(t). Так как , то .

5) Связь между g(t) и H(jω), H(p).

Из спектрального анализа следует выходной сигнал

.

Если , то спектр . Следовательно, импульсная характеристика – это обратное преобразование Фурье (ОПФ) частотной функции цепи, а частотная функция – прямое преобразование Фурье (ППФ) импульсной характеристики.

Таким образом, все способы описания электрической цепи связаны между собой.

Контрольные вопросы

1. с чем связано возникновение переходных процессов в электрической цепи?

2. В чем заключается классический и спектральный методы анализа линейных цепей?

3. В чем заключается суть анализа линейных цепей методом интеграла Дюамеля?

4. Каков характер переходной характеристики в цепи первого порядка?

5. Как формулируются законы коммутации?

6. Какими основными свойствами обладает единичная функция?

7. Как дифференцирующая и интегрирующая цепи влияют на импульсные сигналы?

8. На вход цепи с операторной передаточной функцией вида K_u(p) = (1+pτ)^–1 воздействует гармонический сигнал s₁(t)=A cos(ωt). Записать отклик.

9. В каких задачах удобен спектральный метод анализа?

10. Для каких целей применяется интегрирующая цепь?

11. Как связаны между собой импульсная и переходная характеристика линейной цепи?

19