5.5. Расчет переходных характеристик последовательного колебательного контура
Схема последовательного колебательного контура приведена на рис. 5.15 а.
Для расчета переходной характеристики установим связь между выходным u2 и входным u1 напряжениями. Входной сигнал имеет вид ступенчатого напряжения , тогда переходная характеристика h(t) находится из выражения h(t) = u2(t)/E, где u2(t) – выходное напряжение.
C
C
R
R
а
б
u2()
= E
u2(0)
= 0
u2(t)
E
u1(t)
L
C
R
L
E
L
i(0)
= 0
в |
|
Рис. 5.15 |
|
Задачу будем решать классическим способом. За переменную в составляемом уравнении выбираем переменную, характеризующую энергетическое состояние цепи и наиболее просто связанную с выходным сигналом. Такой переменной является напряжение на конденсаторе uС(t) = u2(t).
1) Составим дифференциальное уравнение относительно переменной состояния цепи и приведем его к стандартному виду.
Данная цепь представляет контур, а потому, используя второй закон Кирхгофа и соотношения между напряжениями и токами на элементах схемы, запишем:
;
,
.
Отсюда
;
.
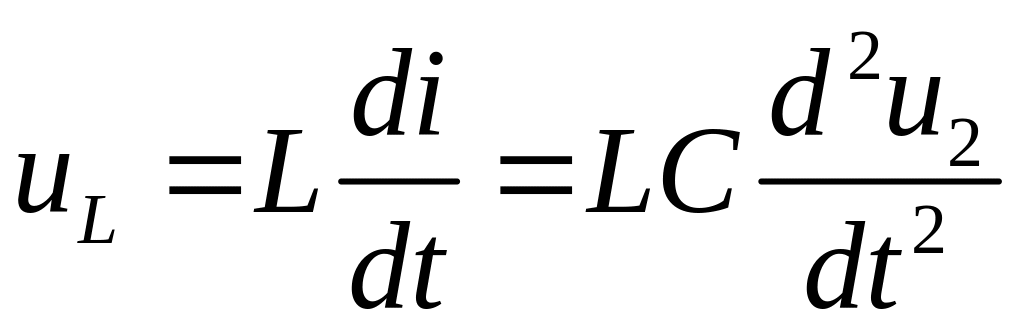Подставим полученные напряжения в первое выражение:
.
Поделим на LC
и введем обозначения
.
Получим
2) Запишем общее решение:
3) Найдем вынужденную
составляющую общего решения
.
Для этого составим
схему замещения исходной цепи при t
∞, соответствующую
(рис. 5.15 б), из которой и получим
=E
4) Найдем коэффициенты показателей экспоненты р1 и p2, которые являются корнями характеристического уравнения:
.
Отсюда
.
5) Найдем постоянные интегрирования А1, А2 из начальных условий, т.е. при t = +0 для искомой функции, и ее производной согласно схеме в момент после коммутации (при t = +0, ω ∞), которая приведена на рис. 5.15 в.
Составим систему:
;
,
или,
в матричной форме:
,
– из решения которой и находим А1
и А2:
.
6) Анализ корней и запись окончательного решения:
а) если
,
то корни
–
отрицательные действительные числа.
Тогда
,
И окончательное решение записывается так:
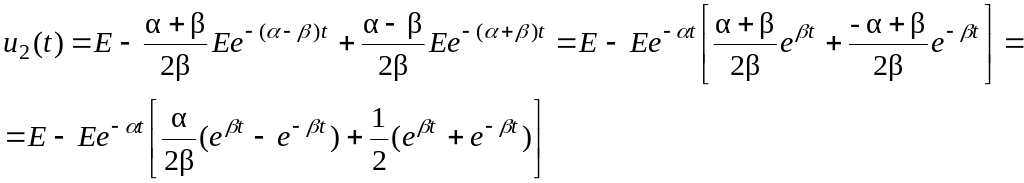Учитывая,
что
;
,
а также, что при βt
0,
,
окончательно получим:
.
Такое решение называется апериодическим (рис. 5.16).
E
u2
> 0
t |
Рис. 5.16 |
,
то корни
комплексно сопряженные числа. В полученном
решении нужно вместо
подставить мнимое число j.
Тогда, если учесть, что
;
,
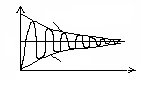
то при α << β, получим следующее (рис. 5.17):
E
t
= 02–2
e–t |
Рис. 5.17 |
.
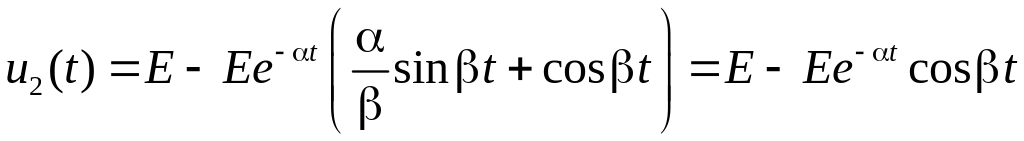Здесь ω0 = (LC)–1 – собственная частота колебательного контура; β = (ω02 – α2)1/2 – частота собственных колебаний в контуре при наличии резистивных потерь; α = R/(2L) – скорость затухания собственных колебаний в контуре, α =1/τ, где τ = 2L/R – постоянная времени контура.