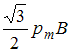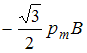- •Задание n 15 Тема: Средняя энергия молекул
- •Задание n 16 Тема: Распределения Максвелла и Больцмана
- •Задание n 24 Тема: Электростатическое поле в вакууме
- •Задание n 1 Тема: Работа. Энергия
- •Задание n 8 Тема: Поляризация и дисперсия света
- •Задание n 14 Тема: Средняя энергия молекул
- •Задание n 26 Тема: Электрические и магнитные свойства вещества
- •Задание n 3 Тема: Электрические и магнитные свойства вещества
- •Задание n 7 Тема: Спектр атома водорода. Правило отбора
- •Задание n 8 Тема: Уравнение Шредингера (конкретные ситуации)
- •Задание n 9 Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Задание n 12 Тема: Средняя энергия молекул
- •Задание n 24 Тема: Динамика поступательного движения
- •Задание n 25 Тема: Кинематика поступательного и вращательного движения
- •Задание n 26 Тема: Элементы специальной теории относительности
- •Задание n 1 Тема: Элементы специальной теории относительности
- •Задание n 2 Тема: Динамика вращательного движения
- •Задание n 9 Тема: Электрические и магнитные свойства вещества
- •Задание n 10 Тема: Уравнения Максвелла
- •Задание n 11 Тема: Явление электромагнитной индукции
- •Задание n 17 Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Задание n 18 Тема: Уравнение Шредингера (конкретные ситуации)
- •Задание n 19 Тема: Уравнения Шредингера (общие свойства)
- •Задание n 22 Тема: Первое начало термодинамики. Работа при изопроцессах
- •Задание n 23 Тема: Средняя энергия молекул
- •Задание n 4 Тема: Элементы специальной теории относительности
- •Задание n 5 Тема: Законы сохранения в механике
- •Задание n 8 Тема: Динамика вращательного движения
- •Задание n 9 Тема: Работа. Энергия
- •Задание n 10 Тема: Уравнения Шредингера (общие свойства)
- •Задание n 11 Тема: Спектр атома водорода. Правило отбора
- •Задание n 12 Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Задание n 13 Тема: Уравнение Шредингера (конкретные ситуации)
- •Задание n 14 Тема: Явление электромагнитной индукции
- •Задание n 15 Тема: Электрические и магнитные свойства вещества
- •Задание n 16 Тема: Магнитостатика
- •Задание n 23 Тема: Второе начало термодинамики. Энтропия
- •Задание n 24 Тема: Средняя энергия молекул
- •Задание n 5 Тема: Уравнения Максвелла
- •Задание n 6 Тема: Явление электромагнитной индукции
- •Задание n 7 Тема: Спектр атома водорода. Правило отбора
- •Задание n 8 Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
- •Задание n 11 Тема: Распределения Максвелла и Больцмана
- •Задание n 14 Тема: Второе начало термодинамики. Энтропия
- •Задание n 18 Тема: Законы сохранения в механике
- •Задание n 21 Тема: Энергия волны. Перенос энергии волной
- •Задание n 24 Тема: Тепловое излучение. Фотоэффект
- •Задание n 25 Тема: Интерференция и дифракция света
- •Задание n 26 Тема: Поляризация и дисперсия света
Задание n 24 Тема: Электростатическое поле в вакууме
Электростатическое
поле создано системой точечных зарядов
![]() и
и
![]() (см.
рис.).
(см.
рис.).
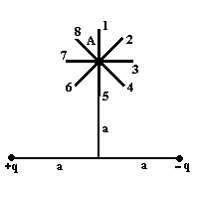 Градиент
потенциала поля в точке А ориентирован
в направлении …
Градиент
потенциала поля в точке А ориентирован
в направлении …
|
|
|
7 |
|
|
|
3 |
|
|
|
1 |
|
|
|
5 |
Решение:
Градиент
потенциала в некоторой точке связан с
напряженностью поля в этой точке
соотношением
![]() ,
поэтому для нахождения
,
поэтому для нахождения
![]() в
точке А необходимо найти напряженность
поля в этой точке. Согласно принципу
суперпозиции полей, напряженность в
точке А равна:
в
точке А необходимо найти напряженность
поля в этой точке. Согласно принципу
суперпозиции полей, напряженность в
точке А равна:
![]() ,
где
,
где
![]() и
и
![]() –
напряженности полей, создаваемых
точечными зарядами
и
в
рассматриваемой точке соответственно.
Вектор
ориентирован
в направлении 2, вектор
–
в направлении 4.
Величина напряженности
поля точечного заряда определяется по
формуле
–
напряженности полей, создаваемых
точечными зарядами
и
в
рассматриваемой точке соответственно.
Вектор
ориентирован
в направлении 2, вектор
–
в направлении 4.
Величина напряженности
поля точечного заряда определяется по
формуле
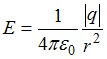 ,
где
,
где
![]() электрическая
постоянная, а r
– расстояние
от заряда до точки. Поскольку заряды
одинаковы по величине и удалены от точки
А на одинаковом расстоянии, то
электрическая
постоянная, а r
– расстояние
от заряда до точки. Поскольку заряды
одинаковы по величине и удалены от точки
А на одинаковом расстоянии, то
![]() .
Вектор
.
Вектор
![]() по
величине равен диагонали квадрата,
построенного на векторах
и
как
на сторонах, и ориентирован в направлении
3. Тогда вектор
ориентирован
в направлении 7.
по
величине равен диагонали квадрата,
построенного на векторах
и
как
на сторонах, и ориентирован в направлении
3. Тогда вектор
ориентирован
в направлении 7.
ЗАДАНИЕ N 25 Тема: Законы постоянного тока
На
рисунке показана зависимость силы тока
в электрической цепи от времени.
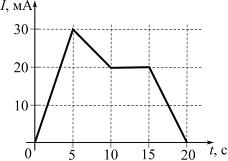 Заряд
(в мКл),
протекающий через поперечное сечение
проводника в промежутке времени
Заряд
(в мКл),
протекающий через поперечное сечение
проводника в промежутке времени
![]() ,
равен …
,
равен …
|
|
|
75 |
|
|
|
100 |
|
|
|
125 |
|
|
|
50 |
ЗАДАНИЕ N 26 Тема: Магнитостатика
Виток с магнитным
моментом
![]() свободно
установился в однородном магнитном
поле с индукцией
свободно
установился в однородном магнитном
поле с индукцией
![]() .
Если виток повернуть на угол 30о
вокруг оси, лежащей в плоскости витка,
то на него будет действовать вращающий
момент, равный
.
Если виток повернуть на угол 30о
вокруг оси, лежащей в плоскости витка,
то на него будет действовать вращающий
момент, равный
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
На
контур с током (виток) в однородном
магнитном поле действует вращающий
момент
![]() ,
стремящийся расположить контур таким
образом, чтобы вектор его магнитного
момента
был
сонаправлен с вектором магнитной
индукции
поля.
Модуль вращающего момента
,
стремящийся расположить контур таким
образом, чтобы вектор его магнитного
момента
был
сонаправлен с вектором магнитной
индукции
поля.
Модуль вращающего момента
![]() ,
где
,
где
![]() –
угол между направлением магнитного
поля и вектором
магнитного
момента витка. В исходном состоянии
–
угол между направлением магнитного
поля и вектором
магнитного
момента витка. В исходном состоянии
![]() ,
после поворота на
угол 30о
вокруг оси, лежащей в плоскости витка,
,
после поворота на
угол 30о
вокруг оси, лежащей в плоскости витка,
![]() .
Тогда
.
Тогда
![]() .
.
Задание n 1 Тема: Работа. Энергия
Потенциальная
энергия частицы задается функцией
![]() .
.
![]() –
компонента (в Н)
вектора силы, действующей на частицу в
точке А (1, 2, 3), равна …
(Функция
и
координаты точки А и заданы в единицах
СИ.)
–
компонента (в Н)
вектора силы, действующей на частицу в
точке А (1, 2, 3), равна …
(Функция
и
координаты точки А и заданы в единицах
СИ.)
|
|
|
– 4 |
|
|
|
4 |
|
|
|
12 |
|
|
|
– 12 |
Решение:
Связь
между потенциальной энергией частицы
и соответствующей ей потенциальной
силой имеет вид
![]() ,
или
,
или
![]() ,
,
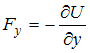 ,
,
![]() .
Таким образом,
.
Таким образом,
![]()
ЗАДАНИЕ N 2 Тема: Динамика вращательного движения
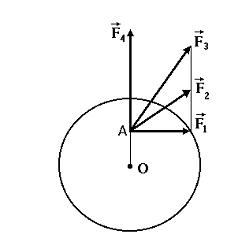
Диск может вращаться
вокруг оси, перпендикулярной плоскости
диска и проходящей через его центр. В
точке А прикладывают одну из сил (
,
,
или
),
лежащих в плоскости диска. Не
создает
вращающего момента относительно
рассматриваемой оси сила …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 3 Тема: Динамика поступательного движения
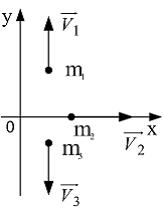
Система состоит
из трех материальных точек массами
![]()
![]() и
и
![]() которые
движутся так, как показано на рисунке.
которые
движутся так, как показано на рисунке.
 Если
скорости шаров равны
Если
скорости шаров равны
![]()
![]()
![]() то
вектор скорости центра
масс этой
системы ориентирован …
то
вектор скорости центра
масс этой
системы ориентирован …
|
|
|
в положительном направлении оси OX |
|
|
|
в отрицательном направлении оси OX |
|
|
|
в положительном направлении оси OY |
|
|
|
в отрицательном направлении оси OY |
ЗАДАНИЕ N 4 Тема: Кинематика поступательного и вращательного движения
На рисунке представлены графики зависимости скорости четырех тел, движущихся прямолинейно, от времени. Наибольшее перемещение за совершено телом …
|
|
|
3 |
|
|
|
1 |
|
|
|
2 |
|
|
|
4 |
ЗАДАНИЕ N 5 Тема: Законы сохранения в механике
Фигурист вращается вокруг вертикальной оси с определенной частотой. Если он разведет руки в стороны, увеличив тем самым свой момент инерции относительно оси вращения в 1,5 раза, то …
|
|
|
частота вращения фигуриста и его кинетическая энергия вращения уменьшатся в 1,5 раза |
|
|
|
частота вращения фигуриста возрастет в 1,5 раза, а его кинетическая энергия вращения – в 2,25 раза |
|
|
|
частота вращения фигуриста уменьшится в 1,5 раза, а его кинетическая энергия вращения – в 2,25 раза |
|
|
|
частота вращения фигуриста и его кинетическая энергия вращения возрастут в 1,5 раза |
Решение:
Согласно
закону сохранения момента импульса,
![]() ,
где J – момент инерции фигуриста
относительно оси вращения,
,
где J – момент инерции фигуриста
относительно оси вращения,
![]() –
угловая скорость его вращения вокруг
этой оси. Отсюда с учетом того, что
–
угловая скорость его вращения вокруг
этой оси. Отсюда с учетом того, что
![]() ,
где n
– частота вращения,
,
где n
– частота вращения,
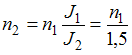 .
Кинетическая энергия тела, вращающегося
вокруг неподвижной оси, равна:
.
Кинетическая энергия тела, вращающегося
вокруг неподвижной оси, равна:
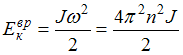 .
Тогда
.
Тогда
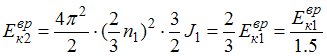 .
Таким образом, частота вращения фигуриста
и его кинетическая энергия уменьшатся
в 1,5 раза.
.
Таким образом, частота вращения фигуриста
и его кинетическая энергия уменьшатся
в 1,5 раза.
ЗАДАНИЕ N 6 Тема: Элементы специальной теории относительности
Полная энергия релятивистской частицы в 2 раза превышает ее энергию покоя. При этом скорость частицы равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Полная
энергия частицы, движущейся со скоростью
![]() ,
определяется соотношением
,
определяется соотношением
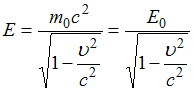 ,
где
,
где
![]() –
ее энергия покоя. Тогда
–
ее энергия покоя. Тогда
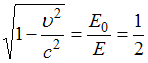 .
Отсюда
.
Отсюда
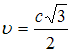 .
.
ЗАДАНИЕ N 7 Тема: Тепловое излучение. Фотоэффект
Наблюдается явление внешнего фотоэффекта. При этом с увеличением длины волны падающего света …
|
|
|
уменьшается величина задерживающей разности потенциалов |
|
|
|
увеличивается кинетическая энергия электронов |
|
|
|
увеличивается красная граница фотоэффекта |
|
|
|
увеличивается энергия фотонов |
Решение:
Согласно
уравнению Эйнштейна для фотоэффекта,
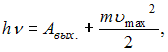 где
где
![]() энергия
падающего фотона,
энергия
падающего фотона,
![]() работа
выхода электрона из металла,
работа
выхода электрона из металла,
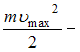 максимальная
кинетическая энергия электрона. Энергию
фотона можно выразить через длину волны:
максимальная
кинетическая энергия электрона. Энергию
фотона можно выразить через длину волны:
![]() ,
а максимальную кинетическую энергию
электронов – через величину задерживающей
разности потенциалов:
,
а максимальную кинетическую энергию
электронов – через величину задерживающей
разности потенциалов:
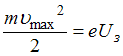 .
Тогда уравнение Эйнштейна запишется в
виде:
.
Тогда уравнение Эйнштейна запишется в
виде:
![]() .
Отсюда следует, что при увеличении длины
волны уменьшается энергия фотонов и
величина задерживающей разности
потенциалов (и кинетической энергии
электронов), поскольку красная граница
фотоэффекта определяется работой выхода
электронов из металла и не зависит от
длины волны падающего света.
.
Отсюда следует, что при увеличении длины
волны уменьшается энергия фотонов и
величина задерживающей разности
потенциалов (и кинетической энергии
электронов), поскольку красная граница
фотоэффекта определяется работой выхода
электронов из металла и не зависит от
длины волны падающего света.