Тема 6. Метод Фурье.

Лекция 1. Разделение переменных.

Рассматриваемые вопросы.

1. Решение основных краевых задач методом Фурье.

2. Интеграл Пуассона.

3. Внешняя и внутренняя задачи Дирихле.

Пусть ω – круг радиуса R с центром в начале координат, а S – окружность (граница области ω.

Рассмотрим задачу Дирихле

(1)

Перейдем к полярным координатам по формулам

Оператор Лапласа в полярных координатах

и задача (1) эквивалентна задаче

(2)

Будем искать решение в виде:

Подставим в уравнение Лапласа

или

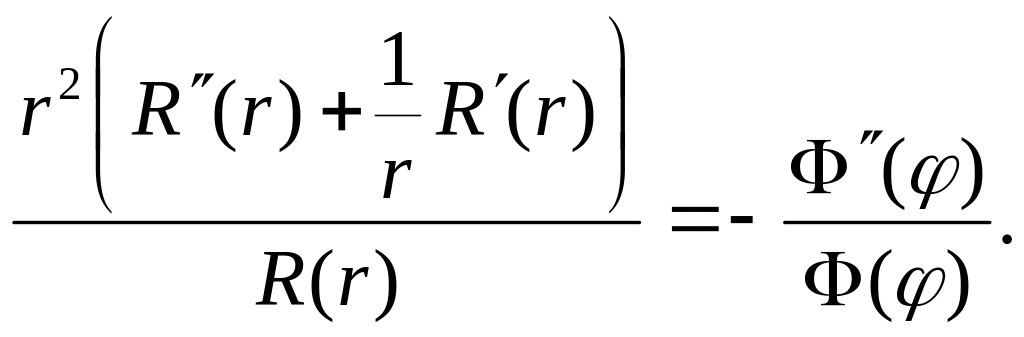
Следовательно, и левая и правая части этого равенства суть const (можно показать, что эта постоянная положительна)

Угловая функция Ф(φ) должна быть периодической. Учитывая это, получим задачу Штурма-Лиувилля.

(3)

Равенство (3) возможно лишь в случае

Для искомой функции R(r) получаем уравнение

Будем искать решение этого уравнения в виде , тогда

Если же n=0, то . Как нетрудно проверить имеет своими решениями и lnr. Таким образом, мы получаем набор функций, гармонических в круге

Если предположить, что ряд

(4)

можно дифференцировать почленно, то его сумма также будет гармонической функцией.

Подберем коэффициенты этого ряда так, чтобы

Отсюда с учетом формул для коэффициентов Фурье следует:

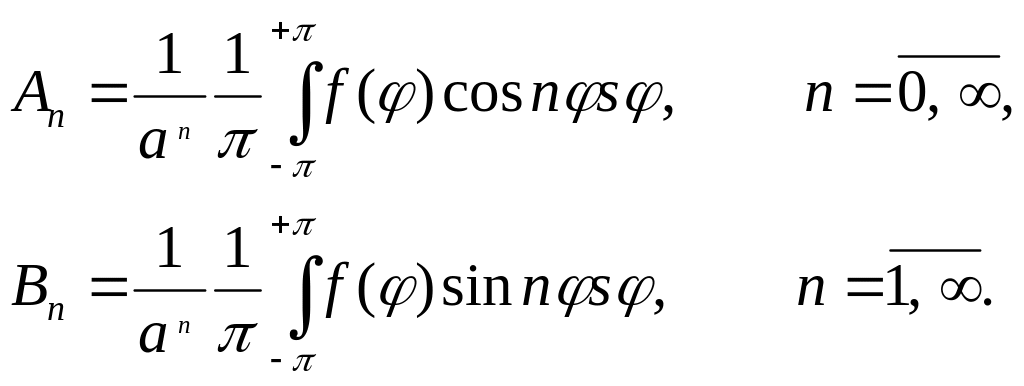
Замечание. Ряд (4) очевидно дает общий вид гармонической функции для круга r<a. Угловые функции и при этом не использовались, так как они при разрывны. Вместе с тем, если рассматривать область r>a (внешняя сторона круга), то общий вид гармонической функции для этой области будет задаваться рядом:

(5)

И, наконец, для кольца

(6)

Преобразуем теперь найденные решения к более удобному представлению

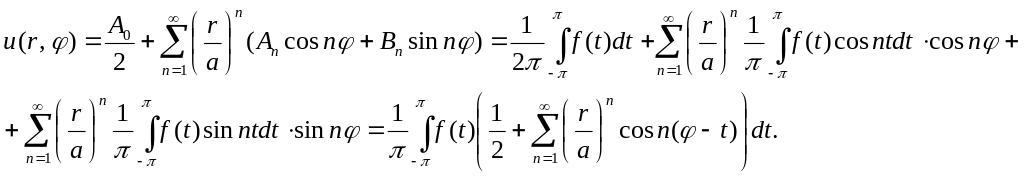
Перестановка операций суммирования и интегрирования законна, так как ряд

сходится равномерно по φ и t нутрии круга r<a. Найдем сумму этого ряда

Поэтому

(7)

Представление (7) известно как интеграл Пуассона.

Замечание. Среди двумерных областей, для которых задача Дирихле для уравнений Лапласа решается эффективно методом разделения переменных в декартовых координатах, можно отметить прямоугольник со сторонами параллельными осям координат и в, частности, полуполосу.

Тема 7. Теория потенциала.

Лекция 1. Теория потенциала.

Рассматриваемые вопросы.

1.Объемный и логарифмический потенциалы.

2. Поверхностные потенциалы.

3. Решение основных краевых задач методом потенциала.

Некоторые сведения из теории потенциала.

1. Объемный потенциал и его свойства.

Предположим, что в области распределен электрический заряд с плотностью Для нахождения потенциала такого электростатического поля разобьем область ω на элементарные части не имеющие общих внутренних точек. Допустим, что действие заряженной области равносильно действию точечного заряда Тогда потенциал электростатического поля в точке наблюдения можно найти по формуле:

При очевидно

(1)

Функцию (1) называют объмным или ньютоновским потенциалом.

Свойство 1. Объемный потенциал есть гармоническая функция по координатам точки во внешней области .

Если то (1) есть обычный тройной интеграл, функция имеет непрерывные производные любого порядка, интеграл поэтому производные по можно вычислять дифференцированием под знаком интеграла. В частности

так как если

Свойство 2. Объемный потенциал есть непрерывная функция по координатам точки во всем пространстве

Действительно, непрерывности в внешности вытекает из ее гармоничности. Пусть теперь точка а есть шар радиуса с центром в точке такой, что

Рассмотрим разность где точка

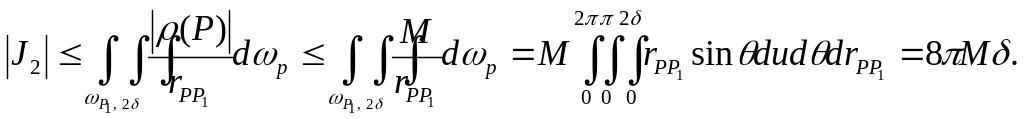
Для аналогично получаем

Будем считать, что δ фиксировано так, что

Оценим теперь Если то выбирая Р₁ достаточно близко к Р₀ получим

с помощью которого

А значит

Непрерывность во внутренних точках области ω объемного потенциала доказана.

Пусть теперь точка – границе области ω. Рассмотрим более широкую область и положим

Тогда

и точка Р₀ будет внутренней по отношению к Следовательно, потенциал в точке Р₀ непрерывен.

Свойство 3. Объемный потенциал имеет непрерывные производные первого порядка в Доказательство аналогично доказательству свойства 2.

Свойство 4. Если плотность имеет непрерывные производные первого порядка, то объемный потенциал имеет производные второго порядка в области ω и удовлетворяет уравнению Пуассона

(без доказательства).

Замечание 1. С помощью объемного потенциала решение задачи Дирихле для уравнения Пуассона может быть сведено к решению задачи Дирихле для уравнения Лапласа.

Замечание 2. В двумерном случае роль объемного потенциала играет так называемый логарифмический потенциал

Поверхностные интегралы простого и двойного слоя.

Пусть на некоторой достаточно гладкой поверхности S распределен заряд с плотностью Тогда потенциал электростатического поля в точке представляется в виде:

(2)

Функцию (2) называют потенциалом простого слоя. Перечислим некоторые свойства этого потенциала.

1). Потенциал простого слоя есть гармоническая вне S функция.

2). Потенциал простого слоя есть непрерывная во всем пространстве функция.

3). Нормальная производная потенциала простого слоя терпит разрыв при переходе через поверхность S.

Потенциалом двойного слоя называется выражение

где ν(Р) – есть плотность распределения дипольного момента, а – внутренняя нормаль к S.

4). Потенциал двойного слоя есть гармоническая вне S функция.

5). Потенциал двойного слоя терпит разрыв при переходе через поверхность S.

6). Потенциал двойного слоя может быть представлен в виде:

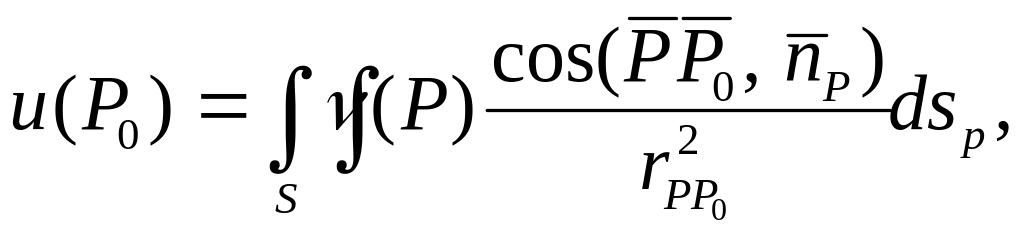
Аналогично могут быть введены криволинейные интегралы простого и двойного слоя с аналогичными свойствами.

Замечание. С помощью потенциала двойного слоя решение задачи Дирихле можно свести к решению уравнения Фредгольма второго рода относительно неизвестной функции