
Колебания и волны введение
Две революции, совершенные математикой в физике: в 1822г. ТЕОРЕМА ФУРЬЕ (впервые доказана Фурье, в наше время остается предметом исследований и находит многочисленные применения в науке). Любое (повторяющееся) движение можно рассматривать как результат наложения простых гармонических движений. Любую волну независимо от ее формы, можно рассматривать как сумму простых гармонических волн. И в 1924г. - ДУАЛИЗМ ДЕ БРОЙЛЯ (гипотеза де Бройля получила развитие и служит основанием современной атомной физики). Любая движущаяся частица (электрон, атом, нейтрон, футбольный мяч, даже квант света) ведет себя в одних случаях как размытая волна, а в других — как частица.
Мы уже знакомы с простым гармоническим движением - обычной составной частью всех колебаний. Оно представляет собой весьма распространенный и очень важный тип движения. Оно играет значительную роль в акустике, а также в современной атомной теории волн и частиц.
Изучение волнового движения составляет большой раздел физики и служит базой для таких прикладных исследований, как изучение океанских воли и землетрясений, исследования в области акустики и многие другие. Изучение волнового движения приобрело еще большее значение, когда «оказалось», что свет — это волны, и когда гипотеза де Бройля произвела новую революцию в физике.
ГЛАВА 1
ВОЛНЫ В УПРУГИХ СРЕДАХ
«Путешествующему на корабле кажется, что океан состоит из волн, а не из воды».
Э. С. Эддингтон
(Кэмбридж, 1929 г.)
§ 1. Образование и распространение волн в упругой среде
Начнем с определения упругой среды. Как можно заключить из названия упругая среда это такая среда в которой действуют силы упругости. Применительно к нашим целям, добавим, что при любом возмущении этой среды (не эмоциональной бурной реакции, а отклонении параметров среды в каком то месте от равновесных) в ней возникают силы, стремящиеся вернуть нашу среду в первоначальное равновесное состояние. При этом мы будем рассматривать протяженные среды. Насколько протяженные это мы уточним в дальнейшем, а пока будем считать, что этого достаточно. Например представим себе длинную пружину, закрепленную с обоих концов. Если в некотором месте пружины сжать несколько витков, то сжатые витки будут стремиться расжаться, а соседние витки, которые оказались растянутыми, будут стремиться сжаться. Таким образом наша упругая среда – пружина будет стараться придти в первоначальное спокойное (невозмущенное) состояние.
Газы, жидкости, твердые тела представляют собой упругие среды. Важным в предыдущем примере является то обстоятельство, что сжатый участок пружины действует на соседние участки, или по ученому говоря, передает возмущение. Похожим образом и в газе, создавая в каком то месте например область пониженного давления, соседние области, стремясь выровнять давление, будут передавать возмущение уже своим соседям, те в свою очередь своим и так далее.
Пара слов о физических величинах. В термодинамике как правило состояние тела определяется общими для всего тела параметрами, давлением газа, его температурой и плотностью. Теперь же нас будет интересовать локальное распределение этих величин.
Если колеблющееся тело (струна, мембрана и т. д.) находится в упругой среде (газ как мы уже знаем это упругая среда), то оно приводит в колебательное движение соприкасающиеся с ним частицы среды. Вследствие этого в прилегающих к телу элементах среды возникают периодические деформации (например, сжатия и разряжения). При этих деформациях в среде появляются упругие силы, стремящиеся вернуть элементы среды к первоначальным состояниям равновесия; благодаря взаимодействию соседних элементов среды упругие деформации будут передаваться от одних участков среды к другим, более удаленным от колеблющегося тела.
Т аким
образом, периодические деформации,
вызванные в каком-нибудь месте упругой
среды, будут распространяться в среде
с некоторой скоростью, зависящей от ее
физических свойств. При этом частицы
среды совершают колебательные движения
около положений равновесия; от одних
участков среды к другим передается
только состояние деформации.
аким
образом, периодические деформации,
вызванные в каком-нибудь месте упругой
среды, будут распространяться в среде
с некоторой скоростью, зависящей от ее
физических свойств. При этом частицы
среды совершают колебательные движения
около положений равновесия; от одних
участков среды к другим передается
только состояние деформации.
Когда рыба «клюет» (дергает за крючок), то от поплавка по поверхности воды разбегаются круги. Вместе с поплавком смещаются соприкасающиеся с ним частицы воды, которые вовлекают в движение ближайшие к ним другие частицы и так далее.
Такое же явление происходит с частицами натянутого резинового шнура, если один его конец привести в колебание (рис. 1.1).
Распространение колебаний в среде называют волновым движением Рассмотрим подробнее, как возникает волна на шнуре. Если зафиксировать положения шнура через каждые 1/4 Т (Т - это период, с которым на рис.1.1 колеблется рука) после начала колебаний его первой точки, то получится картина, показанная на рис. 1.2, б—д. Положение а соответствует началу колебаний первой точки шнура. Десять его точек помечены цифрами, а пунктирные прямые показывают, где находятся одни и те же точки шнура в разные моменты времени.
Ч ерез
1/4 Т после начала колебания точка 1
занимает крайнее верхнее положение, а
точка 2 только начинает свое движение.
Поскольку каждая последующая точка
шнура начинает свое движение позже
предыдущей, то в промежутке 1—2 точки
располагаются, как показано на рис. 1.2,
б. Еще через 1/4 Т точка 1 займет положение
равновесия и будет двигаться вниз, а
верхнее положение займет точка 2
(положение в). Точка 3 в этот момент только
начинает свое движение.
ерез
1/4 Т после начала колебания точка 1
занимает крайнее верхнее положение, а
точка 2 только начинает свое движение.
Поскольку каждая последующая точка
шнура начинает свое движение позже
предыдущей, то в промежутке 1—2 точки
располагаются, как показано на рис. 1.2,
б. Еще через 1/4 Т точка 1 займет положение
равновесия и будет двигаться вниз, а
верхнее положение займет точка 2
(положение в). Точка 3 в этот момент только
начинает свое движение.
За целый период колебания распространяются до точки 5 шнура (положение д). По окончании периода Т точка 1, двигаясь вверх, начнет свое второе колебание. Одновременно с ней начнет двигаться вверх и точка 5, совершая свое первое колебание. В дальнейшем эти точки будут иметь одинаковые фазы колебаний. Совокупность точек шнура в интервале 1—5 образует волну. Когда точка 1 закончит второе колебание, на шнуре вовлекутся в движение еще точки 5—10, т. е. образуется вторая волна.
Если проследить за положением точек, имеющих одинаковую фазу, то будет видно, что фаза как бы переходит от точки к точке и движется вправо. Действительно, если в положении б фазу 1/4 имеет точка 1, то в положении в эту же фазу имеет точка 2 и т. д.
Волны, в которых происходит перемещение фазы с определенной скоростью, называют бегущими. При наблюдении за волнами видно именно распространение фазы, например движение гребня волны. Отметим, что все точки среды в волне колеблются около своего положения равновесия и вместе с фазой не перемещаются.
Итак:
Процесс распространения колебательного движения в среде называется волновым процессом или просто волной.
В зависимости от характера возникающих при этом упругих деформаций различают волны продольные и поперечные. В продольных волнах частицы среды колеблются вдоль линии, совпадающей с направлением распространения колебаний. В поперечных волнах частицы среды колеблются перпендикулярно к направлению распространения волны. На рис. 1.3 показано расположение частиц среды (условно изображенных в виде черточек) в продольных (а) и поперечных (б) волнах.
Ж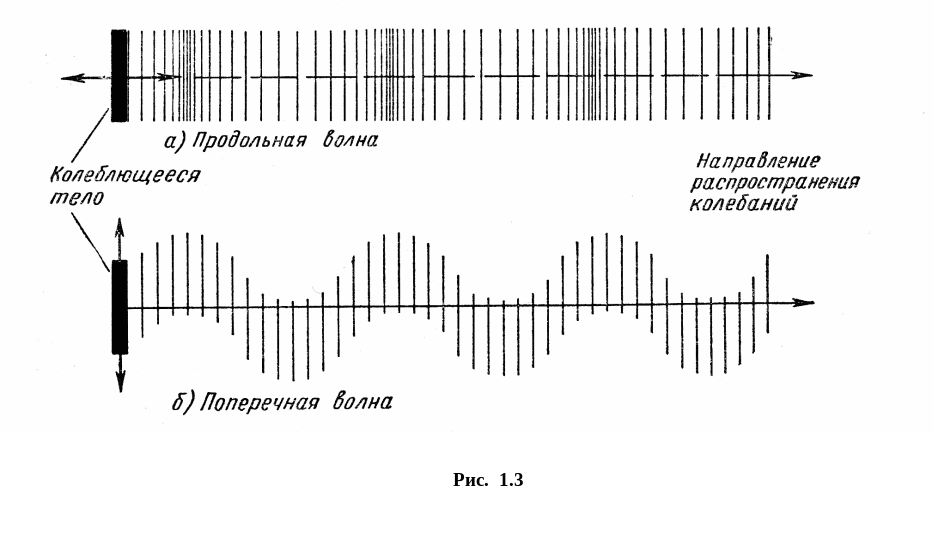 идкие
и газообразные среды не имеют упругости
сдвига и поэтому в них возбуждаются
только продольные волны, распространяющиеся
в виде чередующихся сжатий и разрежений
среды. Волны, возбуждаемые на поверхности
поды, являются поперечными: они обязаны
своим существованием земному тяготению.
В твердых телах могут быть вызваны и
продольные и поперечные волны; частным
видом поперечных воли являются крутильные,
возбуждаемые в упругих стержнях, к
которым приложены крутильные колебания.
идкие
и газообразные среды не имеют упругости
сдвига и поэтому в них возбуждаются
только продольные волны, распространяющиеся
в виде чередующихся сжатий и разрежений
среды. Волны, возбуждаемые на поверхности
поды, являются поперечными: они обязаны
своим существованием земному тяготению.
В твердых телах могут быть вызваны и
продольные и поперечные волны; частным
видом поперечных воли являются крутильные,
возбуждаемые в упругих стержнях, к
которым приложены крутильные колебания.
Предположим, что точечный источник волны начал возбуждать в среде колебания в момент времени t = 0; по истечении времени t это колебание распространится по различным направлениям на расстоянии ri =cit , где сi — скорость волны в данном направлении.
Поверхность, до которой доходит колебание в некоторый момент времени, называется фронтом волны.
Понятно, что фронт волны (волновой фронт) перемещается со временем в пространстве.
Форма фронта волны определяется конфигурацией источника колебаний и свойствами среды. В однородных средах скорость распространения волны везде одинакова. Среда называется изотропной, если эта скорость одинакова по всем направлениям. Фронт волны от точечного источника колебаний в однородном и изотропной среде имеет вид сферы; такие волны называются сферическими.
В неоднородной и не изотропной (анизотропной) среде, а также от неточечных источников колебаний фронт волны имеет сложную форму. Если фронт волны представляет собой плоскость и эта форма сохраняется по мере распространения колебаний в среде, то волну называют плоской. Малые участки фронта волны сложной формы можно считать плоской волной (если только рассматривать небольшие расстояния, проходимые этой волной).
П ри
описании волновых процессов выделяют
поверхности, в которых все частицы
колеблются в одинаковой фазе; эти
«поверхности одинаковой фазы» называются
волновыми, или фазовыми.
ри
описании волновых процессов выделяют
поверхности, в которых все частицы
колеблются в одинаковой фазе; эти
«поверхности одинаковой фазы» называются
волновыми, или фазовыми.
Ясно, что фронт волны представляет собой переднюю волновую поверхность, т.е. наиболее удаленную от источника, создающего волны, и волновые поверхности также могут быть сферическими, плоскими или иметь сложную форму в зависимости от конфигурации источника колебаний и свойств среды. На рис. 1.4 условно показаны: I — сферическая волна от точечного источника, II – волна от колеблющейся пластинки, III — эллиптическая волна от точечного источника в анизотропной среде, в которой скорость распространения волны с плавно изменяется по мере возрастания угла α, достигая максимума вдоль направления АА и минимума вдоль ВВ.
