Индивидуальная работа

Государственный комитет Российской Федерации

по высшему образованию

Санкт-Петербургский государственный электротехнический университет

Кафедра ИИСТ

Домашняя работа

Студент: Виноградов К. ãð. 6561

Преподаватель: Карабанов И.А.

Санкт-Петербург

Задача #3.

После пятикратного измерения сопротивления некоторого объекта с помощью равновесного моста вышел из строя гальванометр, используемый в качестве нуль-индикатора. После замены гальванометра измерения были продолжены и получены еще семь значений сопротивления. Можно ли объединять все полученные значения в один ряд, если обработка первых пяти измерений дала результаты кОм и Ом², а последующих семи измерений кОм и Ом² ?

Решение.

n₁=5 кОм Ом²

n₂=7 кОм Ом²

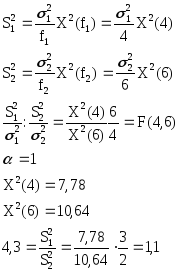
4,53 < 4,3 < 9,15

Ответ: Объединять нельзя.

Задача #4.

Косвенно измеряемая величина z связана с непосредственно измеряемыми аргументами функциональной зависимостью z=x+y. Восьмикратное измерение аргумента x дало результаты =2,10 и . Семикратное измерение аргумента y при известной дисперсии погрешности дало результат =1,16. Hайти результат измерения для z и доверительный интервал при P=0,9.

Решение.

z=x+y

x: n=8 =2,10

y: n=7 =1,16

Задача #5.

Косвенно измеряемая величина z связана с непосредственно измеряемыми аргументами функциональной зависимостью z=2x+3y. Восьмикратное измерение аргумента x дало результаты =2,10 и . Тринадцатикратное измерение аргумента y дало результаты =1,16 и. Hайти результат измерения для z и оценку доверительного интервала при P=0,9. Закон распределения погрешностей аргументов - нормальный.

Решение.

z=2x+3y

x: n=8 =2,10

y: n=13 =1,16

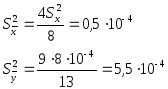
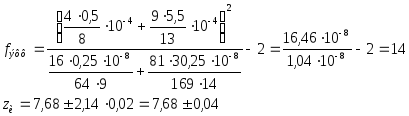
Задача #6.

Для уменьшения помехи, являющейся источником случайных погрешностей, были приняты определенные меры, которые могли только ослабить помеху. Можно ли считать, что принятые меры

1. действительно уменьшили дисперсию помехи

2. не внесли систематической погрешности,

если до принятия мер шестикратное измерение параметра некоторого объекта дало результаты =273 и =21, а после принятия мер восьмикратное измерение того же параметра дало результаты =270 и =6?

Решение.

n=6 =273 =21

n=8 =270 =6

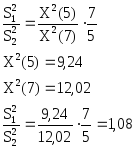
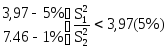
на уровне знам. a=0,1 примим гипотезу об одинаковой дисперсии.

Ответ: нет систематических погрешностей.

Задача #7.

Картинка с двумя последовательно соединенными резисторами R1 и R2

Hайти значение и доверительный интервал (P=0,95) для выходного напряжения делителя, если измерения напряжений вольтметром дали

значения U=0,62В, U1=2,10В, U2=6,01В при дисперсии погрешности вольтметра В². Закон распределения погрешностей - нормальный.

Решение.

Задача #10.

Серия из тринадцати измерений некоторой величины x_и дала оценку результата измерения =10,1 при оценке дисперсии ряда =6,5. Вторая серия из восьми измерений заведомо той же величины дала оценки =11,3 и=1,6. Дать окончательную оценку измеряемой величины без указания доверительного интервала.

Решение.

n=13 =10,1 =6,5

n=8 =11,3 =1,6

по Фишеру дисперсии одинаковые.

Ответ: =10,96

Задача #1.

Косвенно измеряемая величина связана с непосредственно измеряемыми аргументами функциональной зависимостью z=2x+y. Двухкратное измерение аргумента x при дисперсии погрешности дало результат = 2,15. Однократное измерение аргумента y при дисперсии погрешности дало результат = 1,70. Найти доверительный интервал для при P=0,9. Закон распределения погрешностей аргументов - равномерный.

Задача #2.

При косвенном измерении сопротивления по формуле R=U/I используется

источник питания, напряжение которого можно регулировать в пределах

от 0 до 15В. Для измерения напряжения имеется вольтметр класса точности 1,0 с пределами измерений 3-1-30В. Для измерения тока есть миллиамперметр с пределом измерения 1 мА класса точности 1,5. С какой минимальной относительной погрешностью можно получить результат измерения сопротивления, если измеряемый резистор имеет сопротивление около 30 кОм?

Задача #8.

Случайная величина x распределена по равномерному закону с дисперсией . Hайти доверительный интервал для измеряемой величины, если по двум измерениям было получено =5,12. Доверительная вероятность P=0,9.

Задача #9.

При испытании измерительного усилителя была проведена корректировка нуля, затем для определения коэффициента усиления было пять раз установлено входное напряжение, равное 1В, и по пяти соответствующим значениям выходного напряжения было найдено =5,2 В, затем пять раз было установлено входное напряжение, равное 8В, и получено соответствующее =39,8 В. В техническом паспорте записано: коэффициент усиления K=5,0ñ0,1. Соответствует ли коэффициент усиления паспортным данным, если дисперсия погрешности средства измерения входного напряжения составляет В², а выходного напряжения -

В². Закон распределения погрешностей - нормальный. P=0,95.