2.5. Интегрирование лнду второго порядка с постоянными коэффициентами и правой частью специального вида
Определение 2.6. ЛНДУ второго порядка называется ДУ вида
,
(2.7)
где
заданные функции,
непрерывные на промежутке
.
Уравнение вида
,
левая часть которого совпадает с левой частью ЛНДУ (2.7), называется соответствующим однородным уравнением.
Теорема 2.5 (структура общего решения ЛНДУ).
Общее решение ЛНДУ имеет вид
,
где
общее решение
соответствующего ему однородного
уравнения, а
одно из частных
решений уравнения.
Определение 2.7. ЛНДУ второго порядка с постоянными коэффициентами называется ДУ вида
,
(2.8)
где и постоянные действительные числа.
Согласно теореме 2.5. общее решение ЛНДУ второго порядка (2.8) представляет собой сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.
Для нахождения частного решения неоднородного уравнения с постоянными коэффициентами разработан метод, который называется методом неопределенных коэффициентов. Этот метод используется, если правая часть уравнения (2.8) имеет так называемый «специальный вид»:
I вид:
,
где
,
многочлен степени
.
или
II вид:
,
где
,
и
многочлены степени
и
соответственно.
Суть метода неопределенных коэффициентов состоит в следующем: по виду правой части уравнения (2.8) записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют ее в уравнение (2.8) и из полученного тождества находят значения коэффициентов.
Случай 1. Правая часть уравнения (2.8) имеет вид
,
(2.9)
где , многочлен степени .
В этом случае частное решение находится в виде
,
(2.10)
где
число, равное
кратности
как корня характеристического уравнения
(т.е.
число, показывающее,
сколько раз
является корнем характеристического
уравнения), а
многочлен степени
,
записанный с неопределенными коэффициентами
.
Случай 2. Правая часть уравнения (2.8) имеет вид
,
(2.11)
где , и многочлены степени и соответственно.
В этом случае частное решение находится в виде
,
(2.12)
где
число, равное
кратности
как корня характеристического уравнения
,
а
и
многочлен степени
с неопределенными коэффициентами,
наивысшая степень
многочленов
и
,
т.е.
.
Надо отметить, что форма (2.12) сохраняется
и в случае, когда
или
.
Алгоритм решения лнду второго порядка с постоянными коэффициентами и специальной правой частью
Для соответствующего однородного уравнения составляем и решаем характеристическое уравнение.
Составляем общее решение однородного уравнения.
С учетом специальной левой части составляем частное решение .
С помощью метода неопределенных коэффициентов находим частное решение .
По формуле получаем общее решение уравнения.
Алгоритм решения ЛНДУ можно использовать для линейных ДУ -го порядка с постоянными коэффициентами и правой частью специального вида.
Пример 2.7. Решить ЛНДУ второго
порядка:
.
Решение. 1) Рассмотрим однородное
уравнение
Составляем и решаем характеристическое уравнение:
.
Находим корни характеристического
уравнения:
и
.
2) Общее решение примет вид
.
3) Правая часть уравнения имеет вид
,
где
и
.
Так как
является однократным корнем
характеристического уравнения, а
многочлен первой
степени, то частное решение определяется
формулой
,
где
и
,
т.е.
.
4) С помощью метода неопределенных
коэффициентов находим частное решение.
Итак,
.
Далее находим
и
:
Подставляем , и в исходное уравнение, получаем:
Далее
.
Сокращаем обе части последнего тождества
на
и,
приравнивая коэффициенты при одинаковых
степенях
в левой и правой частях, получаем систему
уравнений:
.
5) Теперь можно записать общее решение исходного уравнения:
.
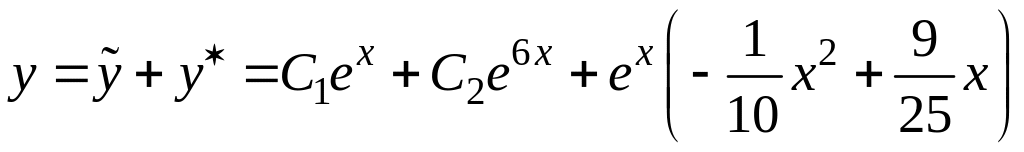