Основные понятия скалярного поля
4.1. Скалярное поле
Предположим, что в каждой точке
некоторой области
задано значение скалярной физической
величины
,
т.е. такой величины, которая полностью
характеризуется своим числовым значением.
Например, это может быть температура
точек неравномерно нагретого тела,
плотность распределения электрических
зарядов в изолированном наэлектризованном
теле, потенциал электрического поля и
т.д. При этом
называется скалярной функцией точки,
записывается это так
.
Область
,
в которой определена функция
,
может совпадать со всем пространством,
а может являться некоторой его частью.
Определение 4.1. Если в области задана скалярная функция точки , то говорят, что в этой области задано скалярное поле.
Будем считать, что скалярное поле стационарное, т.е. величина не зависит от времени .
Если физическая величина векторная, то ей будет соответствовать векторное поле, например, силовое поле, электрическое поле напряженности, магнитное поле и др.
Если скалярное поле отнесено к системе
координат
,
то задание точки
равносильно заданию ее координат
,
и тогда функция
можно записать в обычном виде функции
трех переменных:
.
Рассмотрим точки области
,
в которых функция
имеет постоянное значение
,
т.е.
.
Совокупность этих точек образует
некоторую поверхность. Если возьмем
другое значение
,
то получим другую поверхность. Эти
поверхности называются поверхностями
уровня.
Определение 4.2. Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция принимает постоянное значение, т.е.
.
В курсе физики при рассмотрении поля потенциала поверхности уровня называют обычно эквипотенциальными поверхностями (т.е. поверхности равного потенциала).
Если скалярное поле плоское, т.е. изучается
распределение значений величины в
какой-то плоской области, то функция
зависит от двух переменных, например,
и
.
Линиями уровня этого поля будут линии
уровня функции
,
т.е.
.
В прикладных науках часто употребляются линии уровня для представления изучаемой функции двух независимых переменных. Так, например, рассматривая высоту точки местности над уровнем моря как функцию двух переменных – координат точки, на карты наносят линии уровня этой функции. Они называются в топологии горизонталями. С помощью сети горизонталей удобно следить за изменением высоты местности. В метеорологии пользуются сетями изотерм и изобар (линий одинаковых средних температур и линий равных средних давлений), являющимися линиями уровня температуры и давления как функции координат точки местности.
Пример 4.1. Построить в плоскости
линии уровня функции
.
4.2. Производная по направлению
Важной характеристикой скалярного поля является скорость изменения поля в заданном направлении.
Пусть задано скалярное поле, т.е. задана
функция
,
и точка
.
Будем предполагать, что функция
непрерывна и имеет непрерывные производные
по своим аргументам в области
.
Проведем из точки
вектор
,
направляющие косинусы которого
.
На векторе
,
на расстоянии
от его начала, рассмотрим точку
.
Тогда
.
.
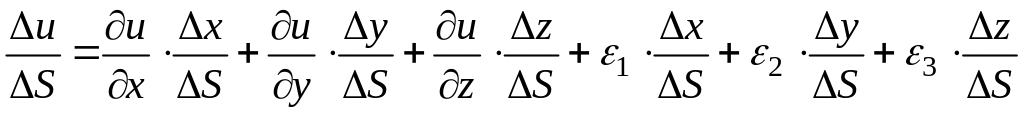Учитывая, что
,
то полученное равенство будет иметь
следующий вид:
.
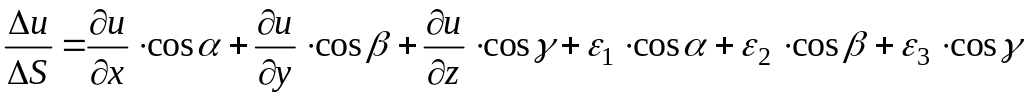Перейдем к пределу при
.
Определение 4.3. Предел отношения
при
называется производной от функции
в точке
по направлению вектора
и обозначается
,
т.е.
.
Итак, если функция
дифференцируемая, то производная от
функции в точке
по направлению вектора
находится по следующей формуле:
,
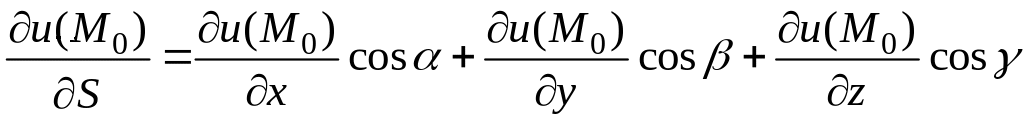(4.1)
где
направляющие
косинусы вектора
.
В случае функции двух переменных , т.е. когда поле плоское, формула (4.1) примет следующий вид:
,
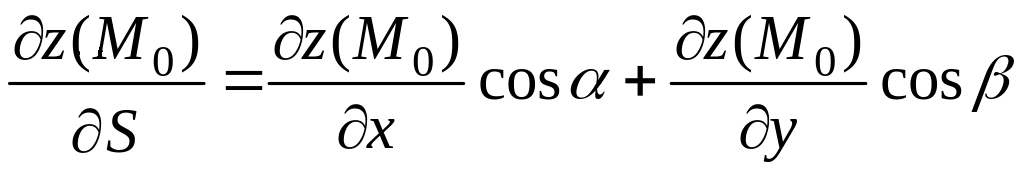(4.2)
где
.
Подобно тому, как частные производные
характеризуют скорость изменения
функции
в направлении осей координат, так и
производная по направлению
будет являться скоростью изменения
функции
в
точке
по направлению вектора
.