2.4. Производная сложной функции. Полная производная
Пусть
функция двух
переменных
и
,
каждая из которых является функцией
независимой переменной
,
т.е.
.
В этом случае функция
является сложной функцией одной
независимой переменной
,
а переменные
и
будут промежуточными переменными.
Теорема 2.2. Если
функция,
дифференцируемая в точке
,
и
дифференцируемые
функции независимой переменной
,
то производная сложной функции
вычисляется по формуле:
.
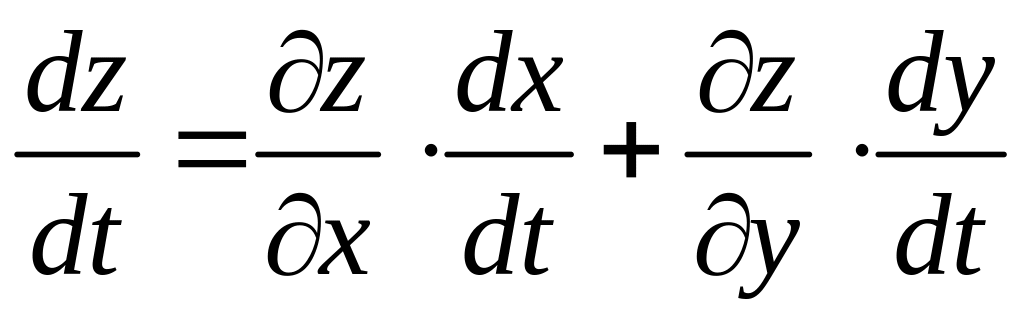(2.9)
Доказательство. Дадим независимой
переменной
приращение
.
Тогда функции
получат приращения
и
соответственно. Они, в свою очередь,
вызовут приращение
функции
.
Так как по условию функция дифференцируема в точке , то ее полное приращение можно представить в виде
,
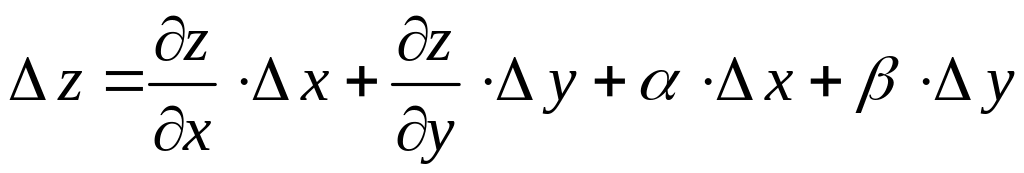где
и
при
.
Разделим выражение
на
и перейдем к пределу при
.
Тогда
и
в силу непрерывности функций
(по условию они дифференцируемые).
Получаем:
.
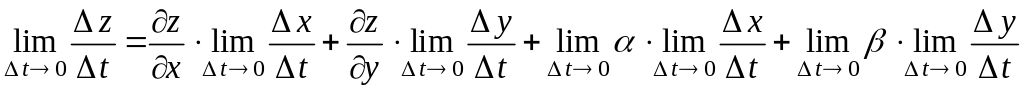Далее
,
или
.
Частный случай:
,
где
,
т.е.
сложная функция
одной независимой переменной
.
Этот случай сводится к предыдущему,
причем роль переменной
играет
.
Согласно формуле (2.9) имеем:
,
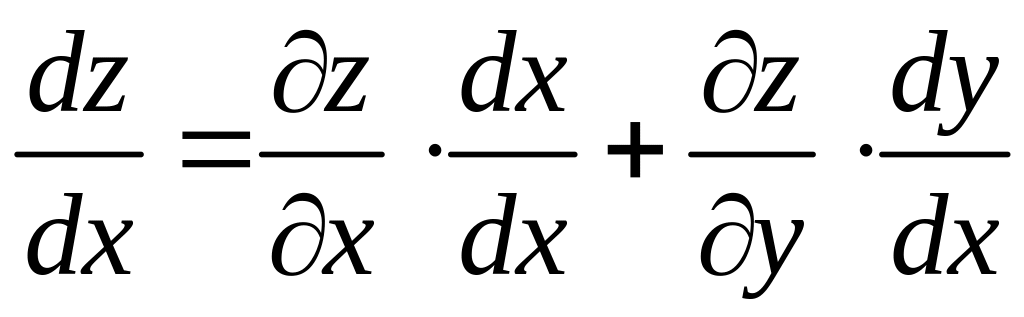или
.
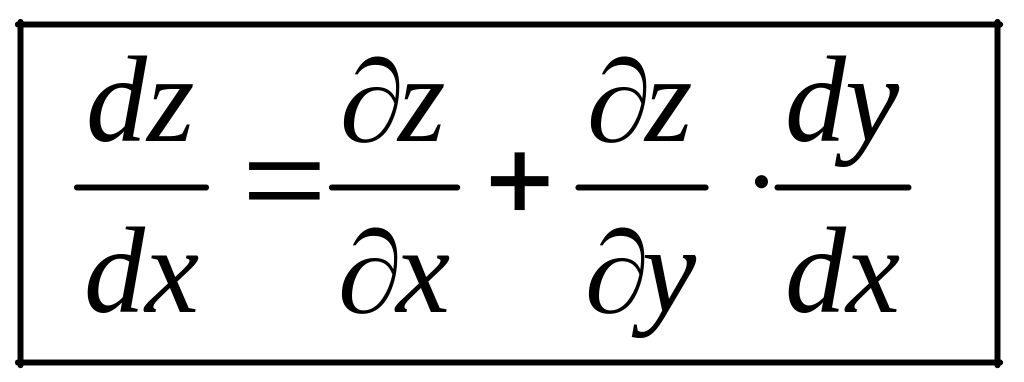(2.10)
Формула (2.10) называется формулой полной производной.
Общий случай:
,
где
.
Тогда
сложная функция
независимых переменных
и
.
Ее частные производные
и
можно найти по следующим формулам:
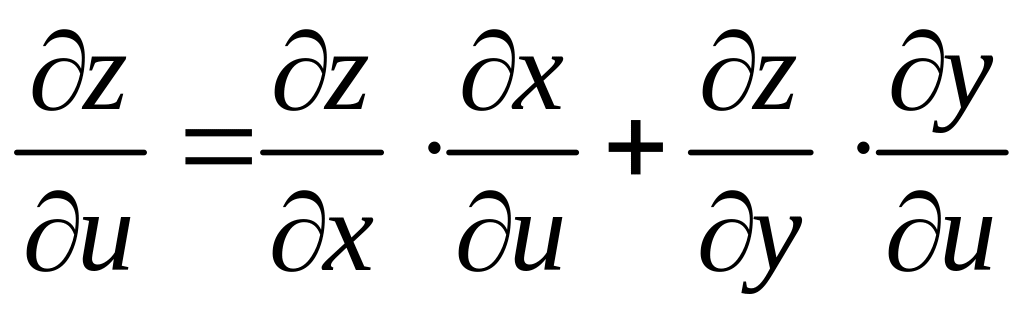и
.
(2.11)
Пример 2.7. Найти
,
если
.
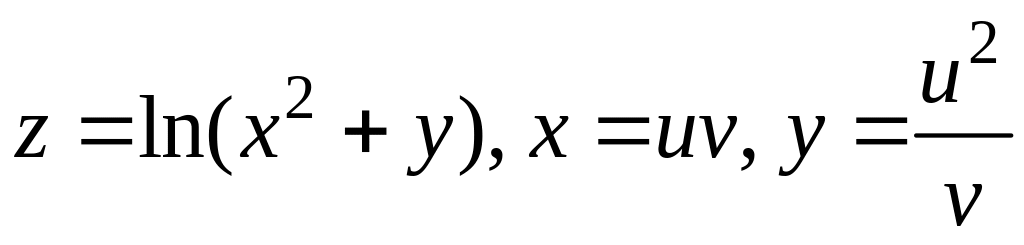Решение. Используя формулу (2.11), найдем :
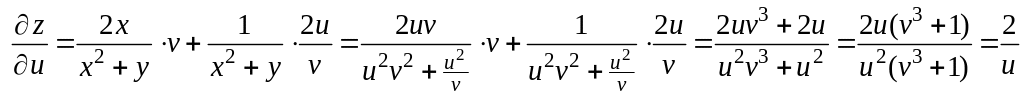
Надо отметить, что формулы (2.11) можно обобщить для случая большего числа переменных.
Используя правило дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности: полный дифференциал функции сохраняет один и тот же вид независимо от того, является ли аргументы независимыми переменными или функциями независимых переменных.
2.5. Дифференцирование неявной функции
Функция от двух переменных называется
неявной, если она задается
уравнением
,
неразрешенным относительно
.
Для вычисления частной производной
(или
)
надо зафиксировать
и дифференцировать уравнение
,
имея в виду, что
зависит от
.
По правилу дифференцирования сложной
функции получаем:
,
т.е.
.
Откуда
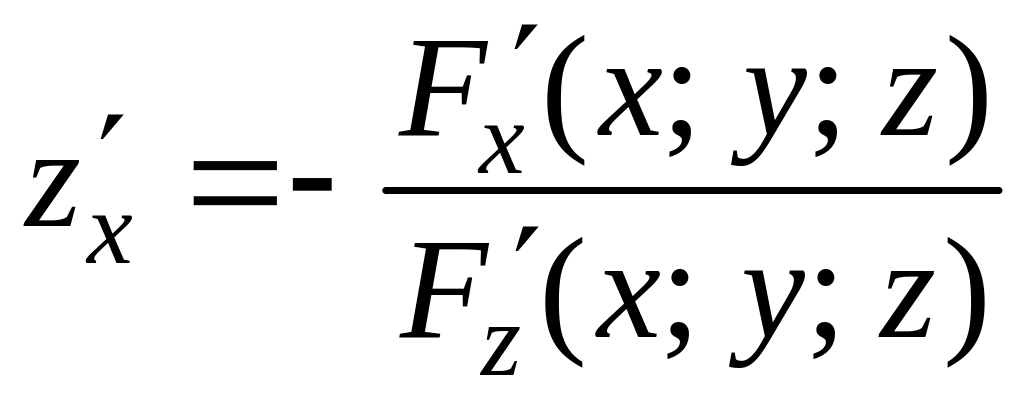или
.
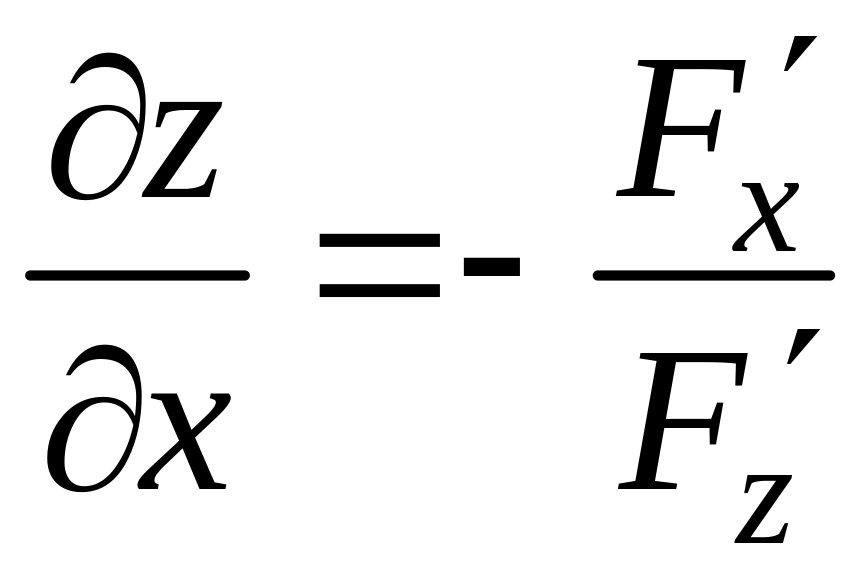(2.12)
Аналогично
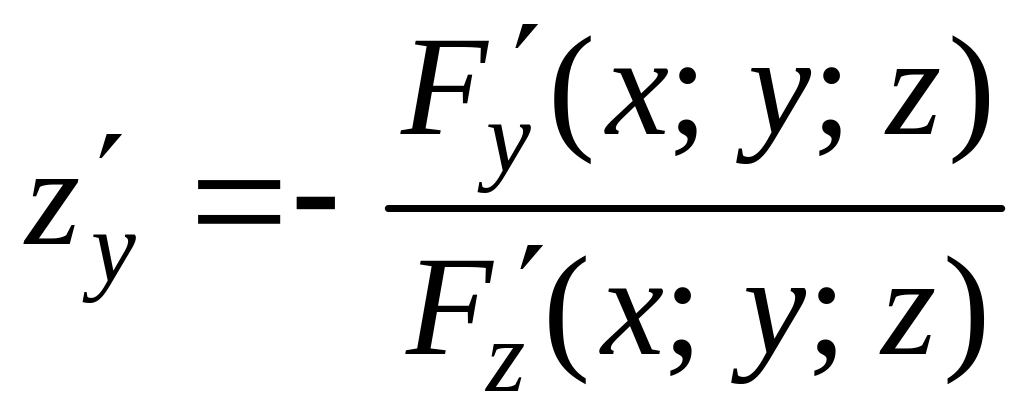или
.
(2.13)
Если хотим, чтобы эти производные принимали определенное значение, то надо требовать, чтобы выполнялось, так называемое, условие существования неявной функции
.
Пример 2.8. Найти частные производные функции, заданной уравнением:
.
Решение. Здесь
.
Далее находим
.
По формулам (2.12) и (2.13) получаем:
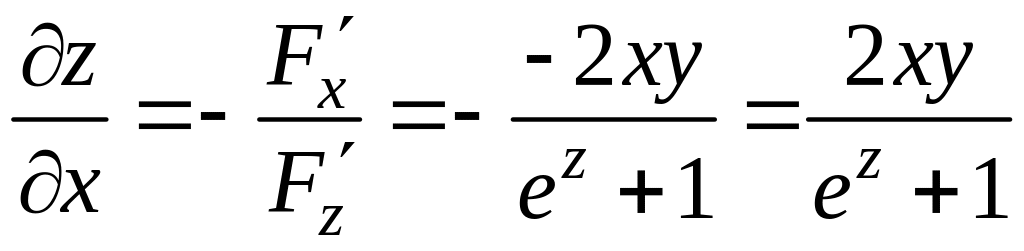и
.
И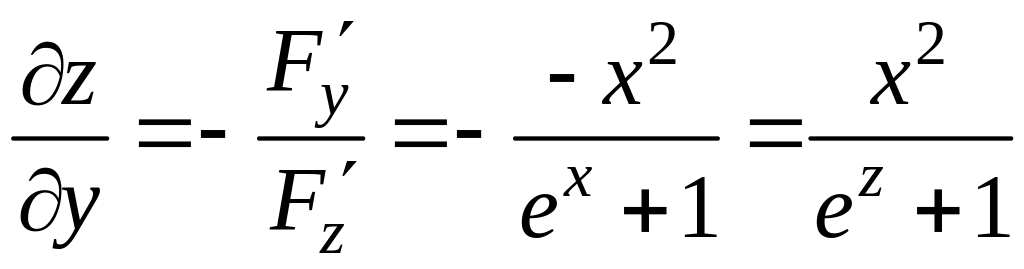сследование фнп
3.1. Касательная плоскость и нормаль к поверхности
Пусть имеем поверхность, заданную уравнением вида .
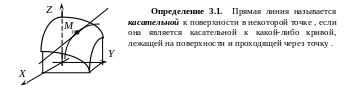
Так как через точку проходит бесчисленное число различных кривых, лежащих на поверхности, то и касательных к поверхности, проходящих через эту точку будет, вообще говоря, бесчисленное множество.
Введем понятие об особых и обыкновенных точках поверхности .
Если в точке
все три производные
равны нулю или хотя бы одна из этих
производных не существует, то точка
называется особой точкой
поверхности. Если в точке
все три производные
существуют и непрерывны, причем хотя
бы одна из них отлична от нуля, то точка
называется обыкновенной точкой
поверхности.
Теперь сформулируем теорему, которую примем без доказательства.
Теорема 3.1. Все касательные прямые к данной поверхности в ее обыкновенной точке лежат в одной плоскости.
Заметим, что в особых точках поверхности может не существовать касательной плоскости. В таких точках касательные прямые к поверхности могут не лежать в одной плоскости. Так, например, вершина конической поверхности является особой точкой. Касательные к конической поверхности в этой точке не лежат в одной плоскости (они сами образуют коническую поверхность).
Если уравнение поверхности задано в
неявном виде
и
,
то уравнение касательной плоскости в
точке
имеет вид:
.
(3.1)
Если поверхность задана уравнением , то уравнение касательной плоскости в точке к данной поверхности имеет вид:
.
(3.2)
Определение 3.3. Прямая, проведенная через точку поверхности перпендикулярно к касательной плоскости, называется нормалью к поверхности.
Если уравнение поверхности задано в неявном виде , то каноническое уравнение нормали в точке имеет вид:
.
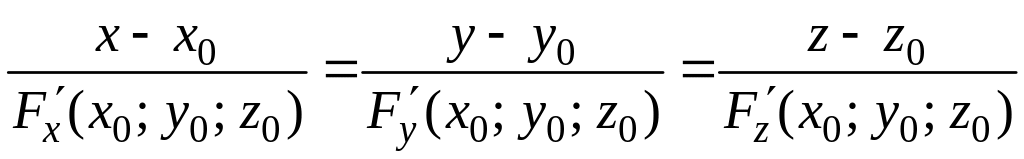(3.3)
Если поверхность задана уравнением , то каноническое уравнение нормали в точке имеет вид:
.
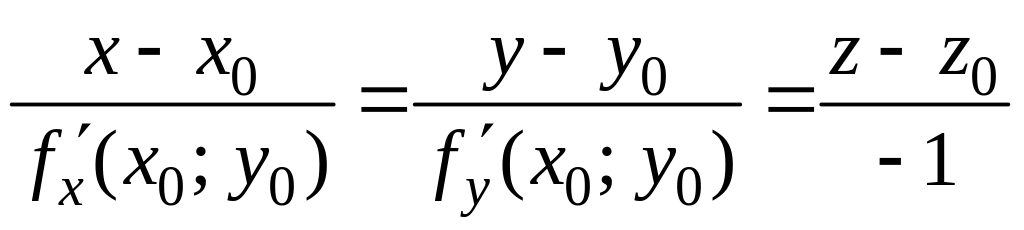(3.4)
Пример 3.1. Найти уравнение касательной
плоскости и уравнение нормали к
поверхности
в точке
Решение. Вычисляем значения частных производных в точке :
,
,
.
Подставляя их в уравнения (3.1) и (3.3), получаем соответственно уравнение касательной плоскости
,
и каноническое уравнение нормали
.