3.2. Экстремум функции двух переменных

Понятие максимум, минимум, экстремум функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной. Пусть функция определена в некоторой области , точка .

Определение 3.4. Точка называется точкой максимума , если существует такая -окрестность точки , что для каждой точки , отличной от , из этой окрестности выполняется неравенство

.

Определение 3.5. Точка называется точкой минимума , если существует такая -окрестность точки , что для каждой точки , отличной от , из этой окрестности выполняется неравенство

.

Значение функции в точке максимум (минимум) называется максимум (минимум) функции. Максимум и минимум функции называют ее экстремумами.

Отметим, что, в силу определения, точка экстремума лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер; значение функции в точке сравнивается с ее значениями в точках, достаточно близких к . В области функция может иметь несколько экстремумов или не иметь ни одного.

Рассмотрим условия существования экстремума функции.

Теорема 3.2 (необходимое условие экстремума).

Если точка является точкой экстремума функции , то или хотя бы одна из этих производных не существует.

Доказательство. Зафиксируем одну из переменных. Положим, например, . Тогда получим функцию , которая является функцией одной переменной. Эта функция имеет экстремум (максимум или минимум) при . Следовательно, согласно необходимому условию экстремума функции одной переменной, , т.е. или не существует.

Аналогично можно показать, что или не существует.



Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции, но позволяет находить эти значения в тех случаях, в которых заранее уверены в существовании максимума или минимума. В противном случае требуется дополнительное исследование.

Например, функция имеет частные производные , которые обращаются в нуль при . Но эта функция при указанных значениях не имеет ни максимума, ни минимума. Действительно, эта функция равна нулю в начале координат и принимает в как угодно близких точках от начала координат как положительные, так и отрицательные значения. Следовательно, значение нуль не является ни максимумом, ни минимумом.

Например, функция имеет экстремум в точке , но не имеет в этой точке частных производных.

Геометрический смысл: равенства означают, что в точке экстремума функции касательная плоскость к поверхности, изображающей функцию , параллельная плоскости Oxy, т.к. уравнение касательной плоскости есть .

Определение 3.6. Точки, в которых хотя бы одна частная производная равна нулю или не существует, то такие точки называются критическими точками.

Если речь идет о точках, в которых частные производные первого порядка равны нулю, то такие точки называются стационарными точками.

Для исследования функции в критических точках сформулируем достаточное условие экстремума функции двух переменных. Следующую теорему примем без доказательства.

Теорема 3.3 (достаточное условие экстремума). Пусть функция имеет непрерывные частные производные до третьего порядка включительно в некоторой области, содержащей стационарную точку . Вычислим в точке значения . Обозначим

.

Тогда:

1. если , то функция имеет экстремум в точке :

   • максимум, если ;

   • минимум, если ;

2. если 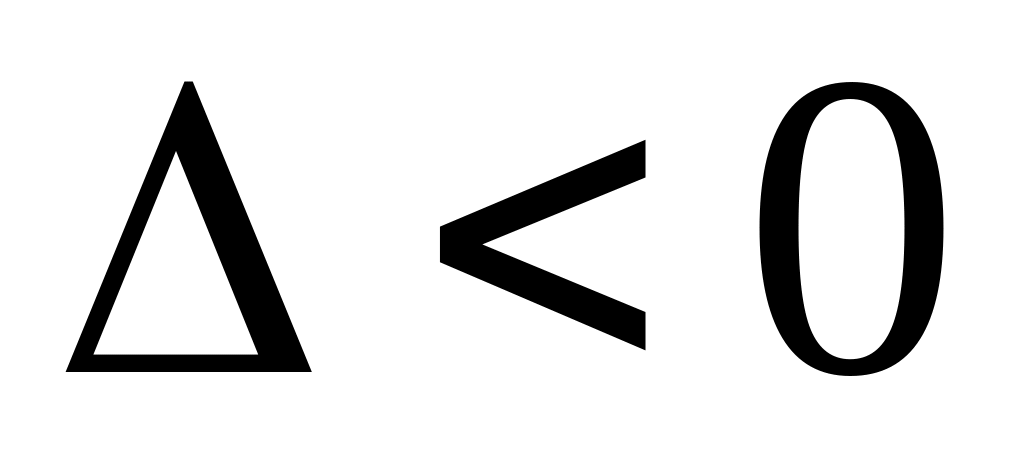, то функция не имеет экстремума в точке ;

3. если , то экстремум в точке может быть, а может и не быть. Необходимы дополнительные исследования.

Пример 3.2. Найти экстремум функции .

Решение. 1) Найдем частные производные первого порядка:

.

Чтобы найти стационарные (критические) точки, составляем и решаем систему уравнений:

 или .

Таким образом, получаем две стационарные точки и .

2) Находим частные производные второго порядка:

.

3) Исследуем характер каждой стационарной точки.

а) В точке имеем

Тогда

.

Так как , то в точке функция имеет локальный максимум.

.

б) В точке имеем

.

Тогда . Проведем дополнительное исследование. Значение функции в точке равно нулю, т.е. . Можно заметить, что при ; при . Значит, в окрестности точки функция принимает как отрицательные, так и положительные значения. Следовательно, в точке функция экстремума не имеет.



3.3. Наибольшее и наименьшее значения функции

в замкнутой области

Пусть функция определена и непрерывна в ограниченной замкнутой области . Тогда она достигает в некоторых точках своего наибольшего и наименьшего значений (так называемый глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области , или в точках, лежащих на границе области.

Правило нахождения наибольшего и наименьшего значений

в замкнутой области

1. Найти все критические точки функции, принадлежащие , и вычислить значения функции в них.

2. Найти наибольшее и наименьшее значения функции на границах области.

3. Сравнить все найденные значения функции и выбрать из них наибольшее и наименьшее .

Пример 3.3. Найти наибольшее и наименьшее значения функции в замкнутой области , ограниченной линиями: .

Решение. 1) Строим замкнутую область , ограниченную линиями: .

 , , , .

Таким образом, получаем четыре стационарные точки, ни одна из которых не принадлежит области .

3) Исследуем функцию на границе области, состоящей из участков и .

а) на границу : .

Тогда получаем функцию от одной переменной : . Находим критические точки: .

 .

Далее .

б) на границу : .

Тогда получаем функцию от одной переменной : . Находим критические точки: .

 и .

Далее .

в) на границу : .

Тогда получаем функцию от одной переменной : . Находим критические точки: .

 .

Далее .

г) на границу : .

Тогда получаем функцию от одной переменной :

.

Находим критические точки: .

 . Значит, на границе критических точек нет.

4) Находим значения функции в вершинах области: . Выше были найдены значения функции и , что соответствует значениям функции в точках и . Поэтому находим значения функции в точках и :

;

.

Из всех полученных значений функции выбираем наибольшее и наименьшее:

; .

