16. Тригонометричні та обернені тригонометричні ф-ції дійсн. Змінної (озн., неп-сть та ін. Вл-сті, графік).

Озн.: Косинусом гострого кута прямок. трик-ка наз. віднош. прилег. катета до гіпотенузи. Синусом – відношення протил. катета до гіпотенузи. Тангенсом – віднош. протилежного катета до прилеглого. Котангенсом – віднош. прилеглого катета до протилежного.

arcsin числа а , а є[-1, 1] наз. таке число b з проміжка [-п/2, п/2], синус якого = а. arccos ч-ла а, а є[-1, 1] наз. ч-ло b з відрізка [0, п], соsb=a. arctg ч-ла а наз таке ч-ло b з інтервала (-п/2, п/2), tgb=a. arcctg a наз. ч-ло b з інтервала (0, п), ctgb=a.

Похідні: (sinx)'=cosx.

Дов.: ∆f=sin(х₀+∆х)-sin(х₀)=2sin(∆х/2)·cos(х₀+∆х/2). f'= ,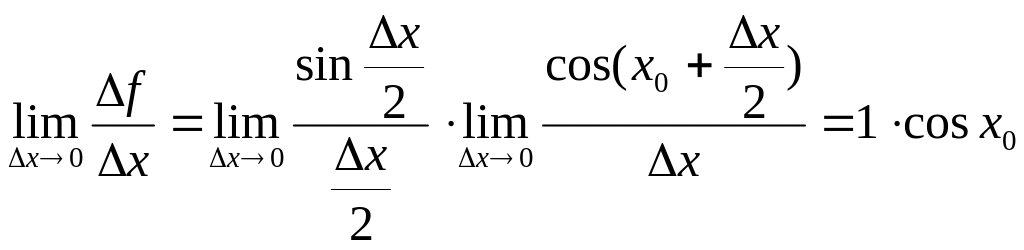

- перша чудова границя. (sinx₀)'=cosx₀. Довед.

(cosx)'=-sinx, (tgx)'=1/cos²x, (ctgx)'=1/sin²x, (arcsinx)'=1/ , (arccosx)'=-1/ , (arctgx)'=1/(1+x²), (arcctgx)'=-1/(1+x²).

Розклад в ряди:

17. Поняття метричного простору. Приклади метр. Пр-рів. Збіжні послідовності в метр. Пр-рах.

Метрикою на даній множині Х наз. ф-я 2-х аргументів ρ(х,у), для якої викон. 3 аксіоми: 1) акс. невідємності: ρ(х,у) 0 для х,уЄХ. При чому, ρ(х,у)=0  x=y. 2) симетричності: ρ(х,у)=ρ(у,х) х,уЄХю 3) трикутника: х,у, zЄХ : ρ(х,z) ρ(х,у)+ρ(y,z). Метр. пр-р: мн-на, яка наділена метрикою.

Прикл. МП: 1. Rⁿ- n-вим. арифм. пр-р. 2. С_{[a, b]} – пр-р непер. ф-й на [a, b] , ρ(х,у)= |y(t)-x(t)|. 3. Пр-р квадратичних сумовних послідовностей l₂. Точками простору є такі послідовності дійс. ч-л, для яких ряд, складений з квадратів є збіжним. ρ(х,у)= - метрика.

Озн.: Фіксуємо т. а пр-ру Х і фіксуємо певний додат. радіус r. Відкритою кулею з ц. в т. а, рад-са r в даному пр-рі наз. мн-на всіх таких т. цього простору, відст. від яких до даної т. а є меншою r. Якщо r, то куля замкнена.

ε- околом даної т. наз. відкрита куля з ц. в цій т. радіуса ε.

Посл-сть х_n даного простору наз. збіжною до т. а цього ж пр-ру, якщо для дов. ε-околу т. а знайдеться такий номер n₀ , що для всіх нарут. ч-л n з виконання умови n>n₀ => що x_n попадає в ε-окіл т. а. Інакше кажучи, викон. нер-сть ρ(x_n,а)<ε.

18. n-вим. евклідів простір Rⁿ як узагальнення просторів R¹, R², R³.

Метрикою на даній множині Х наз. ф-я 2-х аргументів ρ(х,у), для якої викон. 3 аксіоми: 1) акс. невідємності: ρ(х,у) 0 для х,уЄХ. При чому, ρ(х,у)=0  x=y. 2) симетричності: ρ(х,у)=ρ(у,х) х,уЄХю 3) трикутника: х,у, zЄХ : ρ(х,z) ρ(х,у)+ρ(y,z). Метр. пр-р: мн-на, яка наділена метрикою.

Поняття функ­ції однієї змінної — цілком природно, за аналогією, узагальнюється на довільну кількість п змінних з одночасним переходом від простору R² (площини) до п-вимірного простору Rⁿ. Подамо далі докладне теоретичне обґрунтування такого узагальнення. Множину, елементами якої є всі можливі набори впорядкованих n дійсних чисел, позначають Rⁿ. У цій множині означують поняття відстані між будь-якими двома її елементами. Відстань між елементами і , подається у вигляді ρ(х,у)= .(1)

Озн. Множина Rⁿ із введеною на ній відстанню називається n-вимірним простором Rⁿ, число n — розмірністю цього простору. Елемент  Î Rⁿ називається точкою простору Rⁿ, число х_і, , — і-ю координатою цієї точки. Точки n-вимірного простору Rⁿ утворю­ють і-ту координатну вісь простору. Точка 0 = (0, 0, …, 0) називається початком координат. Простір R¹ з елементами х = х₁ — числова пряма. Простори R² і R³ з елементами х = (х_1, х₂) і х = (х₁, х₂, х₃) являють собою відповідно площину і тривимірний простір.

У просторі Rⁿ можна означити поняття суми елементів і добутку елемента на дійсне число: якщо то (2)

Як відомо з лінійної алгебри, множина Rⁿ, в якій формулами (2) визначено суму її елементів та добуток будь-якого елемента на дійсне число, є лінійним векторним простором. Точку х = (х₁, х_2, …, х_n) простору Rⁿ називають вектором, а числа х_і, — його координатами в базисі е₁=(1,0,…,0),…, е_п=(0,0,…,1). У лінійному векторному просторі можна означити скалярний добуток (х, у), ставлячи у відповідність двом векторам х = (х₁, х₂, …, х_n) і у = (у₁, у₂, …, у_n)

число (3) Лінійний векторний простір Rⁿ, для елементів якого формулою (3) означено скалярний добуток, називається n-вимірним евклідовим простором.