11. Первісна та її властивості. Невизначений інтеграл. Основні способи інтегрування. Таблиця невизначених інтегралів від основних елементарних функцій.

Ф-я називається первісною для ф-ї , на деякому проміжку Х, якщо для усіх значень х Î Х виконується рівність = . Якщо - первісна для ф-ї , то й ф-я , де С - довільна стала, також є первісною для ф-ї , оскільки ( )′ = + С ′= + 0 = .

Означення. Сукупність усіх первісних ф-ї на проміжку Х називається невизначеним інтегралом ф-ї на цьому проміжку і позначається . Невизн. інтеграл інакше називають інтегралом Ньютона - Лейбніца. Якщо - одна з первісних функції , то за означенням = + С. Знак називається знаком невизначеного інтеграла, - підінтегральною ф-єю, а - підінтегр. виразом.

Операцію знаходження невизначеного інтеграла від функції називають інтегруванням цієї функції.

Основні властивості невизначеного інтеграла: 1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції. ( )′ = + С ′= . 2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу d( ) = d = d(x). 3. Невиз. Інт-л. від диференціала деякої функції дорівнює сумі цієї функції і довільної постійної = . 4. Сталий множник можна виносити за знак інтеграла, тобто, якщо k = const ¹ 0, то (Для доведення цієї властивості досить показати, що права чстина рівності є первісною підінтегральної функції ). 5. Невизначений інтеграл від суми (різниці) функцій дорівнює сумі (різниці) невизначених інтегралів від кожної функції, тобто . Доведення. .

СПОСОБИ ІНТЕГРУВАННЯ: Розкладання. Якщо f₁ i f₂ є інтегровними ф-ями і α₁ α₂ сталі множники, то інтеграл Метод підстановки В основі методу підстановки (методу заміни змінної) лежить формула диференціювання складеної функції. Якщо F ′( x) = f(x), хÎ(a, b), то для довільної диференційованої на проміжку (a, b ) функції x= j(t), де j(t) Î(a, b), якщо t Î(a, b ) маємо: (F(j(t)))′ = F ′( x) j′(t) = f(x) j′(t) = f(j(t)) j′(t). Таким чином, ,тобто

Інтегрування частинами Нехай функції і визначені й диференційовані на деякому проміжку Х. Тоді Дов. . Звідси маємо . Припустимо, що інтеграл існує. Тоді . Оскільки , то (1). Довільну сталу С включає в себе інтеграл . Формула (1) називається формулою інтегрування частинами.

Таблиця основних інтегралів

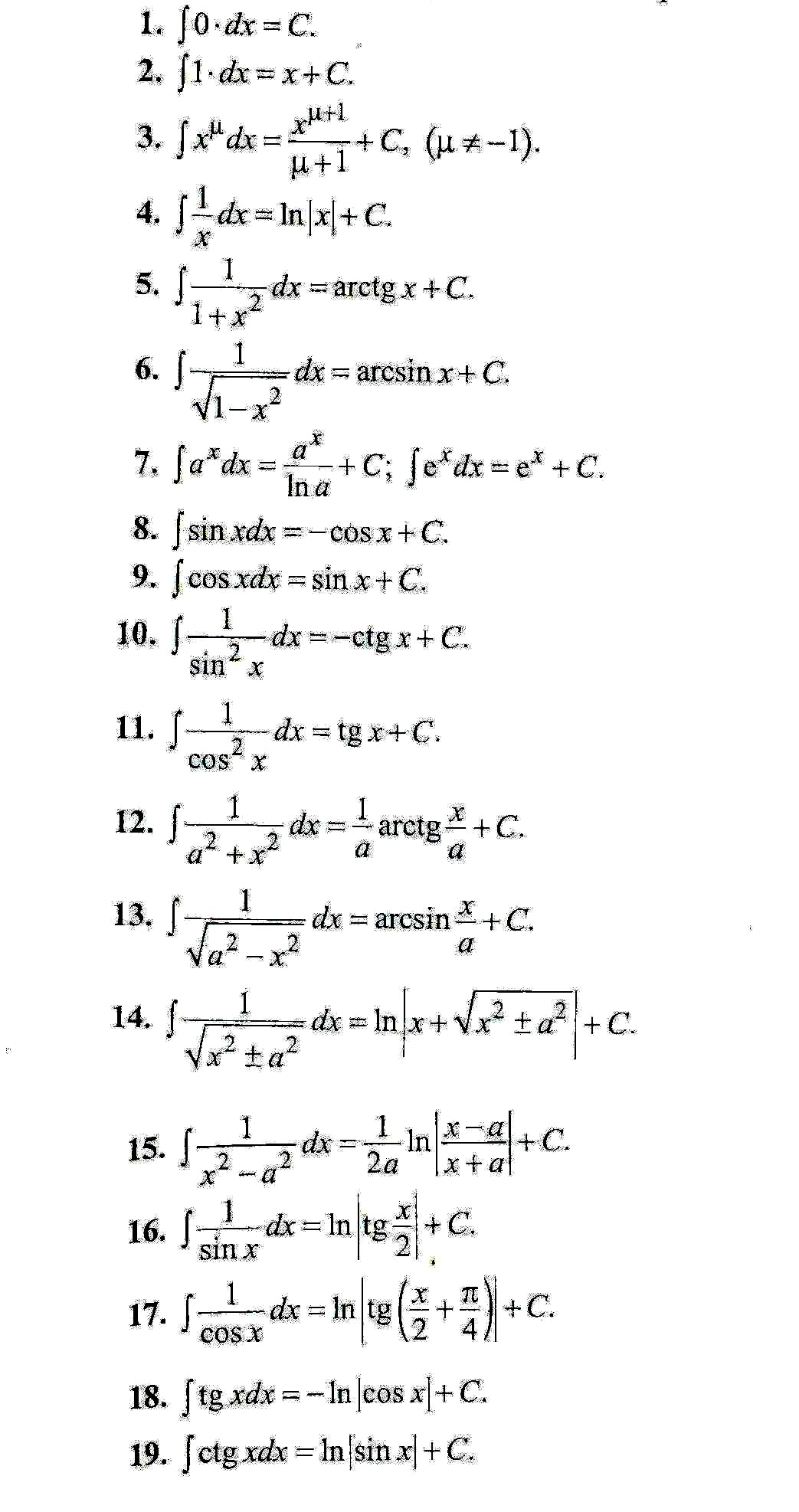
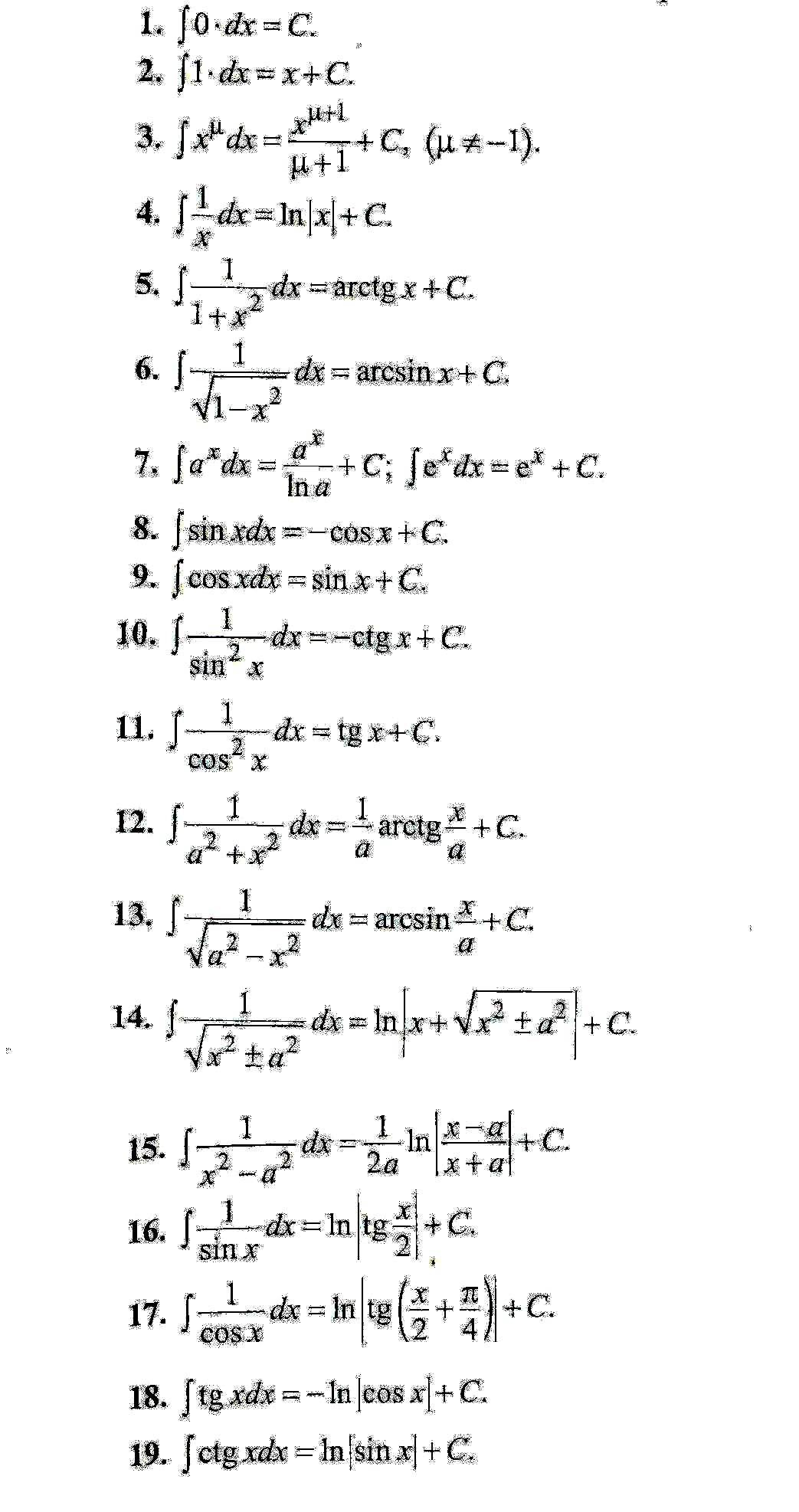
12. Інтеграл Рімана для функції однієї змінної. Основні властивості. Критерій інтегровності.

Нех. на на задана обмежена функція виконаємо T – розбиття точками . Позначимо через . Позначемо через . Вибиремо т. , . Оскільки - обмежена на , то вона обмедена на кожному відрізку , за теоремою про існування граней існує нижня і верхня грань множини значень функції на цьому відрізку:

, . Побудуємо суми: , - нижні та верхні суми Дарбу. Побудуємо суму =σ(τ ) – інрегральні суми Рімана.Число І називається границею інтегральної суми: , якщо Þ . Озн. Якщо існує скінченна границя інтегральної суми, за умови, що , то ця границя називається інтегралом Рімана, або визначеним інтегралом, а функція називається інтегрованою за Ріманом.

Властивості

Т: (необхідна ум. інтегровності) «Якщо функція - інтегрована на , то на цьому відрізку вона обмежена». ; 2) ; 3) ; 4) (адитивна: якщо f – інтегрована на ) .

Т. про критерій інтегровності. Для того, щоб ф-я f була інтегровною за Ріманом на даному [a,b] н. і д., щоб різниця між верх. і ниж. сумою Дарбу 0, коли _.

Дов. Н. Дано: f - інтегровна. Існує скінч. гран. сум Pімана. Познач. І. Тоді для достатньо дрібних розбиттів λ<δ, то |σ(τ )-I|<ε. Але тоді буде вірне:

I-ε< <I+ε, I-ε≤_S(T)≤¯S(T)≤I+ε

Але тоді відміність ¯S-_S≤2ε, коли .

Д. Розгл. для _S їх sup_S(T)=_I, для ¯S їх sup¯S(T)=¯I.Ствердж., що вони однакові. Припустимо, що це не так, тоді ¯I>_I. Але тоді ¯S(T)-_S(T)≥¯I-_I=const>0 не 0. Супер. із тим, що дано. Отже, ¯I=_I=I. |σ(τ )-I|≤¯S-_S0<ε. |σ(τ )-I|<ε, коли розб. достатньо мале. І – границія інтегр. сум Рімана. Ф-я інтегровна. дов.