
- •1. Потужність множини. Зчисленні множини та їх властивості. Множини n, z, q, r та їхні потужності.
- •2. Числова послідовність та її границя. Основні властивості границі. Границя обмеженої монотонної послідовності. Число е.
- •3. Дійсна функція дійсної змінної. Границя функції дійсної змінної у точці. Властивості границь.
- •4.Неперервність функції у точці. Приклади неперервних функцій. Властивості неперервних функцій.
- •5. Неперервність функції на множині. Властивості неперервних функцій на обмежених замкнених множинах.
- •6. Похідна функції дійсної змінної та її основні властивості. Диференційовність та диференціал функції.
- •7. Частинні похідні функції кількох змінних. Диференційовність та диференціал функції кількох змінних. Необхідна і достатня умова диференційовності.
- •8. Основні теореми диференціального числення. Теореми Ролля, Лагранжа, Коші, формула Тейлора.
- •9. Застосування диференціального числення до дослідження властивостей функцій. Умови сталості, монотонності, екстремумів.
- •Достатні умови існування екстремуму функції. Теорема. Нехай - критична точка функції , неперервна в точці і має похідну в усіх точках околу за виключенням, можливо самої точки . Тоді
- •10. Застосування диференціального числення до дослідження властивостей функцій. Опуклість і точки перегину.
- •11. Первісна та її властивості. Невизначений інтеграл. Основні способи інтегрування. Таблиця невизначених інтегралів від основних елементарних функцій.
- •12. Інтеграл Рімана для функції однієї змінної. Основні властивості. Критерій інтегровності.
- •13. Основні класи інтегровних за Ріманом функцій.
- •14. Розвиток поняття степеня з дійсним показником. Вл-сті степеня. Загальна степенева функція дійсної змінної (озн., власт., графік).
- •15. Показникова і логарифмічна функції дійсної змінної (озн., непер-сть та ін. Власт., графіки).
- •16. Тригонометричні та обернені тригонометричні ф-ції дійсн. Змінної (озн., неп-сть та ін. Вл-сті, графік).
- •17. Поняття метричного простору. Приклади метр. Пр-рів. Збіжні послідовності в метр. Пр-рах.
- •19. Числові ряди. Геометрична прогнесія та гармонійний ряд. Властивості збіжних рядів.
- •20. Додатні ряди. Основні ознаки збіжності додатних рядів. Ряди з довільнии членами . Абсолютно й умовно збіжні ряди.
- •21. Степеневі ряди. Інтерв. І рад. Зб-сті. Теор. Абеля та Адамара.
- •22. Ряд Тейлора для дійсної функції дійсної змінної. Розкладання у степеневий ряд основних елементарних функцій.
9. Застосування диференціального числення до дослідження властивостей функцій. Умови сталості, монотонності, екстремумів.
Т. Умова
сталості. Для
того, щоб диференційовна ф-ція
![]() в інтервалі
в інтервалі
![]() була постійною необхідно і досить, щоб
її похідна в цьому інтервалі дорівнювала
0.
була постійною необхідно і досить, щоб
її похідна в цьому інтервалі дорівнювала
0.
Т.
Монотонність.
Якщо функція
диференційована на інтервалі
![]() і
і
![]() на
,
то функція
на
,
то функція
![]() зростає (спадає).
зростає (спадає).
Дов.
Нехай для визначеності
![]() .
Візьмемо в інтервалі
дві довільні точки
.
Візьмемо в інтервалі
дві довільні точки
![]() такі, що
такі, що
![]() .
На відрізку
.
На відрізку
![]() функція
задовольняє умовам теореми Лагранжа.
Отже, існує точка
функція
задовольняє умовам теореми Лагранжа.
Отже, існує точка
![]() така,
що
така,
що
![]() .
Звідси
випливає, що за умов
.
Звідси
випливає, що за умов
![]() і
і
![]() маємо:
маємо:
![]() ,
тобто
,
тобто
![]() .
Для випадку
.
Для випадку
![]() доведення аналогічне.
доведення аналогічне.
Екстремуми
функції. Точка
![]() називається точкою локального максимуму
(мінімуму) функції
,
якщо існує
називається точкою локального максимуму
(мінімуму) функції
,
якщо існує
![]() -
окіл
-
окіл
![]() точки
такий, що
точки
такий, що
![]() для будь-якої відмінної від
точки
для будь-якої відмінної від
точки
![]() .
При цьому саме значення
.
При цьому саме значення
![]() називається локальним максимумом
(мінімумом) функції
.
Точки максимуму і мінімуму функції
називаються точками екстремуму або
екстремальними точками функції
.
називається локальним максимумом
(мінімумом) функції
.
Точки максимуму і мінімуму функції
називаються точками екстремуму або
екстремальними точками функції
.
Необхідна умова
існування локального екстремуму функції.
Якщо в точці
функція
має екстремум, то існує окіл
точки
,
в якому значення
є найбільшим або найменшим. Отже, якщо
в точці
функція
диференційована, то згідно теореми
Ферма
![]() Зазначимо,
що коли функція
диференційована в точці
і
Зазначимо,
що коли функція
диференційована в точці
і
![]() ,
то або
,
то або
![]() ,
тобто функція зростає, або
,
тобто функція зростає, або
![]() і функція спадає. Звідси
випливає, що функція
може мати екстремум лише в тих точках,
у яких її похідна
і функція спадає. Звідси
випливає, що функція
може мати екстремум лише в тих точках,
у яких її похідна
![]() рівна нулю, або не існує.
Точки, в
яких похідна функції
рівна нулю, називаються стаціонарними.
Стаціонарні точки й точки, в яких функція
визначена, але її похідна
не існує наз.
критичними.
Отже, для
того, щоб функція
мала в точці
екстремуму, необхідно, щоб ця точка була
критичною.
рівна нулю, або не існує.
Точки, в
яких похідна функції
рівна нулю, називаються стаціонарними.
Стаціонарні точки й точки, в яких функція
визначена, але її похідна
не існує наз.
критичними.
Отже, для
того, щоб функція
мала в точці
екстремуму, необхідно, щоб ця точка була
критичною.
Достатні умови існування екстремуму функції. Теорема. Нехай - критична точка функції , неперервна в точці і має похідну в усіх точках околу за виключенням, можливо самої точки . Тоді
якщо
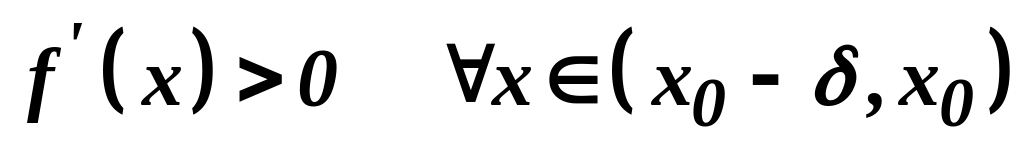 і
і
 ,
то точка
є точкою максимуму функції
.
,
то точка
є точкою максимуму функції
.якщо
 і
і
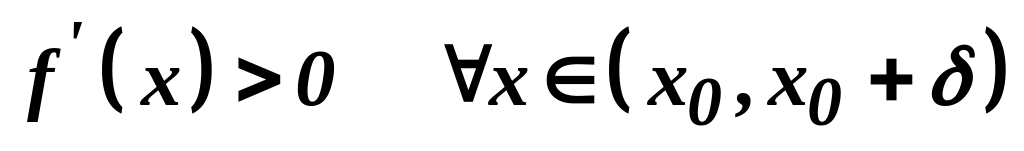 ,
то точка
є точкою мінімуму функції
.
,
то точка
є точкою мінімуму функції
.Якщо в околі має один і той же знак, то не є точкою екстремуму функції .
Друга
дост.
умова екстремуму:
Якщо ф-ція
![]() в
в
![]() -околі
стаціонарної точки
-околі
стаціонарної точки
![]() диференційовна і в цій точці має другу
похідну, відмінну від нуля, то
диференційовна і в цій точці має другу
похідну, відмінну від нуля, то
![]() - точка екстремуму, причому це точка
мінімуму, якщо
- точка екстремуму, причому це точка
мінімуму, якщо
![]() ,
і точка максимуму, якщо
,
і точка максимуму, якщо
![]() .
.
10. Застосування диференціального числення до дослідження властивостей функцій. Опуклість і точки перегину.
Нехай
функція
![]() визначена на інтервалі
визначена на інтервалі
![]() і в кожній точці цього інтервалу має
скінчену похідну. Тоді
в кожній точці
і в кожній точці цього інтервалу має
скінчену похідну. Тоді
в кожній точці
![]() графіка цієї функції можна провести
дотичну, не паралельну осі
графіка цієї функції можна провести
дотичну, не паралельну осі
![]() .
Крива, яка є графіком цієї функції,
називається гладкою.
Якщо крива, яка є графіком функції
.
Крива, яка є графіком цієї функції,
називається гладкою.
Якщо крива, яка є графіком функції
![]() ,
розміщена не нижче будь-якої дотичної
на інтервалі
,
то вона називається вгнутою
догори
або просто вгнутою
на цьому інтервалі або опуклою вниз .
Якщо крива, яка є графіком функції
,
розміщена не вище будь-якої дотичної
на інтервалі
,
то вона називається вгнутою
донизу
або просто опуклою
на цьому інтервалі або опуклою вгору.
,
розміщена не нижче будь-якої дотичної
на інтервалі
,
то вона називається вгнутою
догори
або просто вгнутою
на цьому інтервалі або опуклою вниз .
Якщо крива, яка є графіком функції
,
розміщена не вище будь-якої дотичної
на інтервалі
,
то вона називається вгнутою
донизу
або просто опуклою
на цьому інтервалі або опуклою вгору.
Точка
![]() називається точкою перегину
гладкої кривої
,
якщо існує
-окіл
точки
такий, що в інтервалах
називається точкою перегину
гладкої кривої
,
якщо існує
-окіл
точки
такий, що в інтервалах
![]() і
і
![]() крива
має опуклість різних напрямків. У
цьому випадку графік функції
в інтервалах
і
лежить по різні боки від дотичної,
проведеної в точці
.
крива
має опуклість різних напрямків. У
цьому випадку графік функції
в інтервалах
і
лежить по різні боки від дотичної,
проведеної в точці
.
Теорема.
Нехай функція
визначена на інтервалі
і в кожній точці цього інтервалу має
похідні до другого порядку включно.
Тоді, якщо
![]() у всіх точках
у всіх точках
![]() ,
то графік функції
на інтервалі
вгнутий (опуклий вниз), якщо ж
,
то графік функції
на інтервалі
вгнутий (опуклий вниз), якщо ж
![]() у всіх точках
,
то графік функції
на інтервалі
опуклий (опуклий вгору). Доведення.
в інтервалах
і
лежить по різні боки від дотичної,
проведеної в точці
.
Нехай
у всіх точках
,
то графік функції
на інтервалі
опуклий (опуклий вгору). Доведення.
в інтервалах
і
лежить по різні боки від дотичної,
проведеної в точці
.
Нехай
![]() .
Виберемо точку
.
Виберемо точку
![]() і покажемо, що графік функції
лежить не нижче дотичної, яка проходить
через точку
.
Щоб відрізняти ординату графіка функції
і ординату дотичної, останню будемо
позначати буквою
і покажемо, що графік функції
лежить не нижче дотичної, яка проходить
через точку
.
Щоб відрізняти ординату графіка функції
і ординату дотичної, останню будемо
позначати буквою
![]() .
Запишемо рівняння дотичної в точці
:
.
Запишемо рівняння дотичної в точці
:
![]() (1).
(1).
Оскільки
функція
має похідні до другого порядку включно,
то згідно формули Тейлора (при
![]() )
маємо:
)
маємо:
![]() (2)
де
(2)
де
![]() .
Віднімемо від рівності (2) рівність (1)
.
Віднімемо від рівності (2) рівність (1)
![]() .
Оскільки
.
Оскільки
![]() ,
то
,
то
![]() ,
тобто
,
тобто
![]() .
Отже, графік функції
у будь-якій, відмінній від
,
точці
лежить вище дотичної, проведеної до
нього в точці з абсцисою
.
Аналогічно
доводиться теорема для випадку
.
.
Отже, графік функції
у будь-якій, відмінній від
,
точці
лежить вище дотичної, проведеної до
нього в точці з абсцисою
.
Аналогічно
доводиться теорема для випадку
.
Установимо необхідну
умову існування точки перегину графіка
функції
.
Нехай функція
визначена і має неперервні похідні до
другого порядку включно на інтервалі
.
Тоді. Якщо в кожній точці
,
то графік функції
на інтервалі
вгнутий (опуклий вниз). Якщо
,
,
-
то графік опуклий (опуклий вгору).
Якщо на
інтервалі
![]() ,
то графік функції
точок перегину на цьому інтервалі не
має. Таким чином, точка
,
де
може бути точкою перегину графіка
функції
лише в тому випадку, коли
,
то графік функції
точок перегину на цьому інтервалі не
має. Таким чином, точка
,
де
може бути точкою перегину графіка
функції
лише в тому випадку, коли
![]() .
Отже, умова
є необхідною, для того, щоб точка
була точкою перегину графіка функції
.
.
Отже, умова
є необхідною, для того, щоб точка
була точкою перегину графіка функції
.
