КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Институт математики и механики им. Н.И. Лобачевского

А.С.Шкуро

Конспект лекций по математике-2

для студентов химического института

Учебное пособие

Казань – 2012

УДК 517

Печатается по решению учебно-методической комиссии

ФГАОУВПО «Казанский (Приволжский) федеральный университет»

Института математики и механики им. Н.И. Лобачевского

Протокол № от мая 2012 г.

заседания кафедры общей математики КФУ

Протокол № от мая 2012 г.

Научный редактор

докт. ф.-м. наук, проф. Н.Г.Гурьянов

Рецензенты:

докт. ф.-м. наук, проф. Ю.И.Бутенко,

канд. ф.-м. наук, доц. Е.П.Аксентьева

Шкуро А.С.

Конспект лекций по математике-2 для студентов химического института: учебное пособие / А.С. Шкуро. – Казань: Казанский (Приволжский) федеральный университет, 2012. – с.

Учебное пособие представляет собой конспект лекций по математике для студентов химического института, читаемых автором во втором семестре на протяжении ряда последних лет.

Пособие полностью соответствует ныне действующей программе курса математики для студентов-химиков, но может быть использовано студентами и других естественных специальностей, а также заинтересованными школьниками старших классов общеобразовательных школ.

© Казанский (Приволжский)

федеральный университет, 2012

Приложения производной

Лекция 1

Теорема Лагранжа о конечных приращениях

Если – дифференцируемая функция на некотором промежутке и - любые значения из этого промежутка, то где (1)

Доказательство. На графике функции проведем секущую АВ через точки и Будем перемещать эту секущую параллельно начальному положению до тех пор, пока она не превратится в касательную к графику нашей функции в некоторой точке его где Согласно нашему построению угловой коэффициент секущей равен угловому коэффициенту касательной поэтому откуда получается (1).

Следствие 1. Если производная функции равна нулю на некотором промежутке, то функция есть тождественная постоянная на этом промежутке.

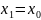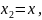Пусть при Полагая в (1) , где – некоторое фиксированное значение из и где – любое значение из этого интервала, будем иметь

. Отсюда если

Следствие 2. Если две функции имеют равные производные на некотором промежутке, то эти функции на рассматриваемом промежутке отличаются друг от друга самое большее на постоянное слагаемое.

Пусть при Тогда на этом промежутке имеем Следовательно, в силу следствия 1 функция для всех

Теорема Ролля о корнях производной

Между двумя последовательными корнями дифференцируемой функции всегда содержится по меньшей мере один корень ее производной.

Доказательство. Если - дифференцируемая функция и то из формулы (1) имеем

или так как то где

Замечание 1. Теорема имеет простую геометрическую интерпретацию. Между точками найдется по меньшей мере одна точка, в которой касательная к графику функции параллельна оси

Замечание 2. Теорему можно сформулировать и в более общем виде.

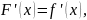
Если - функция, дифференцируемая на и то между найдется точка ξ , в которой производная равна нулю, то есть Действительно, случай рассмотрен выше; если то введем функцию тогда дифференцируема и т.е. для функции выполнены условия теоремы Ролля. Следовательно, существует точка ξ такая, что а значит и

Теорема Коши об отношении конечных приращений двух функций

Если - две дифференцируемые на функции, причем нигде внутри отрезка не обращается в нуль, то внутри отрезка найдется такая точка что

(2)

Доказательство. Определим число равенеством:

(3)

Отметим, что т.к. в противном случае равнялось бы и тогда по теореме Ролля производная обращалась бы в нуль внутри отрезка, что противоречит условию теоремы. Составим вспомогательную функцию

Заметив, что функция на отрезке удовлетворяет всем условиям теоремы Ролля, заключаем, что существует такое значение что Но следовательно,

откуда Подставляя значение в (3), получим (2).

Замечание. Теорему Коши нельзя доказать, как это может показаться с первого взгляда, применением теоремы Лагранжа к числителю и знаменателю дроби: . Действительно, мы получили бы в этом случае (после сокращения на 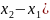формулу

в которой Но так как , вообще говоря, то полученный результат, очевидно, не дает еще теоремы Коши.