Приклад 1

У мене є список з Musik-файли Wich названі:

Ім'я, first_name - CDTitle.mp3 але я хотів, щоб вони

Ім'я ім'я - CDTitle.mp3

Example 1

I have a list of musik-files wich are named:

Name, first_name - CDTitle.mp3 but I like to get them

firstname name - CDTitle.mp3

13. Арифметичні та алгебраїчні обчислення в системі Mathematica: арифметичні операції, основні елементарні функції, перетворення алгебраїчних виразів, правила заміни.

Арифметичні та алгебраїчні обчислення в системі Mathematica: арифметичні операції, основні елементарні функції, перетворення алгебраїчних виразів, правила заміни.

Арифметичні операції:

+ - * / ^ Sqrt[x]

Арифметичні функції:

Plus[x,y,…], Times[x,y,…] (добуток чисел),Divide[x,y] (ділення x, на y), Mod[x,y] (остача ділення від x, на y).

Цілочислові дільники Divisors[n]

DivisorSigma[k,n] повертає суму піднесених в степінь k позитивних дільників чила.

ExtendedGCD[n,m]повертає найбільш=ший спільний дільник чисел n та m.

GCD[n1,n2,…] – повертає найбільший спільний дільник цілих чисел.

LCM[n1,n2,…] - повертає найменше спільне кратне цілих чисел n1,n2.

Round[x]- заокруглення до найблищого цілого.

Floor[x] – найбільше ціле число яке неперевищує x.

Quotient[n,m]- повертає заокруглене ціле число n/m ?яке неперевищує значення n/m.

Factorial[n]- повертає факторіал числа.

Prime[n] повертає n-те просте число.

PrimePi[x]повертає кількість простих чисел які не перевищують x.

N[k,n] – повертає число k із n знаками після коми.

Rationalize[z,n]- число z перетворюється в раціональне число. (у вигляді дробу).

f//N – обчислює вираз f в чисельному вигляді, з наближеним значенням .

%- повертає результат останньої операції

% - повертає результат передостанньої операції.

%n – повертає результат операції виконаної n операції назад.

FullSimplify[exp]- спрощення виразу exp.

TrifExpand[f]- перетворення тригонометричних виразів.

Expand[f] – розкриває дужки добутків і підносить до степені вираз. Виконує дії із спеціальними функціями. Виконує розкриття і розширення функцій, яке задає змінні у вигляді дійсних чи комплексних змінних.

Togather- призводить да спільного знаменника.

Collect[f,x] – переводить спільних членів функції за змінними x. Також можна використовувати Collect[f,{x1,x2,…}].

Simplify – спрощення виразу.

PowerExpand	Раскрывает все степени степеней и произведений
ComplexExpand	Раскрывает комплексные выражения, при этом все переменные подразумеваются вещественными числами

TrigReduce[f] – cghjoe'спрощує вирази, які містять тригонометричні функції.

TrigExpand[f] виконує розширення тригонометричних функцій.

TrigFactor[f] розбиває на множники тригонометричні функції.

TrigToExp[f] представляє тригонометричний вираз в експоненціальній формі.

Функції генерування випадкових чисел:

Random[] – випадкове число рівномірно розподілене на інтервалі [0,1].

Random[type,range] випадкове число вказаного типу, яке міститься у вказаному інтервалі.

SeedRandom[n] встановлює генератор, число n вик як початкове.

PoverExpand[f] – розкриває дужки і вертає в цілу додатню степінь вкладені вирази функції f.

FunctionExpand[f] – представляє спрощені вирази функції f, яке містить спеціальні функції.

Комплексні числа задаються у вигляді: z=Re[z]+I*Im[z], де I-комплексне число.

Re[z] – дійсна частина числа.

Im[z] – уявна частина числа.

Abs[z] – абсолютна величина z/

Arg[z]- аргумент z.

Conjugate[z]- комплексно спряжене до z.

f(x)/.x->a підставляє у вираз f(x) замість xзначення a.

f(x,y,..)/.{x->a, y->b,…} виконує підстановку у вираз f(x,y,..), замість x,y,… відповідні значення a,b,…

{f1(x,y,…), f2(x,y,…),…}/.{x->a, y->b,…} підстановка замість x,y,… відповідні a,b,… у дані функції.

У випадку f(x)/. x->{x0,x1,x2,…} -табулювання функції f з відповідними значеннями

Основними елементарними функціями називають такі функції.

Степенева функція .

Показникова функція

Логарифмічна функція

Тригонометричні функції

Обернені тригонометричні функції:

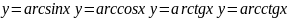
Гіперболічні функції:

Обернені гіперболічні функції: