2.5.1.Закон обучения Кохонена
Модификация весовых коэффициентов происходит в соответствии с законом
,
где
.
То есть весовые коэффициенты изменяются только у победившего нейрона.
Этот закон можно записать так:
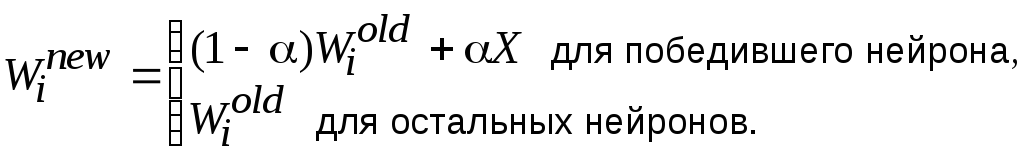
В
начале обучения выбирается
.
Затем значение
уменьшают.
Самоорганизующиеся структуры используются , в основном, для решения задач распознавания образов. Эти структуры классифицируют образы, представленные векторными величинами, в которых каждый компонент вектора соответствует элементу образа.
После обучения подача на вход сети вектора из данного класса будет приводить к выработке возбуждающего уровня в каждом выходном нейроне. Нейрон с максимальным возбуждением определяет класс. Так как обучение производится без указания целевого вектора, то нет возможности определить заранее, какой нейрон будет соответствовать данному классу входных векторов. Это планирование осуществляется путем тестирования после обучения. По мнению Кохонена, для получения хорошей статистической точности количество обучающих циклов должно быть примерно в 500 раз больше количества выходных нейронов.
Но
закон Кохонена в такой форме не позволяет
найти равновероятно распределенные
весовые векторы. Эта задача решается
следующим образом. Вводится понятие
времени
,
т.е. параметра, характеризующего
количество побед нейрона
в конкуренции,
,
затем вычисляется текущее значение
смещения
— это величина, с помощью которой частота
побед
-го
нейрона сравнивается с
.
Нейроны, которые побеждали часто, имеют
большое отрицательное смещение. Те,
которые побеждали редко — наоборот.
Нейроны, величина смещения которых
меньше некоторого порога
,
“изымаются” из конкуренции. Так получают
весовые векторы, распределенные в сети
в равновероятной конфигурации.
2.5.2.Закон обучения Гроссберга
ИНС, в основу функционирования которых заложена идея Гроссберга, считаются одними из самых продуманных с точки зрения топологии организации нейронных вычислений. Такие ИНС способны обучаться распознаванию образов различной степени сложности. Сеть относит входной образ к одному из классов в зависимости от того, на какой из известных сети образов он более всего похож. Если входной образ не соответствует ни одному из запомненных, то автоматически создается новый класс.
ИН
Гроссберга представлен на рис.2.4. Связи,
по которым передаются входные сигналы
,
имеют весовые коэффициенты
.
На вход нейрона подается также значение
желаемого выходного сигнала
,
а действительное значение выходного
сигнала обозначается
.
Основной
посылкой закона Гроссберга является
то, что передаточная функция нейронов
слоя Гроссберга неизвестна. Входной
сигнал
в определенные моменты времени становится
активным, т.е. его значение не равно
нулю. Тогда вес связи, по которой
передается этот сигнал, изменяется в
соответствии со следующим равенством:
(*)
Рис.2.4. ИН Гроссберга
Если
ось времени
преобразовать в ось времени
,
исключив из
те моменты времени, когда
,
то можно будет записать равенство (*) в
виде скалярного дифференциального
уравнения, называемого уравнением
махового колеса
,
решением которого является среднее
значение по времени произведения
за время, при котором
,
т.е.
.
Такое значение, по закону Гроссберга,
примет вес
-й
связи после долгого обучения.