3.2.2.Сети со встречным распространением ошибки

Сеть со встречным распространением ошибки аппроксимирует непрерывную функцию . Здесь описано подмножество таких сетей, требующее, чтобы функция имела свойство непрерывности.

Обучение сети состоит из трех этапов. Принимается, что вектор для обучения сети выбирают из в соответствии с некоторой фиксированной функцией плотности вероятности .

Сеть состоит из трех слоев: входного слоя нейронов, передающих входные сигналы , и нейронов, передающих значения корректных выходных сигналов ; среднего слоя (слоя Кохонена) нейронов, формирующих выходные сигналы ; выходного слоя (слоя Гроссберга) нейронов, формирующих выходные сигналы .

На первом этапе обучения сети после выбора определяется и оба значения вводятся в сеть. Обучение проходит по закону Кохонена.

Можно доказать, что средняя квадратическая ошибка сети может быть уменьшена до любого желаемого уровня с помощью выбора достаточно большого количества нейронов среднего слоя. То есть эта сеть более эффективна в смысле уменьшения средней квадратической ошибки, чем сеть с обратным распространением ошибки.

3.3.Стохастические сети. Машина Больцмана

Модель ИНС, называемая машиной Больцмана, разработана на основе работ Киркпатрика. Здесь проведена аналогия со статистической физикой: для частной системы вероятность ее пребывания в данном состоянии пропорциональна показателю Больцмана , где — энергия состояния,  — температура системы. Так как, с другой стороны, нейронный подход к задачам оптимизации сводится к поиску локального минимума, показатель Больцмана связывают с энергией сети Хопфилда, которая определена ранее, прежде чем улучшать сходимость вероятности к глобальному минимуму. Основная концепция функционирования машины Больцмана заключается в моделировании отжига в металлургии, при котором металлическое тело нагревают до температуры, близкой к точке плавления, и затем медленно охлаждают. При этом кристаллическая структура с дефектами разрушается в результате термического нагрева, а при охлаждении формируется новая. Суть этого процесса — в минимизации некоторой энергетической функции. Математическая основа метода основывается на использовании метода Монте-Карло для описания состояния сред, состоящих из множества взаимодействующих молекул. Общий процесс минимизации энергетической функции в системе разделен на ряд локальных процессов. Основная идея метода состоит в поочередной замене отдельной случайно выбранной в некоторый момент времени части системы и анализе результата этой замены.

Для детерминированных сетей существуют две модели функционирования — последовательная и параллельная. Для симметричной цифровой последовательной модели сети изменение энергии, связанное с изменением состояния нейрона, , при . Для машины Больцмана с синаптическими весами изменение состояния определяется случайным розыгрышем с вероятностями , пропорциональными показателю Больцмана . После нормализации получаются следующие вероятности переходов: 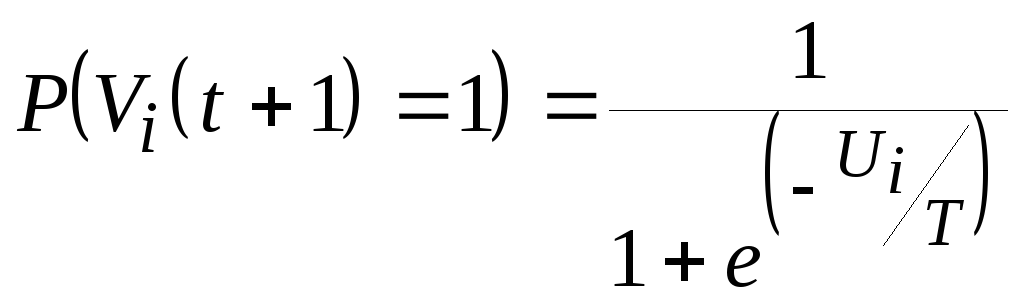и .

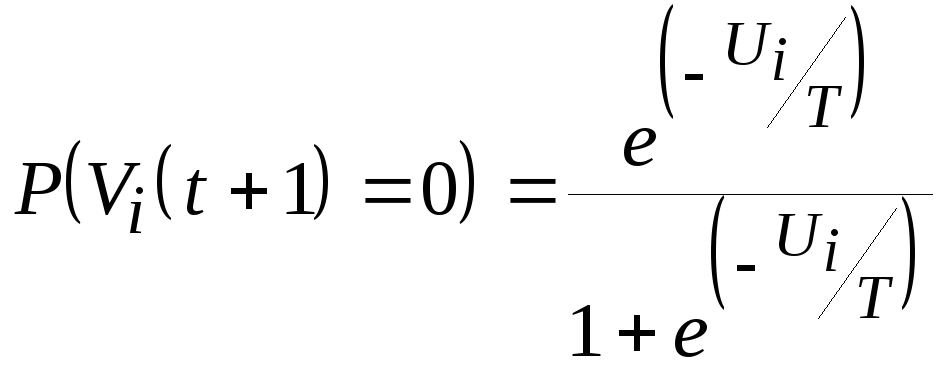Интересно заметить, что оценка среднего значения для нейрона прямо связана со значением выхода нейрона в аналоговой сети Хопфилда. Чтобы добиться сходимости остается выбрать убывающий закон для температуры . В начале сходимости для очень высоких температур каждый нейрон ведет себя квазислучайным образом: .

Впоследствии, так как температура понижается, именно внутреннее состояние определяет выход нейрона, а для температур, близких к нулю, случайный компонент исключается и сеть ведет себя как детерминированная сеть Хопфилда.

Алгоритм решения задачи оптимизации следующий:

Этап 1. Вычисление синаптических весов и по формуле энергии Ляпунова с оптимизируемой квадратичной формой.

Этап 2. Случайная инициализация выхода нейронов и задание .

Этап 3. Выбор нейрона и вычисление значения энергии, которое могло бы привести к изменению состояния выхода .

Этап 4. Согласованные изменения состояния с вероятностью по формуле, описанной выше.

Этап 5. Возвращение к этапу 3. После итераций уменьшение температуры .

Этап 6. Возвращение к этапу 3 до сходимости сети (для последовательных опытов, пока не будет достигнут результат).

Возможно применить более “нейронный” подход к этапам 3 и 4, переформулировав их таким образом:

Этап 3. Выделение некоторого нейрона и вычисление его внутреннего состояния .

Этап 4. Вычисление выхода нейрона , где с вероятностью, меняющейся по сигмоиде.

Последовательная машина Больцмана моделируется последовательностью однородных цепей Маркова длины . Для последовательной схемы машина Больцмана является цифровой сетью Хопфилда, которая обеспечивает сходимость к глобальному минимуму .

Параметрами, определяющими алгоритм, являются:

•  закон убывания температуры и начальная температура ;

•  длина цепи Маркова;

•  критерий завершения (число итераций), который обеспечивает сходимость.

Параллельная машина Больцмана характеризуется тем, что в ней все или часть нейронов на каждой итерации контролируют вероятность изменения ее состояния выхода.

Приняв алгоритм, представленный для последовательной машины, этапы 3 и 4 следует изменить: для , меняющегося от 1 до , нейрон вычисляет вероятность изменения своего состояния .

Возможные изменения состояния являются одновременными. Параметры алгоритма те же, что и для последовательной машины.

Таким образом, решение задач оптимизации машиной Больцмана основывается на тех же принципах, что и для детерминированной сети — каждая конфигурация машины связана с решением задачи.

Фактически, машина Больцмана — это сеть Хопфилда с дискретным временем, в которой передаточная функция нейрона изменена для использования процедуры моделирования отжига.

Передаточная функция ИН в машине Больцмана определяется так:

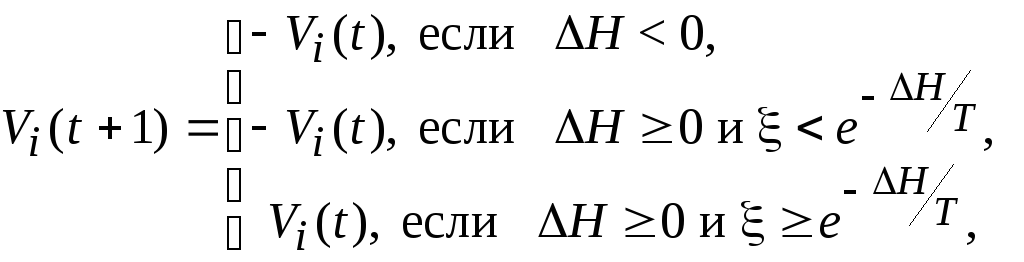
где 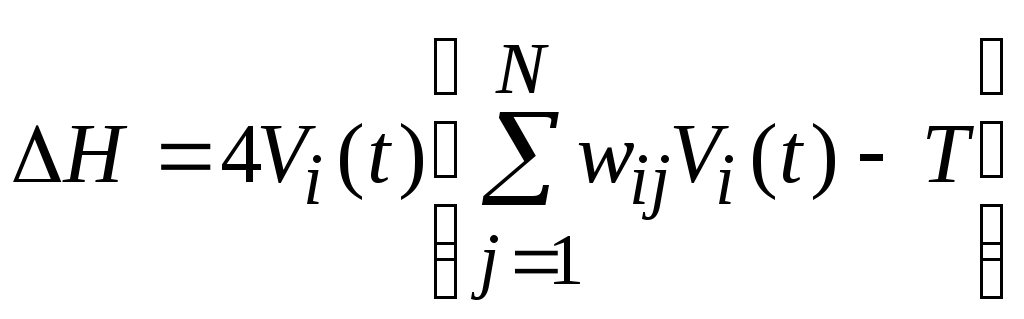; —температура; —случайное число, , выбирается с помощью функции плотности вероятности.

Практические условия асимптотического функционирования возникают редко, и машина Больцмана не гарантирует сходимости к глобальному минимуму, однако она улучшает скорость сходимости цифровых детерминированных сетей Хопфилда.

Если необходимо искать хорошее решение быстро, лучше использовать аналоговую сеть Хопфилда, а если можно искать наилучшее решение при любом времени сходимости, нужно использовать стохастическую сеть, для которой сходимость более медленная, а выбор параметров более трудный, чем для детерминированной сети.

Сети преобразования данных решают задачи, связанные с приближенной реализацией функций вида . Классическими примерами сетей, разработанных для решения таких задач, являются сети с обратным и встречным распространениями ошибки.