5. Метод Парето

Принцип Парето: смысл введенного понятия эффективного решения состоит в том, что оптимальное решение следует искать только среди элементов множества Парето - множества P(D). В противном случае всегда найдется точка x, оказывающаяся более предпочтительной независимо от расстановки приоритетов и относительно важности отдельных частных критериев.

Принцип Парето позволяет сузить класс возможных претендентов на окончательное решение и исключить из рассмотрения заведомо неконкурентноспособные варианты. А окончательный выбор осуществляется на основе дополнительной информации о предпочтении лица, принимающего решения.

Рассмотрим введенные понятия на примере.  

Пример 

F(x) ={3x₁-x₂ ; x₂}->max , т.е.  f₁(x)= 3x₁-x₂->max f₂(x)= x₂->max x₁≤2  x₂≤4  2x₁+x₂≤6 x_j≥0

С помощью графического метода найдем субоптимальные решения (см рис. 5.1). По критерию f₁ - это точка Е(2,0), f₁(Е)=6.

По критерию f₂ субоптимальные точки - это точки отрезка, соединяющего точки С(0,4) и В(1,4),], при этом f₂(С) = f₂(В)=4

 

Таблица 5.1 – Анализ точек множества D примера 1 на принадлежность множеству Парето

XD	f1(x)	f2(x)	Примечание	Свойство решения
A(2,2)	4	2	Не улучшаемые точки	P(D)
B(1,4)	-1	4	-“-	P(D)
G(1,5, 3)	1,5	3	-“-	P(D)
E(2,0)	6	0	-“-	P(D)
C(0,4)	-4	4	Улучшаемая по 1-му критерию	S(D) P(D)
K(0,0)	0	0	Одновременно улучшаемая по обоим критериям	P(D), S(D)
L(1,1)	2	1

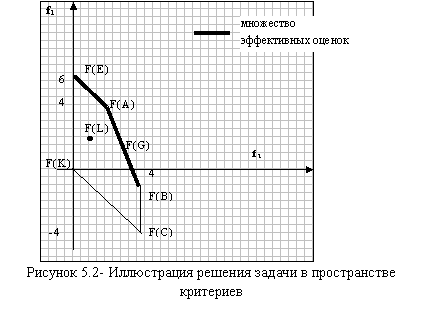
В таблице 5.1 приведены значения целевых функций f₁(x)= 3x₁-x₂  и f₂(x)= x₂ для всех точек, обозначенных на рис. 5.1. На основании этих данных построен рис. 5.2. Полученный многоугольникF(C) F(K) F(E) F(A) F(G) F(B)  является отображением многоугольника допустимых решений примера C K E A G B  в пространсте критериев.