Уравнение модели сарм

В модели САРМ простым образом определяется связь между риском и доходностью эффективных портфелей. Это наглядно представлено на рисунке ниже:

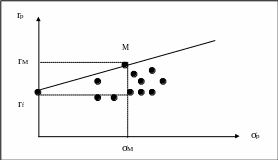
Точка М обозначает рыночный портфель, а rf представляет собой безрисковую ставку доходности. Эффективные портфели находятся вдоль прямой, пересекающей ось ординат в точке с коорди­натами (0, r) и проходящей через М, и образуются альтернативными комбинациями риска и доходности, получаемыми в результате сочетания рыночного портфеля с безрис­ковым заимствованием или кредитованием. Это линейное эффективное множество в САРМ известно под названием рыночная линия (Capital Market Line, CML). Все осталь­ные портфели, не использующие рыночный портфель в комбинации с безрисковым заимствованием или кредитованием, будут лежать ниже рыночной прямой, хотя неко­торые могут располагаться в непосредственной близости от нее.

Н аклон СМL равен разнице между ожидаемой доходностью рыночного портфеля и безрисковой бумаги, деленной на разницу их рисков. Так как СМL пересекает вертикальную ось в точке с координа­тами (0, r), то уравнение СМL имеет вид:

Состояние равновесия на рынке ценных бумаг может быть охарактеризовано дву­мя ключевыми величинами. Первая - это ордината точки пересечения СМL с верти­кальной осью (т.е. безрисковая ставка), которую часто называют наградой за ожидание. Вторая — это наклон СМL, который называют наградой за единицу принятого риска.

Источники

1. Шарп У., Александер Г., Бэйли Дж. «Инвестиции». – М.: «ИНФРА-М», 2001 г.

2. «Рынок ценных бумаг» - под ред. В.А. Галанова, А.И. Басова. – М.: «Финансы и статистика», 1999 г.

3. «Справочник финансиста предприятия» - 2-е изд., доп. и перераб. – М.: «ИНФРА-М», 1999 г.

Контрольные вопросы и задачи

1. Ниже приводится список некоторого количества портфелей с их ожидаемыми доходностями, стандартными отклонениями и уровнем полезности (измеряемым в услов­ных единицах). Исходя из этой информации необходимо построить график кривых безразличия инвестора.

Портфель	Ожидаемая доходность, %	Стандартное отклонение, %	Полезность
1	5	0	10
2	6	10	10
3	9	20	10
4	14	30	10
5	10	0	20
6	11	10	20
7	14	20	20
8	19	30	20
9	15	0	30
10	16	10	30
11	19	20	30
12	24	30	30

2. Почему делается предположение, что кривые безразличия наклонны и направлены вверх и вправо?

3. Что говорит набор выпуклых кривых безразличия об оценке инвестором соотно­шения риска и доходности для различных значений риска?

4. Почему предполагается, что типичный инвестор предпочитает портфель, располо­женный на кривой безразличия выше и левее?

5. Объясните, почему кривые безразличия инвестора не могут пересекаться?

6. Почему кривые безразличия инвестора, избегающего риска в большей степени, имеют более крутой наклон, чем кривые безразличия инвестора, избегающего ри­ска в меньшей степени?

7. Имея следующую информацию об акциях, входящих в портфель, вычислите для каждой акции ожидаемую доходность. Затем, используя эти индивидуальные ожидаемые доходности ценных бумаг, вычислите ожидаемую доходность порт­феля.

Акция	Начальная стоимость инвестиции, руб.	Ожидаемая стоимость инвестиции в конце периода, руб.	Доля в начальной рыночной стоимости портфеля, %
A	500	700	19,2
B	200	300	7,7
C	1000	1000	38,5
D	900	1500	34,6

8. И ковариация, и коэффициент корреляции измеряют степень взаимосвязанности доходностей двух ценных бумаг. Какая зависимость существует между этими двумя статистическими мерами? Почему коэффициент корреляции является более удоб­ной мерой?

9. Приведите пример двух обыкновенных акций, для которых, как вы ожидаете, кор­реляция будет относительно низкой. Затем приведите пример двух обыкновенных акций, которые будут иметь относительно высокую корреляцию.

10. Укажите ключевые предположения, лежащие в основе САРМ.

11. Многие из исходных предположений модели САРМ не вполне соответствуют реаль­ности. Следует ли отсюда, что и выводы из модели неверны? Объясните.

12. Нарисуйте прямую рыночных активов, если ожидаемая доходность рыночного порт­феля составляет 12%, его стандартное отклонение — 20%, а безрисковая процент­ная ставка - 6%.

13. Инвестор располагает ценными бумагами А, Б, В со следующими показателями β= 2; 1,3; -0,5 соответственно. Определить на сколько изменится доходность каждой ценной бумаги, если среднерыночная доходность увеличится на 10%.

14. Определить, является ли данный портфель сформированным эффективно:

Наименование ценной бумаги	Стоимость на начало периода	Стоимость на конец периода	Дивиденды
А	5 000	6 000	500
В	4 000	7 000	400
С	2 000	3 000	100
Д	10 000	7 000	1 000

β портфеля = 1,3;

Доходность безрисковых вложений - 10 %;

Среднерыночная доходность – 15 %.

14