Министерство сельского хозяйства РФ

ФГБОУ ВПО «Великолукская государственная сельскохозяйственная академия »

Кафедра информатики, информационных технологий и систем управления.

КУРСОВАЯ РАБОТА

по дисциплине «Информатика»

«Автоматизация инженерных задач»

Выполнил: студент 1 курса заочного отделения инженерного факультета

Степанов В.Ю.

Зачет. Книж №11778

Проверил: Зав. каф.

Чертова М.Н.

Великие Луки - 2012

С одержание

Введение 3

2.Описание численного метода решения СЛАУ 4

2.1.Общяя характеристика методов 4

2.2.Метод Крамера в решении СЛАУ 7

3.Прикладное ПО применяемое для решения СЛАУ 9

4.Практическое применение MS Excel 18

4.1.Постановка задачи 18

4.2.2.Решение СЛАУ с помощью MS Excel 20

Заключение 22

СПИСОК ЛИТЕРАТУРЫ 24

Введение

Многие инженерные задачи требуют решения системы линейных алгебраических уравнений (СЛАУ). С появлением ВТ в математике активно развивается направление, связанное с реализацией методов решения таких задач с помощью ЭВМ, которое называют вычислительной математикой. Для решения инженерных задач на ЭВМ с использованием численных методов чаще всего применяются готовые программы обеспечения, например, MathCAD, MS Excel и другие.

Линейные системы имеют в вычислениях очень большое зна­чение, так как к ним сводится приближенное решение широкого круга вычислительных задач вообще и инженерных задач в ча­стности. Теория решения линейных систем достаточно хорошо разработана и во многих частях доведена до совершенства. Име­ется большое число разнообразных программных средств для ре­шения самых различных систем уравнений, в том числе плохо обусловленных, блочных, с разреженными матрицами и т.д.

Целью курсовой работы являются приобретение навыков автоматизации инженерных расчетов в табличном процессоре MS Excel.

Задачами курсовой работы являются:

1. Решить систему алгебраических уравнения методом Крамера традиционным способом.

2. Использовать MS Excel в решении системы алгебраических уравнений.

2.Описание численного метода решения слау

2.1.Общяя характеристика методов

Методы решения линейных систем уравнений обычно разде­ляют на две большие группы. К первой группе относят методы, которые принято называть точными. Они позволяют для любых систем в принципе найти точные значения неизвестных после ко­нечного числа арифметических операций, каждая из которых вы­полняется точно.

Ко второй группе относят все методы, не являющиеся точны­ми. Их обычно называют приближенными итерационными, ре­шения в них получают в результате бесконечного процесса при­ближений. Особое место среди них (нередко их даже выделяют в отдельную группу) занимают вероятностные методы, в основу которых положены соображения, взятые из теории вероятностей. Такие методы полезны лишь в случаях очень высокой размерно­сти систем и более упоминаться, не будут.

В общем виде линейная система уравнений записывается сле­дующим образом:

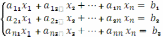
или чаще — в матричном виде: ах-В, где а — квадратная мат­рица размером n x n, B и x — векторы размером n (n — размер­ность системы).

Точные методы

Точные методы обычно рассматриваются в курсах линейной алгебры, поэтому здесь упомянем коротко основные особенности самых распространенных методов для сопоставления с итераци­онными, которые обычно изучаются в курсах прикладной мате­матики.

Метод Гаусса сводится к двум этапам. На первом осущест­вляется приведение исходной системы уравнений с помощью преобразований к эквивалентной системе с верхней треугольной матрицей (т.е. приведение системы к треугольному виду). Преоб­разования сводятся к умножению всех членов уравнения на по­стоянное число, сложению уравнений, выражению отдельных пе­ременных через другие и т.п. Это прямой ход. На втором этапе, т.е. в обратном ходе (снизу вверх), находятся последовательно все переменные системы. В отдельных случаях, в частности при умножении всех членов уравнения на очень большое число (или при делении на очень маленькое), появляются большие вычисли­тельные ошибки, которые обусловливают значительные погреш­ности результатов решения.

Более практичным является метод оптимального исключе­ния, представляющий собой видоизменение метода Гаусса и требующий меньше памяти для решения. Здесь обратный ход соединен с прямым ходом за счет исключения всех уже выражен­ных переменных из вышестоящих уравнений.

Упомянем также метод Крамера (с использованием опреде­лителей), который требует очень больших вычислений уже при прямом решении систем из пяти—десяти уравнений, приведения матрицы А к форме произведения двух треугольных матриц, что позволяет свести решение заданной системы к последовательно­му решению двух систем с треугольными матрицами, что являет­ся задачей более простой. Поэтому вычисления определителей для матриц высокого порядка осуществляются обычно приближенными методами, и метод Крамера перестает быть в полном смысле точным.

Во всех методах этой группы может появляться накапливаю­щаяся вычислительная ошибка (не алгоритмическая!). Для ее контроля (а не для управления ею!) применяют специальные приемы. Например, в методе Гаусса к каждой строке добавляют еще один член, который равен сумме всех коэффициентов строки. С этим членом делают те же операции, что и с коэффициентами уравнения. На каждом шаге проверяют равенство суммы коэффи­циентов и “контрольного" добавленного члена: разница говорит о появлении накопившейся вычислительной погрешности. Можно оценивать не только абсолютную, но и относительную ошибку в равенстве суммы коэффициентов и “контрольного” добавленного члена. Таким образом, точные методы могут давать результат с погрешностью, которой трудно управлять и которая в ряде случа­ев может оказаться значительной, например, при высоких поряд­ках системы.

В заключение отметим, что системы с плохо обусловленными матрицами коэффициентов нецелесообразно решать указанными методами вследствие возможности появления очень больших ошибок.