
- •Часть 2
- •Часть 2
- •Задания к контрольной работе 3
- •Методические указания к контрольной работе 3
- •2. Предельный признак сравнения.
- •5. Интегральный признак Коши.
- •1) , 2) (Последовательность убывает), тогда знакочередующийся ряд (4) сходится.
- •Однородное уравнение.
- •Линейным уравнением первого порядка называется уравнение вида , (11)
- •5. Уравнением Бернулли называют уравнение следующего вида
- •Уравнение со специальной правой частью второго типа.
- •Метод вариации произвольных постоянных.
- •Задания к контрольной работе 4
- •Методические указания к контрольной работе 4
- •Число размещений .
- •Число перестановок .
- •Число сочетаний .
- •Формула полной вероятности.
- •Формула Байеса.
Формула полной вероятности.
Пусть
события
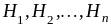 образуют полную группу попарно не
образуют полную группу попарно не
совместных
событий (гипотез), то есть
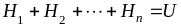 и
и
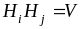 ,
если
.
Тогда вероятность событий можно вычислять
по формуле
,
если
.
Тогда вероятность событий можно вычислять
по формуле
 ,
,
которая называется формулой полной вероятности.
Пример. Из 28 костей домино поочерёдно вытащили наугад 2 кости. Найти вероятность того, что вторую кость домино можно приставить к первой согласно правилам игры.
Чтобы
внести определённость рассмотрим
возможные гипотезы
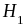 =
{первая извлечённая кость является
дублем},
=
{первая извлечённая кость является
дублем},
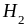 =
{первая извлечённая кость не является
дублем}. Имеем
=
{первая извлечённая кость не является
дублем}. Имеем
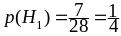 ,
,
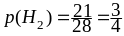 .
Найдём условные вероятности:
.
Найдём условные вероятности:
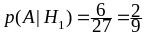 ,
,
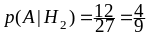 .
Из формулы полной вероятности находим,
что
.
Из формулы полной вероятности находим,
что
 .
.
Формула Байеса.
Эта
формула используется для пересчёта
вероятностей гипотез
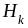 ,
,
(k = 1, 2, … , n), после того, как произошло некоторое событие . Пусть, как в предыдущем пункте, события образуют полную группу попарно несовместных событий (гипотез). Тогда справедливо равенство (формула Байеса)
 .
.
Пример. Имеется 3 урны, в которых находятся 1 белый и 2 чёрных, 2 белых и 2 чёрных, 3 белых и 2 чёрных шара соответственно. Из первой урны переложили во вторую 1 шар, затем из второй урны переложили в третью 1 шар, после чего из третьей урны извлекли наугад один шар. Найти вероятность того, что из второй урны в третью переложили белый шар, если шар, извлечённый из третьей урны, оказался чёрным.
Введём
две пары гипотез
=
{из первой урны во вторую переложили
белый шар},
=
{из первой урны во вторую переложили
чёрный шар};
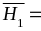 {из
второй урны в третью переложили белый
шар},
{из
второй урны в третью переложили белый
шар},
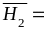 {из
второй урны в третью переложили чёрный
шар}. Введём также событие
{из
второй урны в третью переложили чёрный
шар}. Введём также событие
= {из третьей урны извлекли чёрный
шар}. Вероятности гипотез
 ,
,
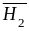 найдём по формуле полной вероятности.
Имеем
найдём по формуле полной вероятности.
Имеем
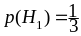 ,
,
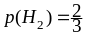 ,
,
 ,
,
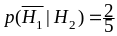 .
Следовательно,
.
Следовательно,
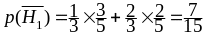 .
Аналогично,
.
Аналогично,
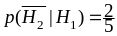 ,
,
 ,
а
,
а
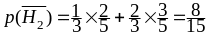 .
Найдём теперь условные вероятности
события
при условии, что собы–
.
Найдём теперь условные вероятности
события
при условии, что собы–
тия
,
произошли:
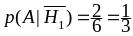 ,
,
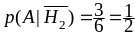 .
Следовательно, искомая вероятность
.
Следовательно, искомая вероятность
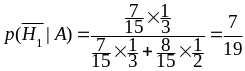 .
.
Задание 4. Повторные испытания. Формула Бернулли.
Пусть некоторый
случа йный эксперимент (испытание)
повторяется n раз в
одинаковых условиях, а вероятность
p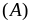 осуществления
события
в каждом испытании равна
осуществления
события
в каждом испытании равна и не зависит от испытания. Число
осуществлений события
в n независимых
испытаниях называют частотой события
и
обозначают
и не зависит от испытания. Число
осуществлений события
в n независимых
испытаниях называют частотой события
и
обозначают
 .
Обозначим
.
Обозначим
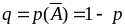 ,
,
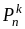 – вероятность того, что в n
испытаниях событие
произойдёт ровно k
раз, то есть
– вероятность того, что в n
испытаниях событие
произойдёт ровно k
раз, то есть
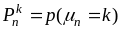 .
Справедливо равенство, которое называют
формулой Бернулли
.
Справедливо равенство, которое называют
формулой Бернулли
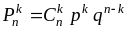 .
(21)
.
(21)
Пример. Две игральных кости бросают 5 раз. Найти вероятность того, что ровно 3 раза выпадет хотя бы одна шестёрка.
В
этом случае событие
= {выпала хотя бы 1 шестёрка} и
вероятность этого события в каждом из
5 испытаний
 1–
1–
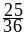 =
=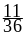 .
Из (21), для n = 5, k
= 3, получаем
.
Из (21), для n = 5, k
= 3, получаем
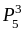 =
=
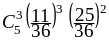 =
0,138 (результат округлён до тысячных).
=
0,138 (результат округлён до тысячных).
Формула Бернулли используется для вычисления вероятностей следующих событий

Так
как события
 ,
,
 ,
несовместны, а событие
,
несовместны, а событие
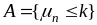 =
=
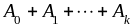 ,
то из формулы Бернулли следует, что
,
то из формулы Бернулли следует, что
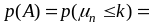
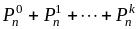 .
Аналогично получим, что
.
Аналогично получим, что

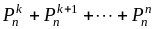 ,
,
 .
.
Пример. Найти вероятность того, что шестизначный номер телефона содержит не менее двух и не более пяти девяток (считать, что любая цифра номера может принимать любое значение от 0 до 9).
В
этом случае каждая цифра номера является
случайным испытанием
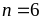 ,
а событие
= {цифра номера является 9}. Из сказанного
выше следует, что
,
а событие
= {цифра номера является 9}. Из сказанного
выше следует, что
 ,
,

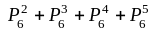 =
=
 +
+
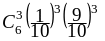 +
+
 +
+
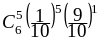 =
=
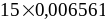 +
20
+
20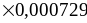 +
15
+
15 0,114264.
0,114264.
Локальная теорема Лапласа
При
больших значениях n
формула (21) не удобна в применении, так
как
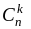 может
быть очень большим числом. В этом случае
для вычисления
пользуются
локальной теоремой Лапласа: если
может
быть очень большим числом. В этом случае
для вычисления
пользуются
локальной теоремой Лапласа: если

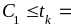

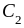 ,
,
 ,
тогда
,
тогда
 .
.
Иначе говоря, при больших значениях числа испытаний можно пользоваться приближённым равенством
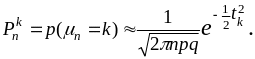 (22)
(22)
Замечание.
Чаще всего формулой (22) пользуются при
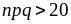 ,
когда n достаточно
велико, а p и q
не очень близки к нулю.
,
когда n достаточно
велико, а p и q
не очень близки к нулю.
Пример. Две игральные кости подбросили 100 раз. Найти вероятность того, что ровно 55 раз сумма выпавших цифр будет делиться на 2.
Обозначим
= {сумма выпавших очков при одном бросании
делится на 2}. Событие A
осуществляется в тех случаях, когда на
обоих кубиках выпадают нечётные либо
чётные числа. На каждом кубике 3 чётных
и три нечётных числа. Следовательно,
событие A осуществляется
в
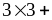
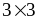 =18
из 36 случаях и вероятность p
=18
из 36 случаях и вероятность p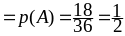 ,
,
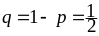 .
Имеем
.
Имеем
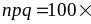
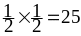 ,
,
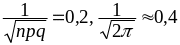 ,
,
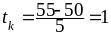 .
Следовательно,
.
Следовательно,
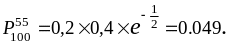
Интегральная теорема Лапласа
При
больших n для вычисления
вероятности
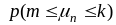 того, что в n независимых
испытаниях событие A
произойдёт не менее m
и не более k раз
используется приближённая формула
того, что в n независимых
испытаниях событие A
произойдёт не менее m
и не более k раз
используется приближённая формула
 (23)
(23)
где
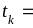
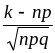 ,
,

 ,
,
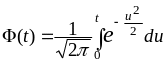 – функция Лапласа. Значения функции
Лапласа для 0
– функция Лапласа. Значения функции
Лапласа для 0
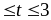 приводятся в специальных таблицах в
учебниках по теории вероятности и
математической статистике (в конце
книги). Для отрицательных значений
аргумента
приводятся в специальных таблицах в
учебниках по теории вероятности и
математической статистике (в конце
книги). Для отрицательных значений
аргумента
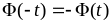 ,
так как функция Лапласа является
нечётной,
,
так как функция Лапласа является
нечётной,
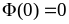 ,
а для значений аргумента
,
а для значений аргумента
 полагают приближённо
полагают приближённо
 .
.

Пример.
При передаче сообщения телеграфом
вероятность искажения одного знака
p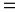 0,1.
Найти вероятность того, что в сообщении
из 900 знаков будет искажено а) не мене
80 и не более 100 знаков; б) не более 90
знаков.
0,1.
Найти вероятность того, что в сообщении
из 900 знаков будет искажено а) не мене
80 и не более 100 знаков; б) не более 90
знаков.
В
нашем примере n =
900,
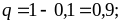
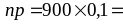

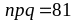 .
В случае а)
.
В случае а)
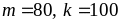 ,
и находим
,
и находим
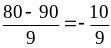 ,
,
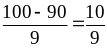 .
Следовательно,
.
Следовательно, =
= =
=
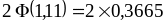 =
0.733. В случае б)
=
0.733. В случае б)
 ,
,
 ,
,
 .
Следовательно,
.
Следовательно,
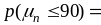
 .
.
Задание 5. Случайную величину, множество возможных значений которой (это действительные числа) конечно или счётно, называют дискретной случайной величиной, кратко ДСВ.
ДСВ
считается
заданной, если известны все её возможные
значения
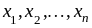 и вероятности
и вероятности
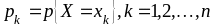 ,
с которыми случайная величина принимает
эти значения. В таком случае говорят,
что задан закон распределения этой
случайной величины. Вероятности
,
с которыми случайная величина принимает
эти значения. В таком случае говорят,
что задан закон распределения этой
случайной величины. Вероятности
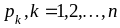 удовлетворяют условию нормировки
удовлетворяют условию нормировки
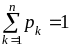 .
Рассмотрим пример выполнения задания
5.
.
Рассмотрим пример выполнения задания
5.
Пример.
В урне находится 15 лотерейных билетов,
5 из которых являются выигрышными. Из
урны извлекли наугад 3 билета. Пусть ДСВ
–
число извлечённых выигрышных билетов.
Составить закон распределения
,
вычислить математическое ожидание,
дисперсию
и
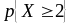 .
.
Возможными
значениями рассматриваемой случайной
величины являются числа 0,1,2,3. Найдём
вероятности этих возможных значений:
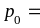
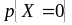 =
=
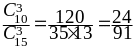 ,
,
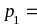
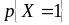 =
=
 ,
,
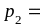
 =
= ,
,
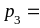
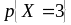 =
=
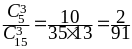 .
Проверим выполнение условия нормировки:
.
Проверим выполнение условия нормировки:
 +
+
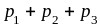 =
=
 +
+
 +
+
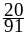 +
+
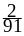 = 1. Математическое ожидание
= 1. Математическое ожидание
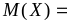
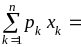
 +
+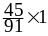 +
+
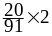 +
+
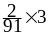 =
1, дисперсия
=
1, дисперсия
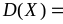
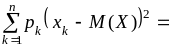
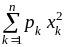 –
–
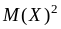 =
+
+
=
+
+
 +
+
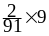 – 1 =
– 1 =
 ,
вероятность
=
,
вероятность
=
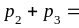 +
=
+
=
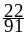 .
.
Задание
6. Пусть
![]() –
случайная величина (кратко СВ). Функцией
распределения вероятностей СВ
называют функцию
–
случайная величина (кратко СВ). Функцией
распределения вероятностей СВ
называют функцию
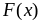 ,
которая определяется равенством
,
которая определяется равенством
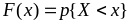 для любого действительного числа x.
для любого действительного числа x.
Под непрерывной случайной величиной (кратко НСВ) понимают такую случайную величину, множество возможных значений которой заполняют целый промежуток, а функция распределения вероятностей является непрерывной функцией. Из определения функции выводятся следующие основные её свойства:
 для любых действительных значений x;
для любых действительных значений x;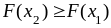 ,
если
,
если
 ,
то есть функция
возрастает;
,
то есть функция
возрастает;непрерывна слева, то есть
 (в
случае, если X является
непрерывной СВ, то
непрерывна);
(в
случае, если X является
непрерывной СВ, то
непрерывна);
 ;
;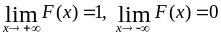 .
.
Для непрерывной случайной величины вводится ещё функция плот–
ности
распределения вероятностей
 ,
которая определяется равенством
,
которая определяется равенством
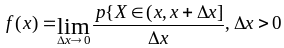 .
.
Из определения плотности распределения вытекают её основные свойства:
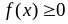 для любых x;
для любых x;условие нормировки
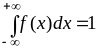 ;
;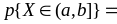
 ;
;из определения и свойства 4) устанавливается связь
между
плотностью распределения и функцией
распределения вероятностей, а именно
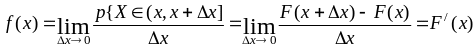 в точках дифференцируемости
(то
есть
является
первообразной для
);
в точках дифференцируемости
(то
есть
является
первообразной для
);
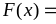
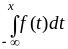 .
.
Пример.
Найти неизвестные параметры a,
b, математическое
ожидание M(X),
дисперсию
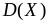 случайной величины X
и вероятность того, что
случайной величины X
и вероятность того, что
 ,
если функция распределения вероятностей
непрерывной случайной величины X
задана следующими равенствами
,
если функция распределения вероятностей
непрерывной случайной величины X
задана следующими равенствами
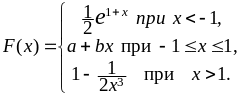
Параметры
a, b
определим из непрерывности функции
.
Из непрерывности функции
в точке
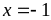 следует, что левосторонний предел
следует, что левосторонний предел
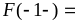
 равен правостороннему пределу
равен правостороннему пределу

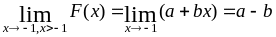 ,
а значит справедливо равенство
,
а значит справедливо равенство
 .
Аналогично, из непрерывности
в точке
.
Аналогично, из непрерывности
в точке
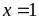 ,
приравнивая односторонние пределы
функции
в этой точке, получим второе уравнение
,
приравнивая односторонние пределы
функции
в этой точке, получим второе уравнение
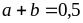 .
Следовательно, a и b
удовлетворяют линейной системе
.
Следовательно, a и b
удовлетворяют линейной системе
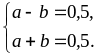 Решив полученную систему, находим a
= 0,5, а
Решив полученную систему, находим a
= 0,5, а
b = 0. Следовательно, с учётом найденных значений a и b, получаем
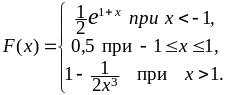
Из
свойства 4) находим
=
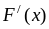 =
=
Математическое
ожидание непрерывной случайной величины
X найдём из равенства
 =
=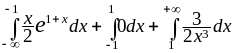 = (первый интеграл интегрируем по частям,
второй интеграл равен 0, а третий интеграл
является табличным) =
= (первый интеграл интегрируем по частям,
второй интеграл равен 0, а третий интеграл
является табличным) =
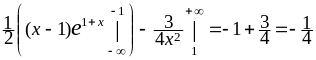 ,
так как
,
так как

 и
и

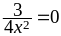 .
.
Для
вычисления дисперсии X
воспользуемся формулой
![]()
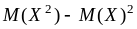 ,
из которой получаем
,
из которой получаем
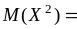
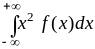 =
(с учётом функции плотности распределения
вероятностей
)
=
=
(с учётом функции плотности распределения
вероятностей
)
=
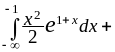
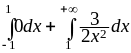 = (интегрируем по частям первый интеграл)
=
= (интегрируем по частям первый интеграл)
=
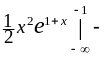
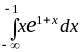 –
–
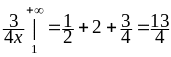 ,
так как
,
так как
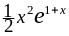 =
0. Следовательно, D(X)
=
=
0. Следовательно, D(X)
=
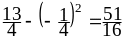 .
.
Вероятность
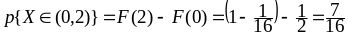 .
.
Пример.
Найти неизвестный параметр a,
математическое ожидание M(X),
дисперсию
,
функцию распределения
непрерывной случайной величины X
и вероятность того, что
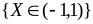 ,
если её плотность распределения
вероятностей
задана равенством
,
если её плотность распределения
вероятностей
задана равенством
 .
.
Из
условия нормировки имеем
 =
2a = 1. Следовательно,
=
2a = 1. Следовательно,
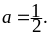
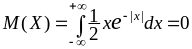 (интеграл
от нечётной функции
(интеграл
от нечётной функции
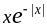 по симметричному промежутку
по симметричному промежутку
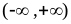 ).
).
Так как
 =
0, то D(X)
=
=
0, то D(X)
=
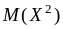 =
=
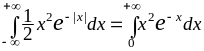 =
(интегрируем по частям) =
=
(интегрируем по частям) =
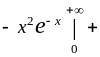
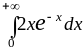 =
=
=
=
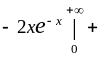
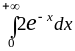 =
=
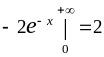 .
.
Найдём функцию
распределения вероятностей F(x)
=
.
Если
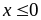 ,
тогда
,
тогда
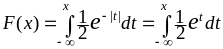 =
=
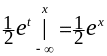 .
Если
.
Если
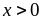 ,
то, по свойству аддитивности интеграла,
имеем F(x)
=
,
то, по свойству аддитивности интеграла,
имеем F(x)
=
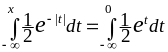 +
+ =
=
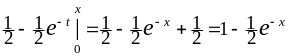 .
Следовательно, функция распределения
.
Следовательно, функция распределения
 Из свойства 4) функции распределения
находим
Из свойства 4) функции распределения
находим
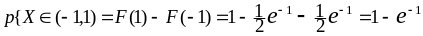 .
.
Задание 7. Пусть известны законы распределения двух ДСВ X,Y:
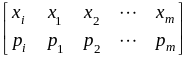 ,
,
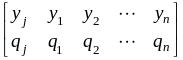 .
.
Определение.
Пусть
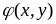 –
функция двух переменных. Функцией
–
функция двух переменных. Функцией
Z
=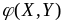 ДСВ X и Y
называется такая дискретная случайная
величина Z, возможными
значениями которой являются числа
ДСВ X и Y
называется такая дискретная случайная
величина Z, возможными
значениями которой являются числа
 ,
а вероятности
,
а вероятности
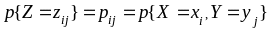 для всех
для всех
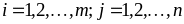 .
.
Вероятности
 характеризуют совместное распределение
случайных величин X,Y.
Перечислим основные свойства этих
вероятностей:
характеризуют совместное распределение
случайных величин X,Y.
Перечислим основные свойства этих
вероятностей:
условие нормировки
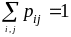 ;
;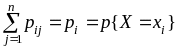 ;
3)
;
3)
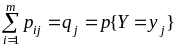 .
.
Определение.
ДСВ X, Y
называются независимыми, если для всех
выполняются равенства
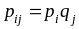 .
.
Для определения степени зависимости случайных величин X,Y
используется
коэффициент корреляции
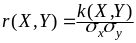 ,
где
,
где
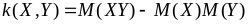 –
корреляционный момент, а
–
корреляционный момент, а
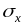 =
=
 ,
,
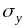 =
=
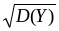 –
средне квадратичные отклонения СВ X,Y.
Известно, что
–
средне квадратичные отклонения СВ X,Y.
Известно, что
 и
и
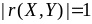 в случае линейной зависимости между
случайными величинами X
и Y.
в случае линейной зависимости между
случайными величинами X
и Y.
Пример.
Найти законы распределения случайных
величин X, Y,
X + Y,
XY, математические
ожидания и дисперсии случайных величин
X, Y,
X + Y,
XY и коэффициент
корреляции
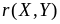 ,
если даны возможные значения СВ X,
Y и матрица вероятностей
:
,
если даны возможные значения СВ X,
Y и матрица вероятностей
:
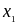 =
2,
=
2,
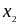 =
– 1,
=
– 1,
 =
–3;
=
–3;
 =
3,
=
3,
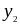 =
– 2,
=
– 2,
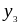 =
1,
=
1,
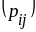 =
= .
.
Для нахождения
вероятностей
 воспользуемся
свойством 2):
воспользуемся
свойством 2):
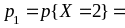 0,1
+ 0,1 + 0,1 = 0,3;
0,1
+ 0,1 + 0,1 = 0,3;
 0,1 + 0,15 + 0,15 = 0,4;
0,1 + 0,15 + 0,15 = 0,4;
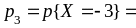 0,17 + 0,03 + 0,1 = 0,3. Следовательно, закон
распределения ДСВ X
имеет вид
0,17 + 0,03 + 0,1 = 0,3. Следовательно, закон
распределения ДСВ X
имеет вид
 .
Для нахождения вероятностей
.
Для нахождения вероятностей
 воспользуемся
свойством 3):
воспользуемся
свойством 3):
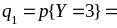 0,1
+ 0,1 + 0,17 = 0,37;
0,1
+ 0,1 + 0,17 = 0,37;
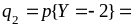 0,1
+ 0,15 + 0,03 = 0,28;
0,1
+ 0,15 + 0,03 = 0,28;
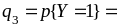 0.1+
0,15 + 0.1 = 0,35. Следовательно, закон
распределения ДСВ Y
имеет
0.1+
0,15 + 0.1 = 0,35. Следовательно, закон
распределения ДСВ Y
имеет
вид
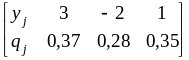 .
Возможные значения
.
Возможные значения
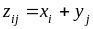 случайной
случайной
величины
Z = X
+ Y запишем в виде
матрицы
 .
Сложив соответствующие вероятности
0,1 + 0,15 + 0,17 = 0,42 для повторяющегося
возможного значения 0 случайной величины
Z, получим закон распределения
ДСВ Z = X
+ Y:
.
Сложив соответствующие вероятности
0,1 + 0,15 + 0,17 = 0,42 для повторяющегося
возможного значения 0 случайной величины
Z, получим закон распределения
ДСВ Z = X
+ Y:
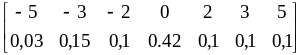 .
Найдём сначала в виде матрицы возможные
значения
.
Найдём сначала в виде матрицы возможные
значения
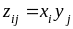 случайной величины Z =
X Y:
случайной величины Z =
X Y:
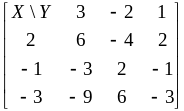 .
Сложив соответствующие вероятности
0,1 + 0,1 = 0,2; 0,1 + 0,15 = 0,25; 0,1 + 0,03 = 0,13 для
повторяющихся возможных значений –3;
2; 6 случайной величины Z,
получим закон распределения ДСВ Z
= X Y:
.
Сложив соответствующие вероятности
0,1 + 0,1 = 0,2; 0,1 + 0,15 = 0,25; 0,1 + 0,03 = 0,13 для
повторяющихся возможных значений –3;
2; 6 случайной величины Z,
получим закон распределения ДСВ Z
= X Y:
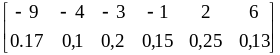 .
.
Математические
ожидания
 ;
;
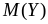 =
=
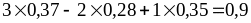 .
По свойству математического ожидания
имеем
.
По свойству математического ожидания
имеем
 =
– 0,7 + 0,9 = 0,2;
=
– 0,7 + 0,9 = 0,2;
 =
=
 .
.
Дисперсии
 =
=
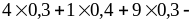 0,49 = 4,3 – 0,49 = 3,81;
0,49 = 4,3 – 0,49 = 3,81;

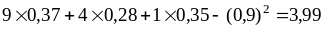 ;
;
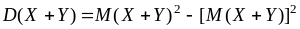 =
=
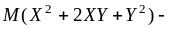
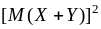 =
+ 2
+
=
+ 2
+
 –
=
4,3 + 2
–
=
4,3 + 2 =
6,26;
=
6,26;
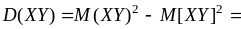

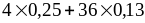 –
(–1,4)
–
(–1,4) =
4,68 – 1,96 = 2,72.
=
4,68 – 1,96 = 2,72.
Вычислим
теперь коэффициент корреляции
:
корреляционный момент
=
– 1,4 – (–0,7)
0,9
= – 0,77;
=
=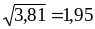 ;
=
=
;
=
= ;
=
;
=
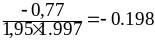 .
.
ЛИТЕРАТУРА
Данко, П.Е. Высшая математика в упражнениях и задачах. Т.1, Т.2/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высшая школа, 2003.– 460с.
Матвеев, Н.М. Методы интегрирования обыкновенных дифференциальных уравнений: Учебное пособие. – СПб.: Издательство «Лань», 2003.–832с.
Пискунов, Н.С. Дифференциальное и интегральное исчисления: Учеб. пособие для вузов. В 2 т.Т.1. и Т.2. – М.: Интеграл-Пресс, 2002.- 415 с. и 544с.
Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления: учебник в 3-х т. / Г. М. Фихтенгольц. - 9-е изд., стер. – СПб.; М.; Краснодар: Лань, 2009.–608,800, 672с.
ОГЛАВЛЕНИЕ
Введение...……………………………………………………………….3
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ 3…………………..…………….4
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ 3………10
Криволинейные интегралы…………………………………………..10
Двойной интеграл……………………………………………………..12
Тройной интеграл……………………………………………………..15
Поверхностные интегралы……………………………………………17
Формула Гаусса–Остроградского…………………………………...22
Теорема Стокса………………………………………………………....23
Потенциал векторного поля………………………………………….24
Числовые ряды, простейшие свойства рядов……………………….25
Признаки сходимости положительных рядов………………………27
Знакопеременные ряды………………………………………………...31
Степенные ряды, ряды Тейлора………………………………………33
Ряды Фурье…………………………………………………………….35
Дифференциальные уравнения первого и второго порядков……..40
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ 4…………………..……………50
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ 4………57
Преобразование Лапласа и его свойства……………………………57
Решение дифференциальных уравнений и систем с помощью
преобразования Лапласа……………………………………………..59
Формула классической вероятности…………………………………61
Условная вероятность, независимые события…………………….…63
Число размещений, перестановок и сочетаний………………….….65
Формула полной вероятности и формула Байеса………………….66
Повторные испытания, формула Бернулли…………………………68
Локальная и интегральная теоремы Лапласа……………………….69
Дискретные случайные величины………………………………….…70
Непрерывные случайные величины…………………………………..71
Совместное распределение дискретных случайных величин……….74
