5. Поняття матриці. Види матриці

Прямокутна матриця складена із довільного набору величин назив.прямокутною матрицею.Величини з яких складається матриця назив.елементами матриці.Сукупність елементів розміщених на горизонтальній(вертик.) прямій складають рядок(стовпець) матриці. Познач.великими латинськими літерами,а її елементи малими з двома індексами: а(№рядка) і J(№стовпця). МХN – розмірність матриць.

Види матриць:

1.квадратна – мат-я, в якій число рядків = числу стовпців.К-сть рядків(стовпців) назив.її порядком.

2.нульова – мат-я,всі елементи якої = нулю.

3.діагональна – квадратна матриця,всі елементи якої,крім діагональних,= нулю.

4.одинична – діагональна матриця,всі елементи головної діагоналі якої = одиниці(познач Е).

5.Матриця-рядок(матриця-стовпець) – матриця,яка склад.з одного рядка.

6.Трикутна – матриця в якої елементи, розміщені під головною діагоналлю = нулю.

7.Транспонована – матриця у якої рядки і стовпці поміняні місцями.

6.Транспонована матриця

Якщо у матриці А замінити стовпці так, щоб 1-й рядок став першим стовпцем, 2-й рядок став другим стовпцем і т. д., то дістанемо матрицю, яка називається транспонованою відносно матриці А (позначається А_т).

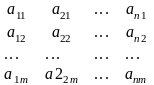
А_т =

- матриця, транспонована відносно А.

Перехід від А до А_т називається операцією транспону­вання.

7.Обернена матриця

Матриця А^-1 назив.оберненою до матриці А,якщо викон.рівності: АА^-1=А^-1А=Е

Якщо визначник матриці А ≠ 0,то матриця назив.неособливою(не виродженою).

Теорема 1. Для того,щоб матриця мала обернену необхідно і досить,щоб вона була не виродженою. Алгоритм:

1.Знайти визначник матриці А:|A|=∆

2.Знайти алгебраїчні доповнення елементів матриці матриці А.

3.Скласти матрицю з алгебраїчних доповнень елементів матриці А.

4.Транспонувати матрицю з алгебраїчних доповнень(назив.приєднаною або союзною,познач.вектор А)

5.Помножити приєднану матрицю на число 1/∆.

8. Операції над матрицями.

Прямокутна таблиця складена із довільного набору вели­чин називається прямокутною матрицею.

1⁰. Величини, з яких складається матриця, називаються елементами матриці.

2⁰. Суку­пність елементів, розміщених на горизонтальній (вертикальній) прямій складають рядок (стовпець) матриці.

3⁰. Матриці позначаються великими латинськими літерами, а її елементи малими латинськими з двома індексами, перший з яких вказує на номер рядка, а другий на номер стовпця, на пе­ретині яких цей елемент знаходиться.

4⁰. Символічний добуток числа рядків т на число стовпців п називають розміром матриці і позначають т×п.

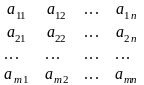
- матриця розміру т×т

Скорочене позначення матриці: А = (а_іj), і = 1,m, j = 1,п.

Основні властивості визначників

1. Визначник не зміниться, якщо рядки поміняти на відповідні стовпці, а стовпці – на рядки.

2. При перестановці двох рядків (або стовпців) абсолютна величина визначника не зміниться, а знак зміниться на протилежний.

3. Якщо всі елементи довільного рядка (або стовпця) дорівнюють нулю, то визначник також дорівнює нулю.

4. Визначник з двома однаковими рядками (або стовпцями) дорівнює нулю.

5. Якщо всі елементи довільного рядка (або стовпця) мають спільний множник, то його можна винести за знак визнач­ника.

6. Визначник, у якого всі елементи одного рядка або стовпця пропорційні відповідним елементам іншого рядка (або сто­впця), дорівнює нулю.

7. Якщо всі елементи деякого рядка (або стовпця) визначника є сумою двох доданків, то визначник дорівнює сумі двох визначників, у яких елементи згаданого рядка (стовпця) замінені відповідними доданками.

8. Визначник не зміниться, якщо до всіх елементів довільного рядка (стовпця) додати елементи іншого рядка (стовпця), помножені на довільний множник, відмінний від нуля.

9. Основні властивості визначників

1. Визначник не зміниться, якщо рядки поміняти на відповідні стовпці, а стовпці – на рядки.

2. При перестановці двох рядків (або стовпців) абсолютна величина визначника не зміниться, а знак зміниться на протилежний.

3. Якщо всі елементи довільного рядка (або стовпця) дорівнюють нулю, то визначник також дорівнює нулю.

4. Визначник з двома однаковими рядками (або стовпцями) дорівнює нулю.

5. Якщо всі елементи довільного рядка (або стовпця) мають спільний множник, то його можна винести за знак визнач­ника.

6. Визначник, у якого всі елементи одного рядка або стовпця пропорційні відповідним елементам іншого рядка (або сто­впця), дорівнює нулю.

7. Якщо всі елементи деякого рядка (або стовпця) визначника є сумою двох доданків, то визначник дорівнює сумі двох визначників, у яких елементи згаданого рядка (стовпця) замінені відповідними доданками.

8. Визначник не зміниться, якщо до всіх елементів довільного рядка (стовпця) додати елементи іншого рядка (стовпця), помножені на довільний множник, відмінний від нуля.