Активность системы

характеризует относительную активность упорядочивающих процессов в системе в виде баланса между химическим потенциалом и тепловой энергией. Используем (2.62)

,

находим

. (2.62б)

Для газа с поступательным движением частиц

. (2.62в)

При повышении температуры и уменьшении концентрации частиц активность понижается.

Для гелия при нормальных условиях

,

из (2.62а) и (2.62б) получаем

, .

Классический газ соответствует высоким температурам, низким концентрациям, большим расстояниям между частицы, когда преобладают силы притяжения, поэтому химический потенциал отрицательный и активность мала

, .

Распределение по состояниям максвелла–больцмана

В классической физике состояние совпадает с уровнем энергии. Частицы идеального газа на одном энергетическом уровне отличаются проекциями импульса и положениями в пространстве. Найдем среднее число частиц в одном состоянии для газа с фиксированной температурой и концентрацией.

Для трехмерного газа среднее число частиц в единице объема с энергией в интервале описывается распределением Максвелла по энергии (2.48а)

.

Концентрацию n выражаем через химический потенциал, используя (2.62а):

,

тогда

.

Множитель выражаем через энергетическую плотность состояний в единице объема (П.2.5)

.

В результате распределение Максвелла получает вид

, (П.7.6)

где среднее число частиц на уровне с энергией 

(П.7.7)

называется распределением по состояниям Максвелла–Больцмана, где

– активность системы.

Из (П.7.7) находим

,

активность равна среднему числу частиц в состоянии с .

Распределение по состояниям представляем наглядно на рисунке. Ось энергии направляем вертикально, уровни энергии изображаем горизонтальными линиями, частицы – точками. Из (П.7.7) следует:

1. Чем выше уровень энергии, тем меньше на нем частиц;

2. При повышении температуры заполненность верхних уровней повышается, нижних уровней понижается за счет переходов частиц снизу вверх.

3. При низкой температуре заполнены лишь нижние уровни.

4. Площадь под кривой пропорциональна температуре

.

Среднее число частиц в единичном интервале энергии около 

(П.7.8)

равно произведению числа состояний в единичном интервале энергии на число частиц в одном состоянии.

Для He при , ранее получено

, .

Из

(П.2.5)

для He с при ,

находим

,

,

.

Термодинамический потенциал Гиббса

Для описания системы с переменным числом частиц используется термодинамический потенциал Гиббса и омега-потенциал.

Определяем потенциал Гиббса

. (2.64)

Используем (2.61)

,

находим

, (2.65)

тогда

.

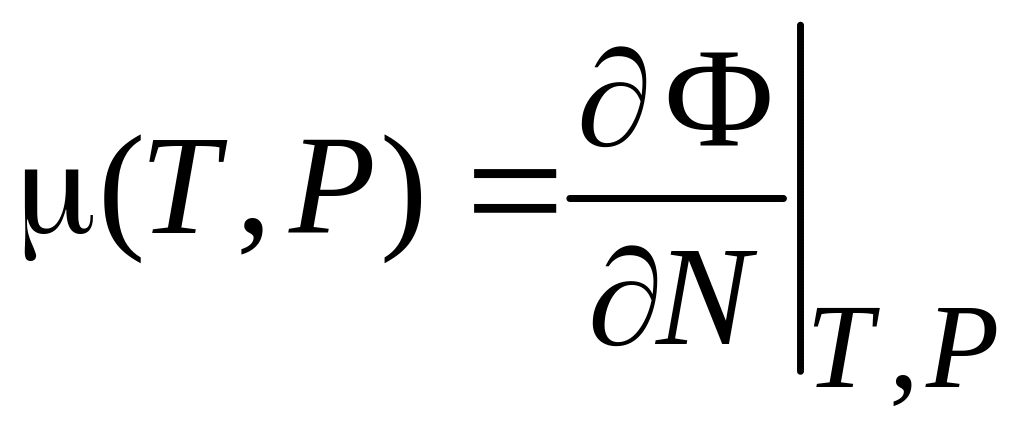При фиксированных P и T из (2.65) получаем

.

Интегрируем по N

. (2.66)

Здесь и далее число частиц является характеристикой макросостояния, поэтому . Термодинамический потенциал Гиббса равен химическому потенциалу, умноженному на среднее число частиц системы.

Из (2.64)

и (2.66) получаем

. (2.67)

-потенциал

Определяем

, (2.68)

где учтено (2.67). Следовательно, Ω-потенциал не зависит явно от числа частиц системы

.

Дифференцируем (2.68)

,

подставляем (2.61)

,

получаем

,

откуда

,

,

. (2.69)

В результате уравнение состояния системы

.

Получим выражение для Ω-потенциала через статистические характеристики системы.