
- •Распределение максвелла–больцмана
- •Распределение по координатам и импульсам
- •Распределение Максвелла
- •Распределение по импульсам
- •Распределение по скоростям
- •Средняя и средняя квадратичная проекции скорости
- •Распределение в сферических координатах
- •Распределение по модулю скорости
- •Наиболее вероятная энергия
- •Средняя энергия
- •Поток частиц
- •Поток импульса
- •Поток энергии
- •ВыТекание газа из отверстия сосуда в вакуум
- •Термоэлектронная эмиссия
- •Время выхода частицы из потенциальной ямы
- •Распределение Больцмана
- •Получение распределения
- •Формула Больцмана
- •Газ в центрифуге
- •Ориентационная поляризация диэлектрика
- •Термодинамические потенциалы Основные положения
- •Химический потенциал системы
- •Электрохимический потенциал
- •Внутренняя энергия
- •Равновесие двухфазной системы
- •Химический потенциал системы
- •Активность системы
- •Распределение по состояниям максвелла–больцмана
- •Термодинамический потенциал Гиббса
- •Большое каноническое распределение
- •Распределение микросостояний по фазовому пространству
- •Интеграл состояния
- •2. Распределение электронов у поверхности металла
- •3. Капля жидкости в насыщенном паре
- •4. Заряженная капля жидкости в насыщенном паре
- •Вопросы коллоквиума
- •Вопросы экзамена
Формула Больцмана
Объект.
Газ в однородном поле тяжести. Сила mg
действует на частицу вниз. Тепловая
энергия
![]() раскидывает частицы по разным высотам.
Концентрация
раскидывает частицы по разным высотам.
Концентрация
![]() уменьшается с высотой z.
уменьшается с высотой z.
Количественное описание. Потенциальная энергия частицы
![]() ,
,
где m – масса частицы. Для концентрации получаем из (2.56а) формулу Больцмана
![]() ,
(П.6.1)
,
(П.6.1)
![]() – концентрация
при
– концентрация
при
![]() .
.
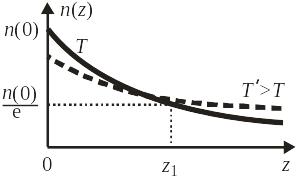
Если N частиц заполняют цилиндр 0 z < с поперечным сечением S, тогда вероятность обнаружить частицу в интервале
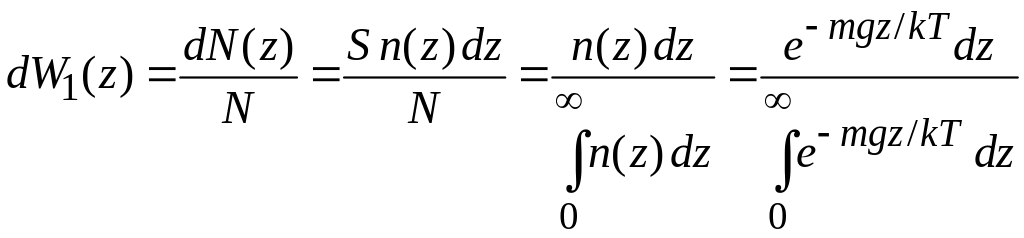 ,
(П.6.2)
,
(П.6.2)
где
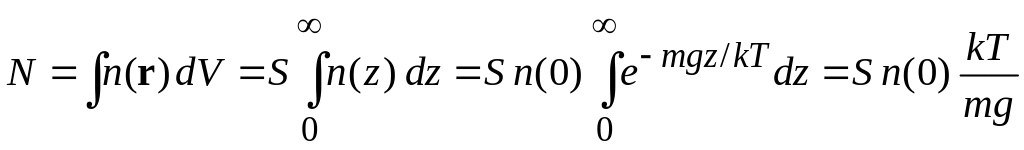 .
.
Получаем концентрацию при
![]() ,
,
и около точки z
![]() .
.
При
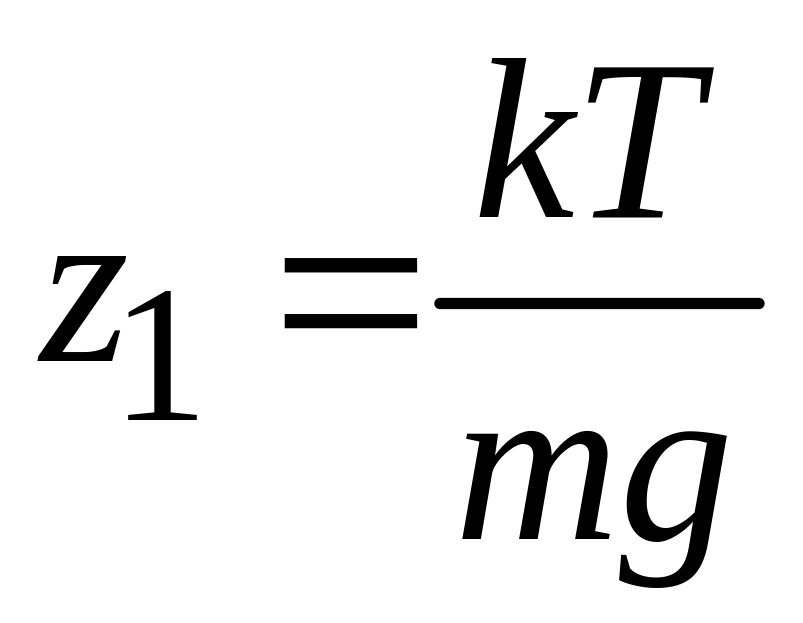 находим
находим
![]() ,
где
,
где
![]() – основание неперовых логарифмов.
– основание неперовых логарифмов.
Площадь под кривой
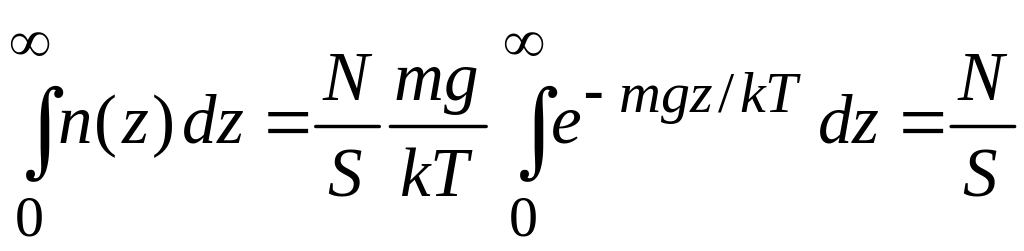 .
.
Среднее положение частицы
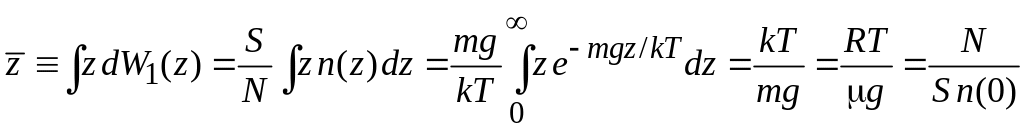 ,
,
где использовано
![]() ,
(5.6.2)
,
(5.6.2)
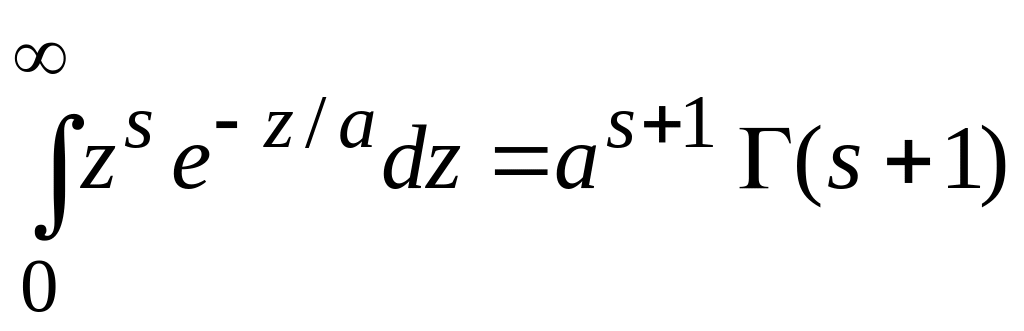 ,
,
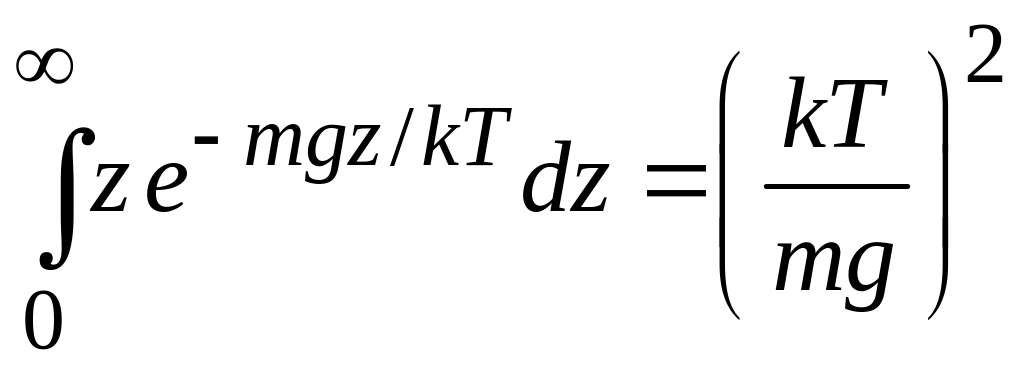 .
.
Число частиц в цилиндре
![]() .
.
Средняя
потенциальная энергия частицы с учетом
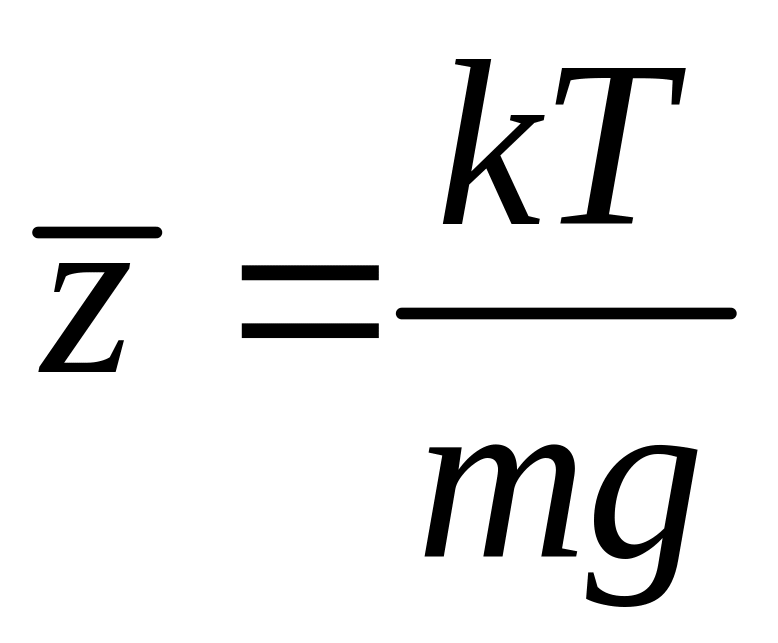 равна
равна
![]() .
.
Этот результат следует также из теоремы (2.38) и (2.39) о распределении тепловой энергии по степеням свободы. Для одной степени свободы
![]() ,
,
![]() .
.
Для
потенциальной энергии
подставляем
![]() .
.
Частные
значения.
При T
= 300К
для воздуха
= 29 кг/кмоль получаем
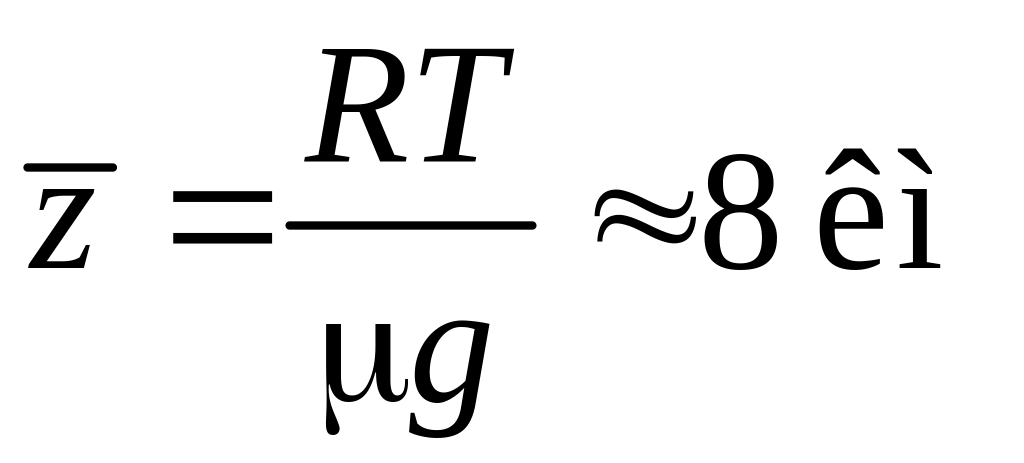 .
Число частиц в столбе воздуха с единичным
поперечным сечением выражаем через
давление
.
Число частиц в столбе воздуха с единичным
поперечным сечением выражаем через
давление
![]() .
Для Р
= 760 мм р.с. находим
.
Для Р
= 760 мм р.с. находим
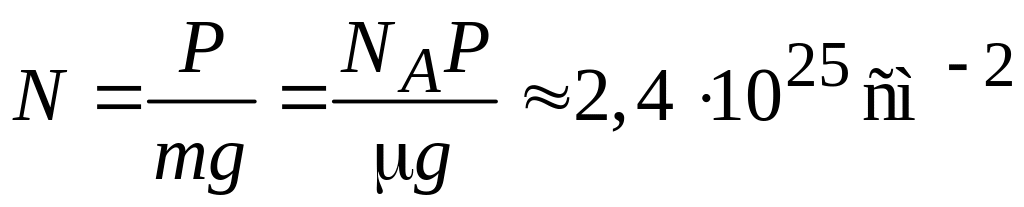 .
.
Концентрация молекул у поверхности земли – число Лошмидта
![]() .
.
Газ в центрифуге
Объект. Центрифуга – цилиндрический сосуд с газом радиусом R, длиной образующей H, вращается вокруг оси с угловой скоростью . В системе отсчета сосуда на молекулы действует центробежная сила инерции, направленная от оси вращения. В результате концентрация газа увеличивается с удалением от оси.
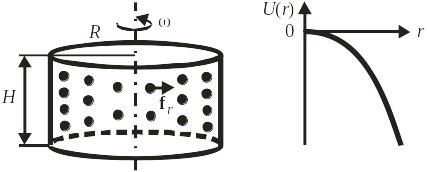
Количественное описание. В системе отсчета, связанной с вращающимся сосудом, центробежная сила
![]()
создает потенциальную энергию. Используем
![]() ,
,
![]() ,
,
находим потенциальную энергию частицы массой m, находящейся на расстоянии r от оси:
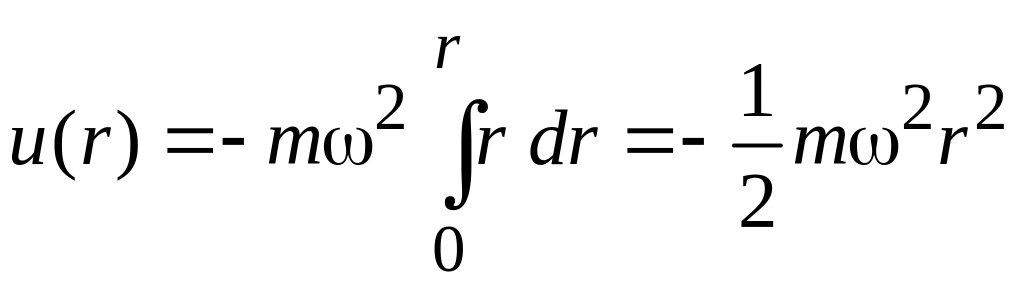 .
.
Распределение Больцмана (2.55)
![]()
в цилиндрических координатах
![]() ,
,
![]()
дает
![]() .
.
Интегрируем по z и φ, и получаем вероятность нахождения частицы в цилиндрическом слое радиусом r толщиной dr
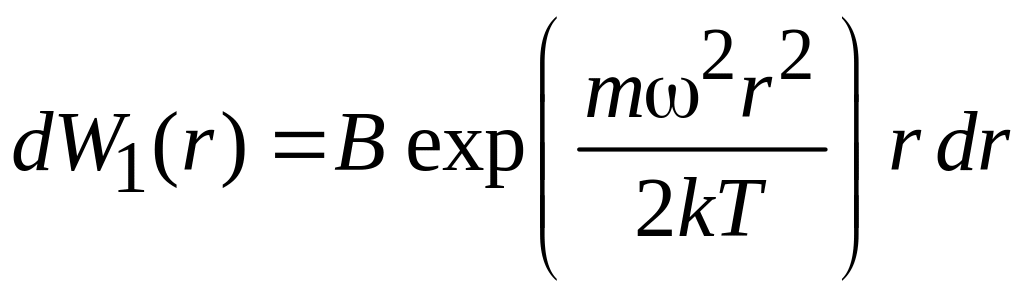 (П.6.2)
(П.6.2)
Вероятность найти частицу в единице объема на расстоянии r от оси
![]() ,
,
где объем цилиндрического слоя радиусом r толщиной dr
![]() .
.
Концентрация частиц
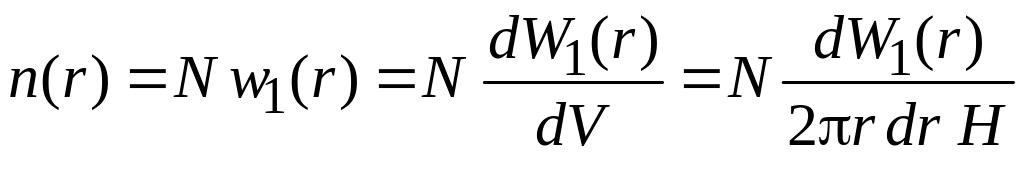 ,
,
где N – число частиц в центрифуге. Учитывая (П.6.2), получаем
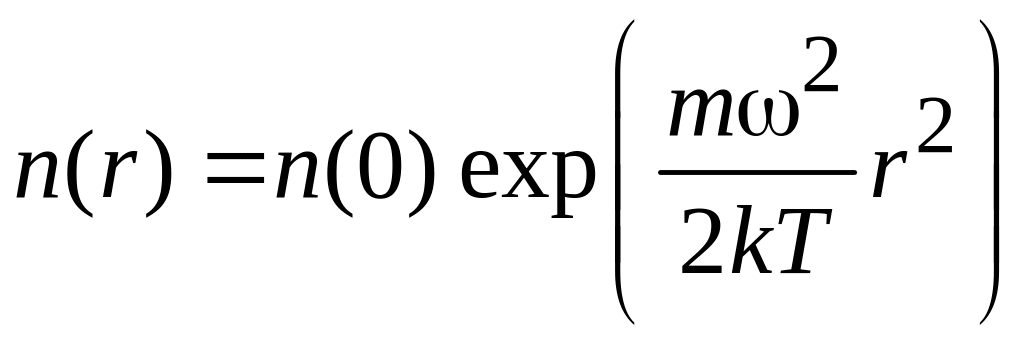 ,
(П.6.3)
,
(П.6.3)
где
– концентрация на оси вращения;
![]() – увеличивается
при удалении от оси.
– увеличивается
при удалении от оси.
Условие нормировки на число частиц
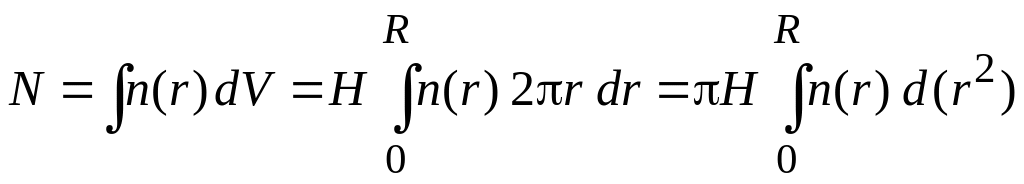
с учетом (П.6.3) дает
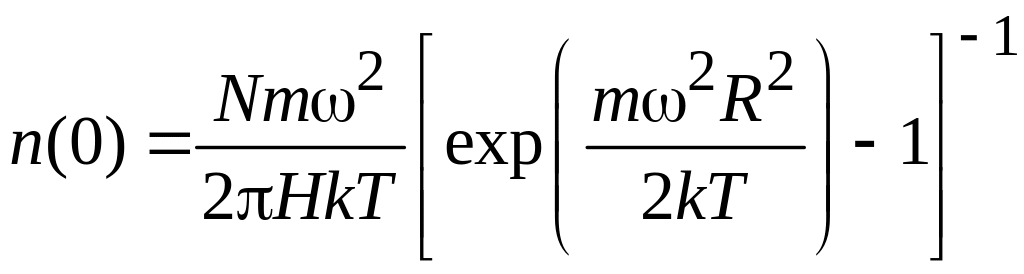 .
(П.6.4)
.
(П.6.4)
Ориентационная поляризация диэлектрика
Объект.
Молекула полярного
диэлектрика
(например, H2S)
имеет электрический дипольный момент
с модулем
![]() ,
где q
– модуль заряда иона; l
– расстояние между ионами. Диполи разных
молекул направлены по всем направлениям.
Внешнее электрическое поле
,
где q
– модуль заряда иона; l
– расстояние между ионами. Диполи разных
молекул направлены по всем направлениям.
Внешнее электрическое поле
![]() поворачивает диполи и устанавливает
их вдоль поля, возникает ориентационная
поляризация. Тепловое движение
разбрасывает направления диполей.
Средняя проекция дипольного момента
на направление поля определяет поляризацию
диэлектрика, т. е. дипольный момент
единицы объема.
поворачивает диполи и устанавливает
их вдоль поля, возникает ориентационная
поляризация. Тепловое движение
разбрасывает направления диполей.
Средняя проекция дипольного момента
на направление поля определяет поляризацию
диэлектрика, т. е. дипольный момент
единицы объема.
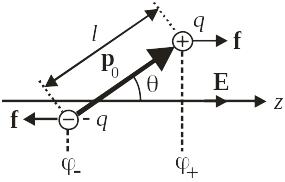
Количественное описание. В однородном электрическом поле Е, направленном по оси z, потенциальная энергия диполя
![]() .
.
Доказательство:
Электрическое поле направлено в сторону быстрейшего убывания потенциала. В однородном поле на рисунке потенциал точки z
![]() .
.
Эквипотенциальные поверхности перпендикулярны оси z
![]() .
.
Для заряда q потенциальная энергия
![]() ,
,
тогда энергия диполя
![]() ,
,
где
![]() ,
,
![]() .
.
Для получения средней проекции дипольного момента используем распределение Больцмана (2.55)
.
Выбираем сферические координаты с осью z, направленной по полю, тогда
![]() .
.
Потенциальная
энергия
![]() не зависит от радиуса. Интегрируем
(2.55)
по радиусу и получаем
не зависит от радиуса. Интегрируем
(2.55)
по радиусу и получаем
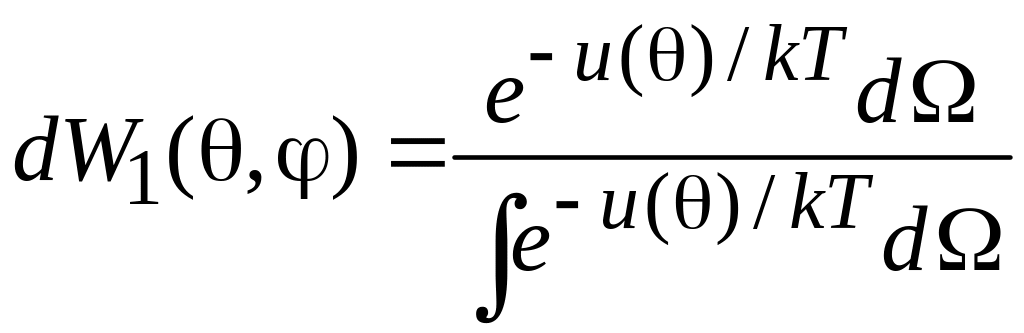 ,
,
где элемент телесного угла
![]() .
.
Потенциальная энергия не зависят от угла φ. Интегрируем по φ
![]() ,
,
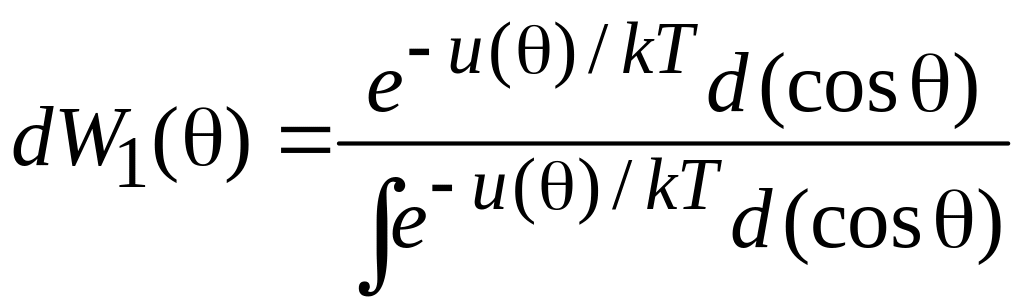 ,
,
.
Упрощаем выражения, вводя:
![]() – относительная
энергия взаимодействия,
– относительная
энергия взаимодействия,
![]() ,
,
![]() .
.
Получаем
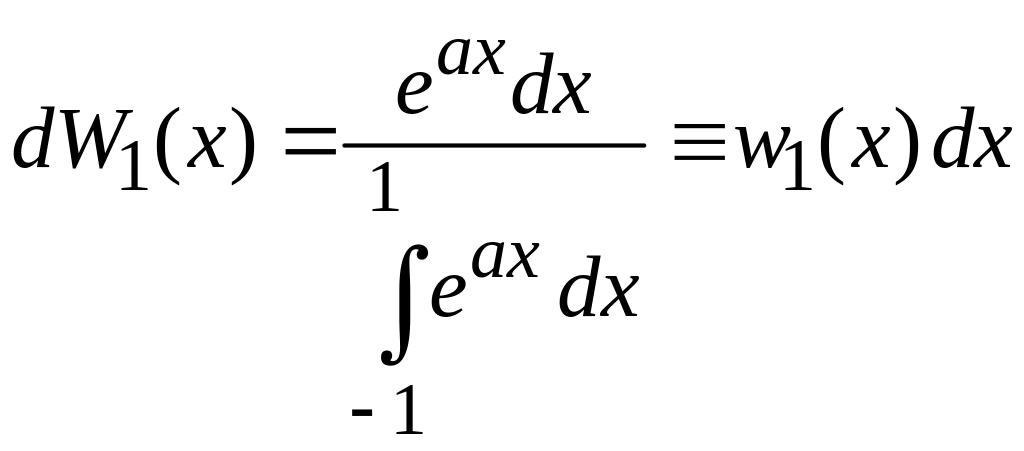 .
.
Используем
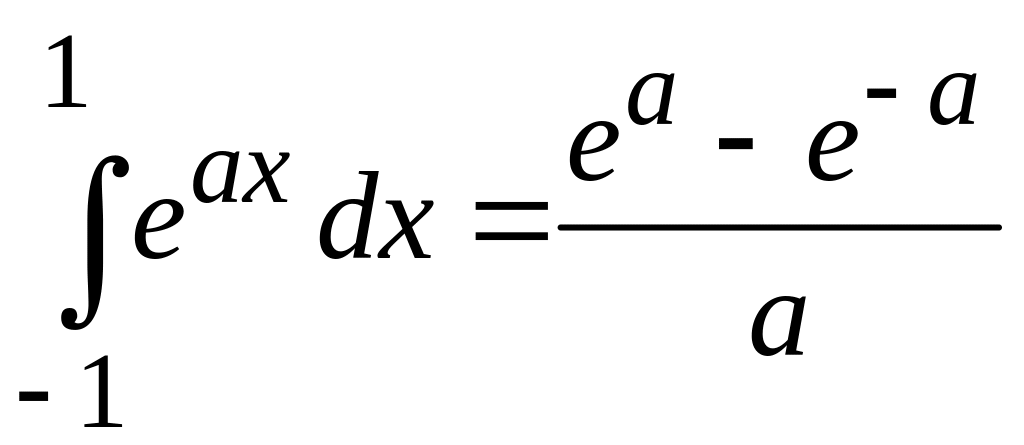 ,
,
находим функцию распределения ориентаций дипольного момента
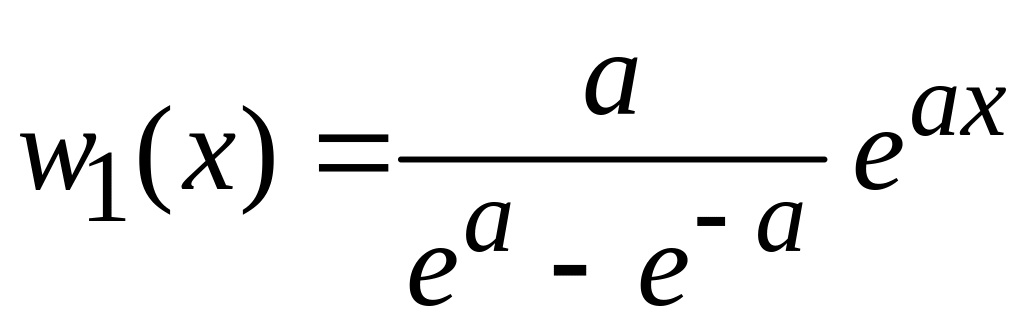 .
(П.6.5)
.
(П.6.5)
Средняя проекция дипольного момента
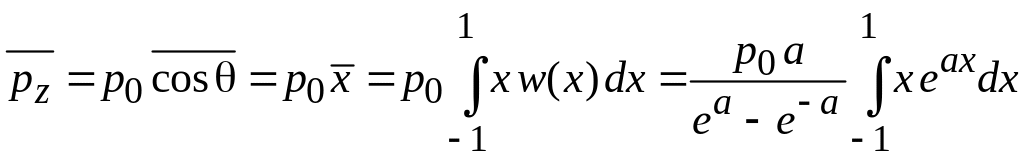 .
.
Интегрируем по частям
![]() ,
,
![]() ,
,
![]() ,
,
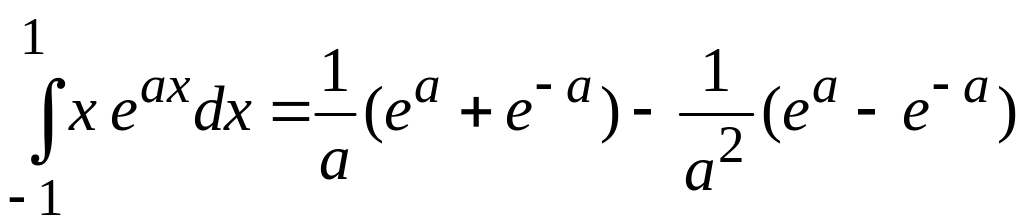 .
.
Получаем
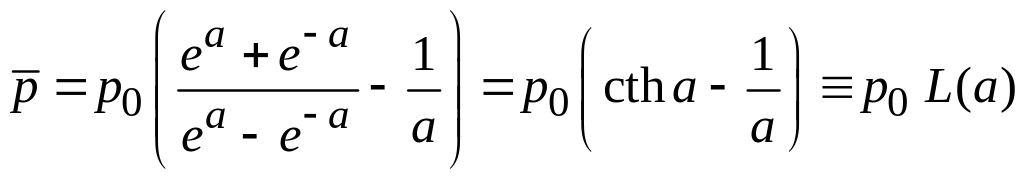 ,
(П.6.6)
,
(П.6.6)
где L(a) – функция Ланжевена.
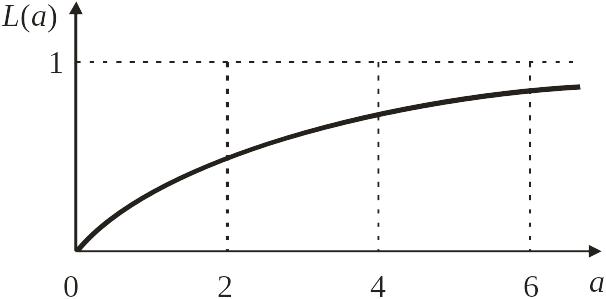
В слабом поле
![]() ,
,
![]() ,
,
разлагаем в ряд
![]() ,
,
получаем
![]() ,
,
,
,
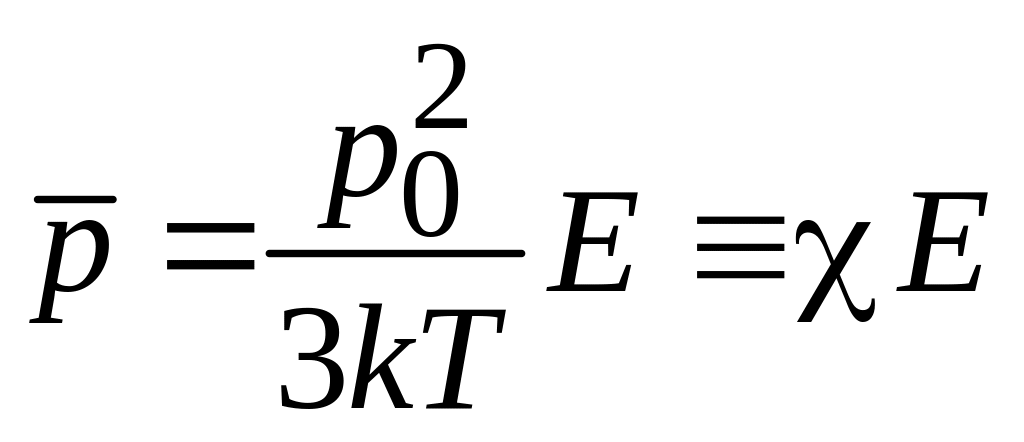 ,
,
где
ориентационная поляризуемость
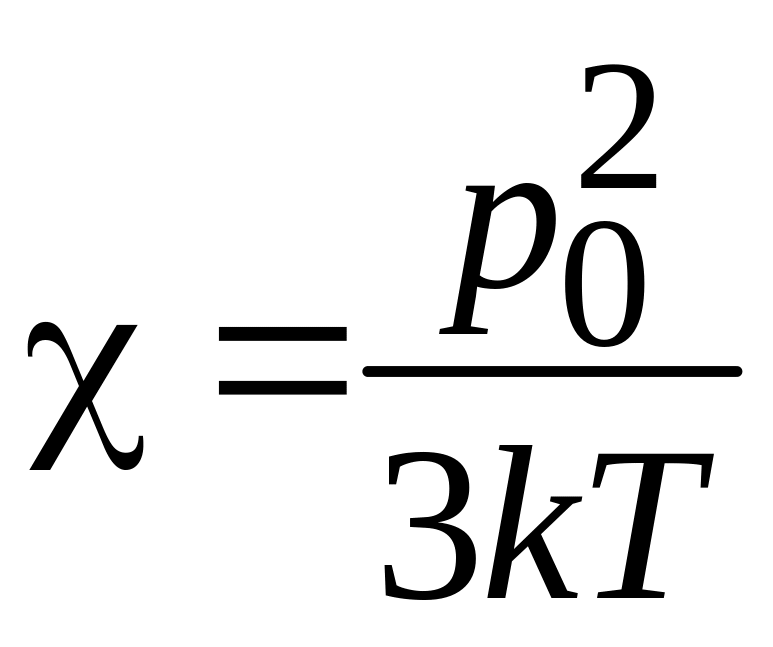 обратно пропорциональна температуре.
обратно пропорциональна температуре.
В сильном поле
![]() ,
,
![]() ,
,
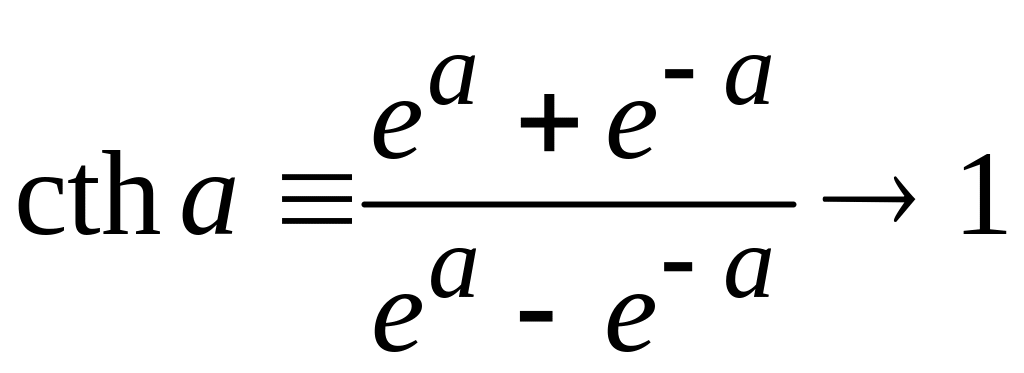 ,
,
![]() ,
,
![]()
– все диполи ориентированы по полю, как показано на рисунке. Возникает насыщение намагниченности.
Поль Ланжевен разработал статистическую теорию парамагнетизма в 1905 г. и получил результат, аналогичный (П.6.6).
Петер Дебай применил в 1911 г. статистический метод Ланжевена для поляризации диэлектриков и назвал функцию (П.6.6) именем Ланжевена.
В честь Дебая названа внесистемная единица электрического дипольного момента
1 Д (дебай) = 110–18 ед. СГС = 3,3356410–30 Клм.


Поль Ланжевен (1872–1946) Петер Дебай (1884–1966)
