
- •Распределение максвелла–больцмана
- •Распределение по координатам и импульсам
- •Распределение Максвелла
- •Распределение по импульсам
- •Распределение по скоростям
- •Средняя и средняя квадратичная проекции скорости
- •Распределение в сферических координатах
- •Распределение по модулю скорости
- •Наиболее вероятная энергия
- •Средняя энергия
- •Поток частиц
- •Поток импульса
- •Поток энергии
- •ВыТекание газа из отверстия сосуда в вакуум
- •Термоэлектронная эмиссия
- •Время выхода частицы из потенциальной ямы
- •Распределение Больцмана
- •Получение распределения
- •Формула Больцмана
- •Газ в центрифуге
- •Ориентационная поляризация диэлектрика
- •Термодинамические потенциалы Основные положения
- •Химический потенциал системы
- •Электрохимический потенциал
- •Внутренняя энергия
- •Равновесие двухфазной системы
- •Химический потенциал системы
- •Активность системы
- •Распределение по состояниям максвелла–больцмана
- •Термодинамический потенциал Гиббса
- •Большое каноническое распределение
- •Распределение микросостояний по фазовому пространству
- •Интеграл состояния
- •2. Распределение электронов у поверхности металла
- •3. Капля жидкости в насыщенном паре
- •4. Заряженная капля жидкости в насыщенном паре
- •Вопросы коллоквиума
- •Вопросы экзамена
Средняя и средняя квадратичная проекции скорости
Средняя проекция скорости
 .
.
Гамильтониан зависит от квадрата скорости, поэтому направления по- и против оси x равноправные.
Средняя квадратичная проекция скорости
 ,
(2.42б)
,
(2.42б)
где
 .
.
Доказательство:
Подставляем (2.42а)
 ,
,
находим
 ,
,
где использовано
 ,
,
![]() ,
,
,
,
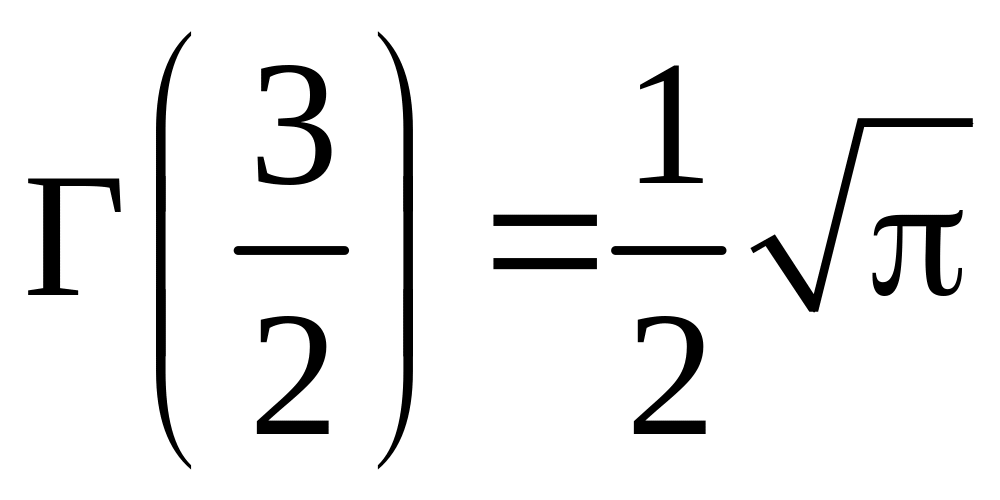 .
.
Распределение в сферических координатах
В распределении (2.41)
переходим от декартовых координат к сферическим. Заменяем
![]() ,
,
![]() ,
,
![]() .
.
Получаем вероятность обнаружения частицы с модулем скорости в интервале от v до (v+dv), движущуюся в интервале углов от (, ) до (+d, +d)
 ,
(2.43)
,
(2.43)
где
![]() – концентрация частиц со скоростями
от (v,
,
)
до (v+dv,
+d,
+d);
n
– концентрация частиц со всеми скоростями.
– концентрация частиц со скоростями
от (v,
,
)
до (v+dv,
+d,
+d);
n
– концентрация частиц со всеми скоростями.
Распределение по модулю скорости
Интегрируем
(2.43) по углам, учитывая
![]() :
:
 (2.44)
(2.44)
– вероятность
обнаружения частицы с модулем скорости
от v
до
![]() ,
,
 (2.44а)
(2.44а)
– функция
распределения по модулю скорости
– относительное
число частиц с модулем скорости в
единичном интервале около
![]() ;
;
dn(v) – концентрация частиц с модулем скорости от v до ;
![]() – концентрация
частиц с модулем скорости в единичном
интервале около v.
– концентрация
частиц с модулем скорости в единичном
интервале около v.

Условие нормировки
 ,
,
площадь под кривой – единица.
С ростом температуры максимум распределения понижается, кривая сдвигается вправо, увеличивается вероятность обнаружить частицу с большей скоростью, площадь под кривой сохраняется.
Наиболее вероятная скорость
Максимум функции распределения
![]() ,
,

с учетом функции (2.44а)
соответствует наиболее вероятной скорости
 (2.45)
(2.45)
Средняя скорость
Из теории вероятности
 .
.
Подставляем (2.44а)
 ,
,
находим
 .
(2.46)
.
(2.46)
При вычислении использовано
,
![]() ,
,
,
,
![]() .
.
Средняя квадратичная скорость
Используя
 .
.
аналогично находим
 .
(2.47)
.
(2.47)
Распределение по энергии
В распределении по модулю скорости (2.44)
заменяем
 ,
,
 ,
,
 ,
,
где ε – кинетическая энергия частицы. Получаем
 ,
(2.48)
,
(2.48)
где функция распределения Максвелла по энергии
 (2.48а)
(2.48а)
– относительное число частиц с энергией в единичном интервале около ε;
![]() – концентрация
частиц с энергией от ε до e
+ de;
– концентрация
частиц с энергией от ε до e
+ de;
![]() – концентрация
частиц с энергией в единичном интервале
около
– концентрация
частиц с энергией в единичном интервале
около
![]() .
.
Выполняется нормировка
 ,
,
![]() .
.

Площадь под кривой – единица;
с ростом Т максимум понижается, сдвигается вправо и увеличивается вероятность обнаружить частицу с большей энергией.


