3.2.2. Термомеханические (биметаллические, или биморфные) актюаторы

Принцип действия этих актюаторов основан на термомеханическом эффекте преобразования энергии нагревания в механическую силу деформирования элемента, сочетающего два адгезионно связанных разнородных материала с различными термическими коэффициентами расширения при заданных теплоемкости и теплопроводности, обеспечивающих требуемое изменение температуры и, соответственно, требуемое время отклика. Это делает их простой альтернативой актюаторам для МЭМП и НЭМП, работающим на других принципах. Уменьшение масштаба облегчает достижение нужных эффектов в термических актюаторах, хотя теплообмен в микро- и наномасштабе в них может создавать определенные проблемы. Однако, сочетание способности таких актюаторов создавать значительные усилия и смещения при сравнительно малых разностях температур обусловливает большой интерес, проявляемый к ним. Они представляют собой обычный упругий элемент, балка которого, состоящая из двух тонких слоев разнородных материалов, например, допированного кремния и его диэлектрических производных (оксидов или нитридов) или кремния и благородных металлов (золота, платины), одновременно выполняет функцию упругого элемента и актюатора.

В случае биморфной консольной балки длиной l, шириной в и толщиной а смещение ее конца (прогиб) Δz при изменении температуры на величину ΔТ и равномерном распределении тепла определяется соотношением: 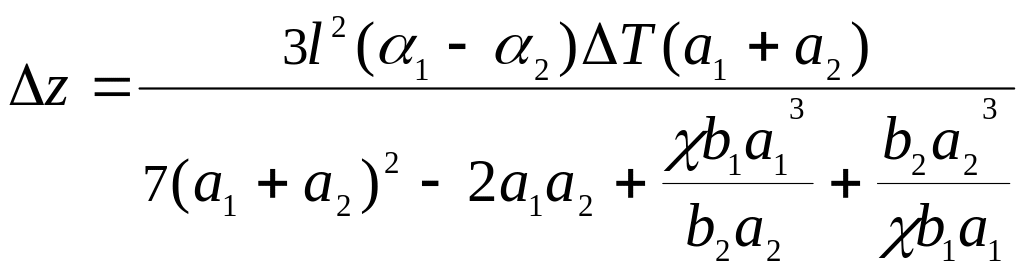, где α – термический коэффициент линейного расширения, . Индекс 1 относится к слою с меньшим значением термического коэффициента расширения α, 2 – с большим. Радиус кривизны балки определяется по нейтральной оси, лежащей на границе раздела слоев, причем, при α₁›α₂, слой 1 располагается с вогнутой стороны, а слой 2 – с выпуклой. Из этого соотношения видно, что из-за достаточно малой разности термических коэффициентов и модулей упругости используемых материалов основные возможности в получения заданного смещения конца балки лежат в варьировании ее геометрических параметров, в первую очередь, длины и толщины. Анализ этого уравнения показывает, что максимальная величина Δz наблюдается при одинаковых минимальных значениях толщины а и ширины в обоих слоев и максимальной длине балки. При а₁=а₂=в₁=в₂=а уравнение принимает вид: 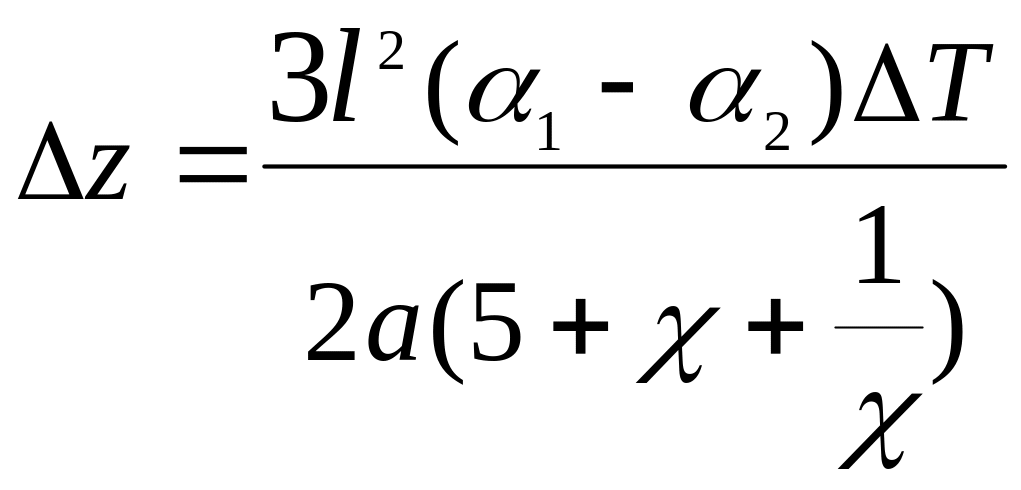. Развиваемое при этом усилие на ее конце может быть рассчитано через коэффициент жесткости : 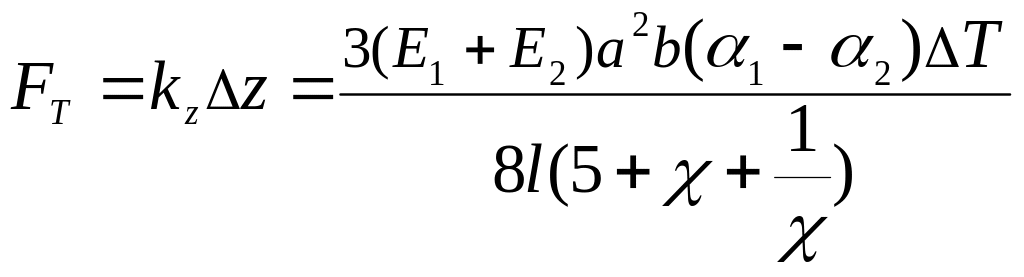, где Е* - эффективный модуль упругости двухслойной балки, который, в первом приближении, рассчитан по простому правилу аддитивности с учетом долей толщины слоев в общей толщине , где и . Из общего скейлингового (масштабного) анализа этого соотношения следует, что масштабный коэффициент термической упругой силы равен 2, т.е. изменение силы, при прочих заданных условиях, пропорционально квадрату выбранного линейного размера [L²].

Для приведенной на рисунке 27 консольно-закрепленной двухслойной балки

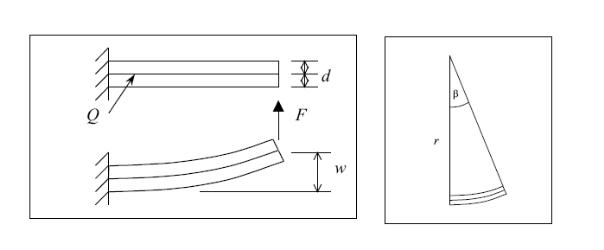
Рис.27. Схема изгиба консольно-закрепленной двухслойной балки при подводе тепла Q.

смещение конца балки w при действии на него силы F равно: , где -момент инерции сечения ( ). Тогда при ΔТ=15 К, α₁ =24х10^-6 К^-1, α₂ =12х10^-6 К^-1, Y₁=72,2 ГПа, Y₂=210 ГПа, квадратном сечении балки со стороной d=5 мм, и длиной l=50 мм в первом слое возникает сила F₁=12,1 Н, а во втором – F₂=4 Н. При этом скорость развития усилия (время отклика) скоростью и равномерностью нагрева и охлаждения.

Очевидно, что при статических условиях работы для поддержания заданной температуры балки необходимы минимальные теплопотери. Наоборот, при динамических условиях необходима максимальная скорость теплоотвода, чтобы тепловая постоянная времени, соответствующая времени отклика , где G и Н – теплопроводность и теплоемкость структуры соответственно, не превышала периода колебаний. Если исключить конвективный теплообмен и учитывать только ИК-излучение, то это время может быть определено по уравнению Стефана-Больцмана: , где m и с_р – масса балки и аддитивная удельная теплоемкость ее материалов соответственно; σ_в – константа, равная 5,67х10^-8 Вт/м²К⁴, ε_m – излучательная способность материала, А – площадь поверхности, Т₀ – начальная температура. Расчеты показывают, что в наномасштабе можно получить тепловую постоянную времени в пределах , что позволит использовать тепловую активацию в наносистемах. Трудной проблемой при этом становится создание теплового импульса. Более перспективным по сравнению с нагревом за счет омического сопротивления рассматривается использование радиационного нагревания, например, за счет лазерных импульсов [].

Наряду с плоско-параллельными биморфными микро- и наноструктурами в качестве термомеханических балочных актюаторов в настоящее время перспективными считаются упруго-шарнирные плоские структуры, сочетающие V-образные, или трапецевидные слои адгезионно связанных разнородных материалов с резко различными модулями упругости и термическими коэффициентами расширения или усадки (Рис.28-29).

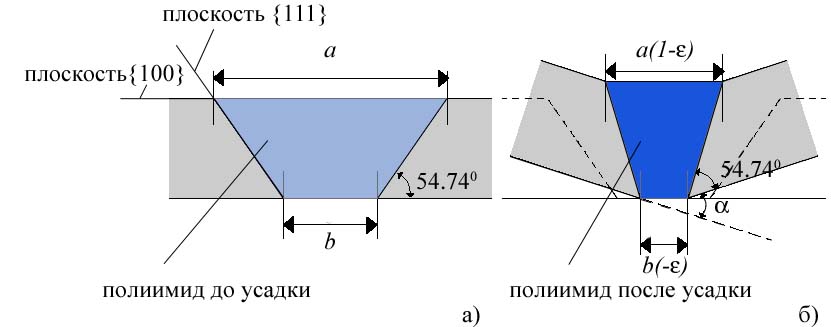
Рис.28. Схематическое изображение трапецевидной упруго-шарнирной структуры кремний-полиимид до (а) и после (б) усадки полиимида.

а)

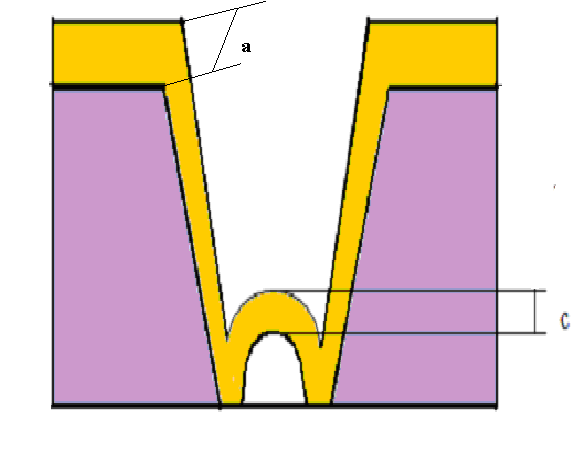
б)

Рис. 29. Схематические изображения трапецевидной упруго-шарнирной структур на основе жесткого и податливого материалов: а) - вид сверху и сбоку соответственно; б) – увеличенное сечение профиля податливого слоя, соединяющего трапецевидные слои жесткого материала.

Важное значение при разработке и использовании термических биморфных актюаторов, особенно при их работе в динамических условиях, имеет проблема их усталостной выносливости и долговечности, обусловленная частым перепадом температур и высоким уровнем возникающих напряжений и изгибных деформаций при наличии границы раздела между неоднородными материалами.