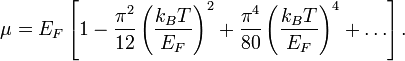Понятие о квантовой статистике Ферми-Дирака

1.Функция распределения Ферми-Дирака.

Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет распределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии; предложена в 1926 году итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком, который выяснил её квантово-механический смысл; позволяет найти вероятность, с которой фермион занимает данный энергетический уровень.

Работы по статистике Ферми — Дирака были опубликованы в 1926 году, а в 1927 она была применена Арнольдом Зоммерфельдом к электронам в металле.

В статистике Ферми — Дирака среднее число частиц в состоянии с энергией ε_i есть

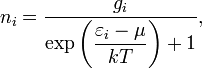
где

n_i — среднее число частиц в состоянии i,

ε_i — энергия состояния i,

g_i — кратность вырождения состояния i (число состояний с энергией ε_i),

μ — химический потенциал (который равен энергии Ферми E_F при абсолютном нуле температуры),

k — постоянная Больцмана,

T — абсолютная температура.

В (идеальном) ферми-газе в пределе низких температур μ = E_F. В этом случае (полагая уровни энергии невырожденными g_i = 1), функция распределения частиц называется функцией Ферми:

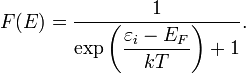
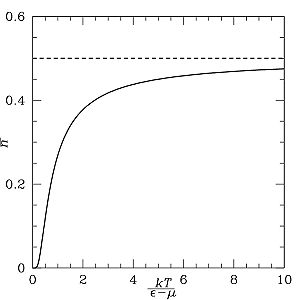
Распределение Ферми — Дирака как функция температуры. Заполнение уровней с энергиями растёт с увеличением температуры.

Применение

Статистики Ферми — Дирака и Бозе — Эйнштейна применяются в том случае, когда необходимо учитывать квантовые эффекты, когда частицы обладают «неразличимостью». Квантовые эффекты проявляются тогда, когда концентрация частиц (где n_q — квантовая концентрация).

Квантовая концентрация — это концентрация, при которой расстояние между частицами соразмерно с длиной волны де Бройля, то есть когда волновые функции частиц соприкасаются, но не перекрываются. Квантовая концентрация зависит от температуры. Статистика Ферми — Дирака (Ф — Д) применяется к фермионам (частицы, на которые действует принцип Паули), статистика Бозе — Эйнштейна (Б — Э) применяется к бозонам. Оба этих распределения становятся распределением Максвелла — Больцмана при высоких температурах и низких концентрациях.

Распределением Максвелла — Больцмана часто описываются классические «различимые» частицы. Другими словами, конфигурация частицы A в состоянии 1 и частицы B в состоянии 2 отличается от конфигурации частицы B в состоянии 1 и частицы A в состоянии 2. Когда эта идея была проработана полностью, оказалось, что распределение частиц по энергетическим состояниям приводит к нефизическим результатам для энтропии, что известно, как парадокс Гиббса. Эта проблема исчезла, когда стал ясен тот факт, что все частицы неразличимы. И Ф — Д, и Б — Э приближаются к статистике Максвелла — Больцмана в пределе высоких температур и низких плотностей. Статистика Максвелла — Больцмана хорошо описывает поведение газов. Ф — Д часто используется для описания электронов в твердых телах, на ней, к примеру, базируются основные положения теории полупроводников в частности и электроники в целом.

Вывод распределения

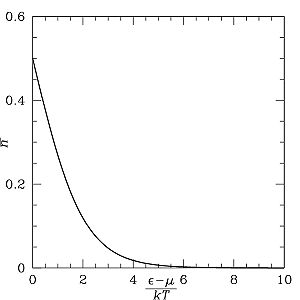
Распределение Ферми — Дирака как функция от . Высокоэнергетические состояния имеют меньшую вероятность. Или, низкоэнергетические состояния более вероятны.

Рассмотрим состояние частицы в системе, состоящей из множества частиц. Энергия такой частицы равна ε. Например, если наша система — это некий квантовый газ в «ящике», то подобное состояние может описываться частной волновой функцией. Известно, что для большого канонического ансамбля, функция распределения имеет вид

Z =	∑	e − (E(s) − μN(s)) / kT,
	s

где

E(s) — энергия состояния s,

N(s) — число частиц, находящихся в состоянии s,

μ — химический потенциал,

s — это индекс, пробегающий все возможные микросостояния системы.

В данном контексте, система имеет фиксированные состояния. Итак, если какое либо состояние занято n частицами, то энергия системы — . Если состояние свободно, то энергия имеет значение 0. Будем рассматривать равновесные одночастичные состояния как резервуар. После того, как система и резервуар займут одно и то же физическое пространство, начинает происходить обмен частицами между двумя состояниями (фактически, это явление мы и исследуем). Отсюда становится ясно, почему используется описанная выше функция распределения, которая, через химический потенциал, учитывает поток частиц между системой и резервуаром.

Для фермионов, каждое состояние может быть либо занято одной частицей, либо свободно. Поэтому, наша система имеет два множества: занятых (разумеется, одной частицей) и незанятых состояний, обозначающихся s₁ и s₂ соответственно. Видно, что E(s₁) = ε, N(s₁) = 1, и E(s₂) = 0, N(s₂) = 0. Поэтому функция распределения принимает вид:

Для большого канонического ансамбля, вероятность того, что система находится в микросостоянии s_α вычисляется по формуле

Наличие состояния, занятого частицей, означает, что система находится в микросостоянии s₁, вероятность которого

называется распределением Ферми — Дирака. Для фиксированной температуры T, есть вероятность того, что состояние с энергией ε будет занято фермионом. Обратите внимание, что является убывающей функцией от ε. Это соответствует нашим ожиданиям: высокоэнергетические состояния занимаются с меньшей вероятностью.

Обратите внимание, что энергетический уровень ε имеет вырождение g_ε. Теперь можно произвести простую модификацию:

Это число — ожидаемое число частиц, в суммарном состоянии с энергией ε.

Для всех температур T, . Это означает, что состояния с энергией μ всегда будут иметь одинаковую вероятность быть заполненными или свободными.

В пределе , становится ступенчатой функцией (см. первый график). Все состояния с энергией меньше химического потенциала μ будут заняты с вероятностью 1. Состояния с энергией выше химического потенциала μ будут свободны. Химический потенциал при нулевой температуре — энергия Ферми, обозначается E_F, то есть E_F = μ(T = 0).

Влияние температуры

Необходимо заметить, что химический потенциал зависит от температуры. Однако для систем, имеющих температуру ниже температуры Ферми , что часто используется, как аппроксимация . В реальности же: