Определение кривизны предварительно напряженных элементов на основе нелинейной деформационной модели

4.25. Значение кривизны принимают равным

(4.41)

где ε_b,max - максимальная относительная деформация сжатого бетона, определяемая на основе положений, приведенных в пп.3.26-3.29;

х - высота сжатой зоны в направлении, нормальном к нейтральной оси.

При этом для элемента с трещинами в растянутой зоне напряжение в арматуре, пересекающей трещину, определяют по диаграммам на черт.3.11-3.13 в зависимости от деформации арматуры равной

ε_s = ε_sm + 0,8ε_s,crc , (4.42)

где ε_sm - усредненная в пределах между трещинами относительная деформация арматуры, растянутой от внешней нагрузки, соответствующая линейному закону распределения деформаций по сечению;

ε_s,crc - относительная деформация арматуры в трещине от действия нагрузки, соответствующей образованию трещин.

При наличии трещин напряженно-деформированное состояние сжатого бетона определяется по двухлинейной диаграмме σ_b – ε_b (см. черт.3.10) с использованием приведенного модуля деформации сжатого бетона E_b,red определяемого согласно п.4.24, и значений ε_bl,red и ε_b2 принимаемых по табл.4.6.

При отсутствии трещин напряженно-деформированное состояние сжатого бетона определяется по трехлинейной диаграмме (черт.4.11), где ; ε_b0 и ε_b2 - см. табл.4.6; Е_b1 принимается равным: при непродолжительном действии нагрузки - Е_b, при продолжительном действии нагрузки - по формуле (4.34). Напряженно-деформированное состояние растянутого бетона также определяется по трехлинейной диаграмме (см. черт.4.11) с заменой R_b,ser на R_bt,ser, ε_b0 на ε_bt0 , ε_b2 на ε_bt2, где значения ε_bt0 и ε_bt2 - см табл.4.6.

Таблица 4.6

Характер действия нагрузки	Относительные деформации бетона
	при сжатии			при растяжении
	εb0·103	εb2·103	εb1,red ·103	εbt0·103	εbt2·103	εbt1,red·103
непродолжительное	2,0	3,5	1,5	0,10	0,15	0,08
продолжительное при относительной влажности окружающего воздуха, %
выше 75	3,0	4,2	2,4	0,21	0,27	0,19
40-75	3,4	4,8	2,8	0,24	0,31	0,22
ниже 40	4,0	5,6	3,4	0,28	0,36	0,26

При расчете статически неопределимых конструкций с учетом физической нелинейности для отдельных участков элементов используются жесткости, равные , где М - максимальный момент на рассматриваемом участке , соответствующая этому моменту кривизна .

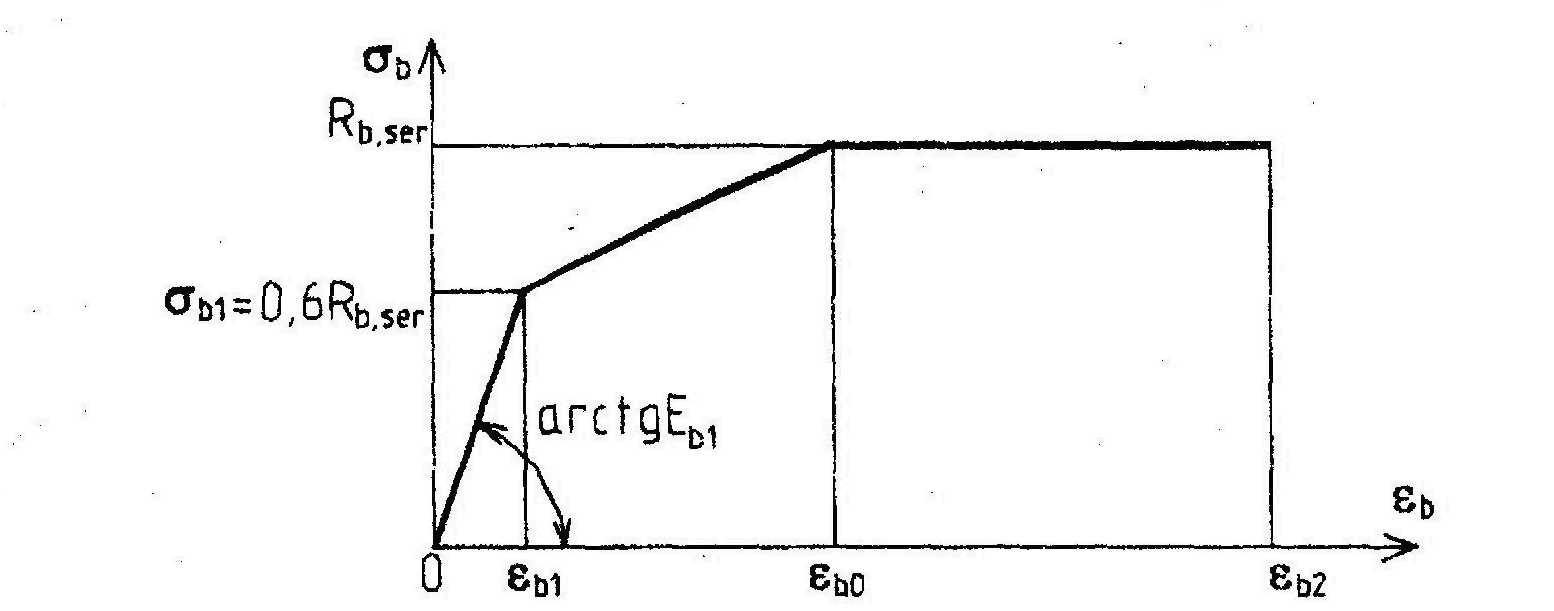
Черт.4.11. Трехлинейная диаграмма состояния сжатого бетона при расчетах по 2-й группе предельных состояний

Определение углов сдвига железобетонного элемента

4.26. Угол деформации сдвига определяется по формуле

(4.43)

где Q_x - поперечная сила в сечении х от действия внешней нагрузки;

G - модуль сдвига бетона (см. п.2.10);

φ_b- коэффициент, учитывающий влияние ползучести бетона и принимаемый равным: при продолжительном действии нагрузок - φ_b = 1 + φ_b,cr, где φ_b,cr - см. табл. 2.6 п. 2.9; при непродолжительном действии нагрузки φ_b =1,0;

φ_crc - коэффициент, учитывающий влияние трещин на деформации сдвига и принимаемый равным:

- на участках по длине элемента, где отсутствуют нормальные и наклонные к продольной оси элемента трещины, - φ_crc = 1,0;

- на участках, где имеются только наклонные трещины, - φ_crc = 4,0;

- на участках, где имеются только нормальные или нормальные и наклонные трещины, коэффициент φ_crc определяется по формуле

(4.44)

где М_x и - соответственно момент и кривизна от внешней нагрузки при непродолжительном ее действии;

I_red - момент инерции полного приведенного сечения при коэффициенте приведения арматуры к бетону a = E_s/E_b.

Отсутствие наклонных трещин соответствует выполнению условия (3.71) п.3.40