22.Расчёт центрально растянутых элементов.

Как правило, нижние пояса ферм, затяжки арок, некоторые стержни деревянных сквозных конструкций. Деревянные элементы работают на центральное напряжение рассчитывают по наиболее растянутому сечению: δ_р=N/F_нт≤R_р×m_о, где

F_нт – площадь сечения (нетто); m_о=0,8 – учитывает концентрацию напряжений, которая возникает в месте ослаблений.

Древесина работает на растяжение почти как упругий материал и имеет высокую прочность. Разрушения растянутых элементов происходит хрупко в виде почти мгновенно разрыва наименее прочных волокон по пилообразной поверхности. При наличии ослаблений, в пределах длины 20 см. в разных сечениях поверхность разрыва всегда проходит через них. При определении ослабленной площади сечения F_нт все оснащения на этой длине суммируются и как бы совмещаются в одном сечении.

23.Расчёт центрально сжатых элементов цельного сечения.

На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм и др. сквозные конструкции. Древесина работает на сжатие более надёжно, чем на растяжение, но не вполне упруго. Здесь пластические свойства древесины проявляются значительно сильнее, чем при растяжении. В данном случае пороки реальной древесины меньше снижают прочность сжатых элементов, поскольку сами воспринимают часть сжимающих напряжений. В растянутых элементах пороки выключаются из работы моментально. Вследствие, этого сжатые элементы рекомендуется изготавливать, как правило, из более доступной древесины 2 сорта.

Расчёт центрально сжатых элементов на прочность следует производить по формуле: δ_с=N/F_нт≤R_с,

В основном расчёт на прочность необходим для коротких стержней, у которых длина ≤ 7 толщин. Более длинные элементы, не закреплённые в поперечном направлении связями следует рассчитывать продольный изгиб, который состоит в потере гибким центрально сжатым прямым стержнем своей прямолинейной формы, что называется потерей устойчивости. Потеря устойчивости происходит раньше, чем напряжение сжатия достигнет придела прочности. При потере устойчивости несущий элемент теряет несущую способность и выгибается в сторону. При дальнейшем выгибе на вогнутой стороне появляются складки, свидетельствующие о разрушении от сжатия, а их выпуклая разрушается от растяжения.

На устойчивость ведут расчёт по формуле: δ_с=N/(φ×F_расч)≤R_с, δ_с=N/ F_расч≤ φ×R_с,

Прочность стержня при сжатии и потери устойчивости зависят от площади F_расч и формы его сечения, длины l и также закрепления концов стержня, что учитывается коэффициентом устойчивости или коэффициентом продольного изгиба (φ),

А) ослабление не выходит на кромку, т.е. располагаются в середине сечения. При отсутствии ослаблений или ослаблений в опасных сечениях не выходящих на кромку, если площадь ослабления не превышает 25% полного сечения F_бр, то F_расч = F_бр,

Б)При ослаблении не выходящих на кромки, если площадь ослабления превышает 25% F_бр, то:

F_расч = 4/3×F_нт ,

В) Симметричное ослабления, выходящие на кромки, то: F_расч = F_нт .

Коэффициент продольного изгиба (φ)элемента определяется в зависимости от его расчётной длины l₀, радиуса инерции r,таким образом зависит от гибкости элементов: λ= l₀/r;

В общем случае коэф. продольного изгиба можно найти следующим образом: φ=δ_кр/R^вр_с;

Т.е устойчивость определяется критическим напряжением δ_кр.

δ_кр=N_кр/F , теоретическое значение критической нагрузки для абсолютно упругого стержня было определено Эйлером: N_кр =Π×Е×У/ l²₀ ;

l₀- расчётная длина, которая учитывает влияние типа закрепления концов стержня на устойчивость.

Вообще критическая сила – это максимальная сила способная удержать стержень в искривлённом состоянии при котором может быть раздвоение оси стержня (1 критическая сила).

; ; следовательно , при λ>70.

то для древесины будет равно А=3000, для фанеры А=2500,

при λ>70

Формула Эйлера справедлива только в тех случаях, когда стержень теряет устойчивость при напряжении ≤ пределу пропорциональности, когда модуль упругости постоянен. Е=const и придел материала так же постоянен.

Если построить кривую Эйлера, то будет видно, что при малых гибкостях, когда критическое напряжение превышает предел пропорциональности, коэффициент продольного изгиба получается больше 1, чего по существу быть не может. Поэтому

при λ≤70 то

Эта формула получена опытным путём, соответствует работе стержня за пределом пропорциональности, когда меняется модуль упругости (Е≠const), а=0,8 – для древесины, а=1 – для фанеры.

Если l₀/h≤7, то φ≈1,

Гибкость зависит от радиуса инерции сечения ; , для прямоугольного сечения

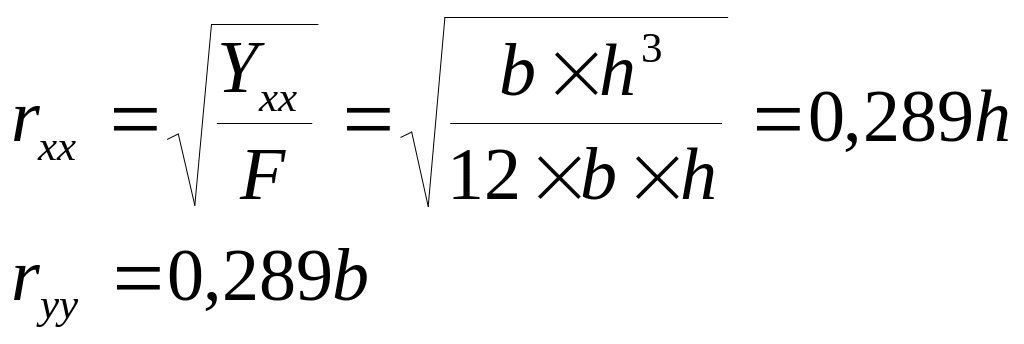
для круглого сечения ;

Гибкость λ сжатых элементов ограничивается с тем, чтобы они получились недопустимо неустойчивыми и недостаточно надёжными. Поэтому гибкость элемента ограничивают, например:

-отдельные стойки, верхние пояса ферм, опорные раскосы ферм λ≤[λ]=120

-прочие сжатые элементы основных несущих конструкций λ≤150

-сжатые элементы связей λ≤200