30. Линии и поверхности уровня.

31. Предел функции нескольких переменных.

Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Множество всех точек М(х;у) плоскости, координаты которых удовлетворяют неравенству , называется δ-окрестностью точки М₀(х₀;у₀). Другими словами, δ - окрестность точки М₀ - это все внутренние точки круга с центром М₀ и радиусом δ (см. рис.2).

Пусть функция u=f(x;y) определена в некоторой окрестности точки М₀(х₀;у₀), кроме, быть может, самой этой точки. Число А называется пределом функции u=f(x;y) при х → x₀ и у → y₀ (или, что то же самое, при М(х;у) → М₀(х₀;у₀)), если для любого ε>0 существует такое δ>0, что для всех х ≠ х₀ и у ≠ у₀ и удовлетворяющих неравенству выполняется неравенство < ε. Записывают: или

Из данного определения следует, что если предел существует, то он не зависит от пути, по которому М стремится к М₀ (число таких направлений бесконечно; для функции же одной переменной х → х₀ только по двум направлениям: слева и справа!)

Геометрический смысл предела функции двух переменных состоит в следующем. Каково бы ни было число ε > 0, найдется δ-окрестность точки M₀(x₀;y₀), что во всех ее точках М(х;у), отличных от М₀, аппликаты соответствующих точек поверхности u=f(x;y) отличаются от числа А по модулю меньше, чем на ε.

32. Частные производные. Полный дифференциал.

Частные производные. Пусть  - функция двух переменных, определенная в некоторой окрестности точки . Если существует конечный предел   , то говорят, что функция   имеет в точке частную производную по переменной  . Аналогично определяется частная производная по   . Обозначают:

.

Пусть - функция n переменных, определенная в области  n-мерного пространства. Частной производной функции по переменной называется предел

.

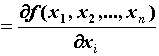Из определения частной производной следует правило: при вычислении производной по одной из переменных все остальные переменные считаем постоянными, учитывая, что производная постоянной равна нулю и постоянную можно выносить за знак производной.

33. Производная по направлению.

производная по направлению. Если в n-мерном пространстве задан единичный вектор , то изменение дифференцируемой функции в направлении этого вектора характеризуется производной по направлению: . В частности, для функции трех переменных 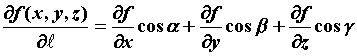 ,  - направляющие косинусы вектора  .

34. Градиент.

Градиент. Производная по направлению представляет собой скалярное произведение вектора  и вектора с координатами  , который называется градиентом функции   и обозначается    . Поскольку  , где  - угол между   и  , то вектор указывает направление скорейшего возрастания функции   , а его модуль равен производной по этому направлению.

35. Производные и дифференциалы высших порядков.

Производные и дифференциалы высших порядков. Дифференцируя частную производную как функцию нескольких переменных по одной из переменных, получим производные второго порядка. Например, для функции двух переменных: . Если смешанные производные     и     непрерывны, то они равны, то есть не зависят от порядка дифференцирования. Аналогично определяются, например,    . Если при вычислении полного дифференциала от дифференциала первого порядка учесть, что приращения аргументов есть числа и оставить их неизменными, то получим дифференциал второго порядка. Например, для функции двух переменных:   . Здесь учтено равенство смешанных производных второго порядка и принято   . При этих допущениях формулу дифференциала любого порядка можно получить из символического выражения:   .