48. Извлечение корней из комплексного числа.

Заголовок этого раздела является не совсем точным. Дело в том, что корень из ненулевого комплексного числа однозначно определить нельзя. Он всегда имеет столько значений, какова его степень. Поэтому в данном разделе мы будем говорить о решении уравнения

(17.14)

где неизвестным служит , а  -- известное комплексное число. Но поскольку в школе решение этого уравнения записывалось в виде , то, не слишком соблюдая математическую строгость, можно говорить, что мы будем извлекать корень -ой степени из комплексного числа . Итак, решаем уравнение (17.14).

Если , то . Пусть . Запишем число в тригонометрической форме: . Здесь и  -- известные величины. Запишем неизвестное число в тригонометрической форме: . Здесь и  -- неизвестны. По формуле Муавра

Таким образом,

Если два комплексных числа равны, то их модули должны быть равны. Поэтому . В этом соотношении и  -- положительные числа, следовательно , где справа стоит обычный арифметический корень из положительного числа.

Если два комплексных числа равны, то аргументы у них могут различаться только на величину, кратную . Поэтому , . Отсюда находим, что

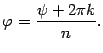
В итоге получили:

Значения , отличные от указанных в этой формуле, дадут те же значения , которые можно получить при