Построение и расчет параметров сетевых графиков

Изучение данного вопроса рассмотрим на примере последовательности работ, приведенной в таблице 1.1. Сначала построим сетевой график.

Таблица 1.1

Последовательность работ
Исходная работа	Опирается на работу	Продолжительность работ
а1	-	3
a2	-	6
a3	-	4
a4	а1	5
a5	a2	1
a6	a3	9
a7	a3, a5,	6
a8	a4, a6 ,a7	8

Работы а1,а2 и а3 не имеют предшествующих, поэтому реализация проекту начинается с этих работ; они изображаются дугами, выходящими из одной вершины — события х1 Работе а4 предшествует работа а1, поэтому дуга а4 на сети изображена вслед за дугой а1. То же самое с дугами а5 и а6. Далее надо изобразить дуги а7 и а8. Работа а7 опирается на работы а3 и а5. Итоговая работа а8 опирается на а4, а6 и а7.Таким образом, сетевой график рассматриваемого примера имеет вид (рис.1.18). Если, к примеру, работа а5 опиралась бы еще на а1, то между событиями х2 и х3 пришлось бы ввести штриховую дугу.

Рис. 1.18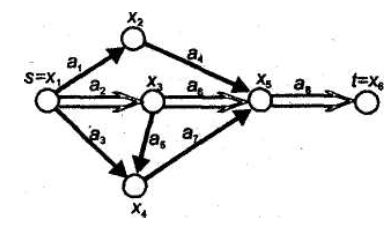

Основные параметры сетевых моделей- это критический путь, резервы времени событий, путей и работ. Кроме этих параметров имеется ряд вспомогательных, которые используются для получения дополнительных характеристик по анализу и оптимизации сетевого графика. Рассмотрим порядок определения параметров.

Имея сеть работ некоторого проекта, можно посчитать время выполнения всего проекта и различных его частей, состоящих из разного набора работ. Сначала введем несколько определений. Определим минимальное время, за которое можно выполнить все работы комплекса. Для этого найдем про- должительность t(μi) всех полных путей μi. Полный путь – это любой путь, начало которого совпадает с исходным событием сети, а конец-с завершающим. В нашем случае таких путей четыре: μ1 : x1-x2-x5-x6; μ2 : x1-x3-x5-x6; μ3 : x1-x4-x5-x6; μ4 : x1-x3-x4-x5-x6.

Их продолжительности в днях составляют: t(μ1)=16, t(μ2)=23, t(μ3)=18, t(μ4)= 21. Наиболее продолжителен второй путь, который называют критическим. Он определяет минимальное время выполнения всех работ комплекса. Минимальное время называют критическим сроком и обозначают tкр. Итак, в рассматриваемом примере tкp =23 дня. Все работы и события, лежащие на критическом пути, называют критическими, все остальные работы и события — некритическими.

Задержка любой критической работы вызывает задержку выполнения всего комплекса. Следовательно, чтобы уменьшить время выполнения комплекса работ, надо сократить сроки критических работ. Некритические работы допускают некоторое запаздывание их выполнения без нарушения критического срока. Это запаздывание измеряется резервом времени событий и работ.

Свершением события называется момент, к которому заканчиваются все входящие в него работы, и может быть начата любая выходящая работа.

Некоторые события можно совершать в разные моменты, т.е. варьировать свершение этих событий. Например, событие х2 может свершиться через три дня (по окончании работы a1), но может наступить и позже на срок до семи дней, поскольку на пути μ1, где лежит это событие, есть резерв времени tкр-t(μ1)= 23 -16 = 7 дней. Поэтому для событий различают ранний и поздний сроки свершения.

Ранним сроком tр(xj) свершения события xj называется самый ранний момент времени, к которому завершатся все работы, предшествующие этому событию. Ранние сроки для всех событий могут быть рассчитаны по формуле tр(xj)=max(tр(xi)+t(xi,xj)) (1.9) (xi,xj)ЄU+j

где U+j — множество работ, входящих в xj событие; tр(xi)— ранний срок свершения начального события работы(xi,xj); t(xi,xj)—продолжительность работы (xi,xj)

Поздним сроком tп(xi) свершения события xi называется самый поздний момент времени, после которого остается ровно столько времени, сколько необходимо для завершения всех работ, следующих за этим событием. В нашем случае tп(x6)=23. Чтобы не нарушался критический срок, событие x5 должно произойти, в крайнем случае, на восемь дней раньше, поэтому

tп(x5)=23-8=15.

tп(xj)=min(tп(xj)- t(xi,xj)), (1.10)

(xi,xj)ЄU -i

где Ui-множество работ, выходящих из xi события, tп(xj)-поздний срок свершения

конечного события работы (xi,xj).

Разность между поздним и ранним сроками свершения события xt составляет резерв времени R(xi) этого события:

R(xi)=tп(xi)-tр(xi). (1.11)

Резерв показывает, на какой предельно допустимый срок может задержаться свершение события xi без изменения срока наступления итогового события z=x6. У критических событий ранние и поздние сроки совершения совпадают, ибо резерв времени у них равен нулю.

Зная сроки свершения событий, можно найти ранние и поздние сроки начала и окончания работы (xi,xj), Очевидно, что

t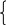 р.н (xi,xj)=tр(xi), tр.о (xi,xj)=tр(xi)+ t(xi,xj),

tп.о (xi,xj)=tп(xi), tп.н (xi,xj)=tп(xj)-t(xi,xj), (1.12)

Прежде чем рассматривать резервы времени работ, обратимся к резерву времени пути. Такие резервы имеют все некритические пути. Резерв времени пути R(μi) определяется как разность между длиной критического и рассматриваемого пути

R(μi)= tкр-t(μi). (1.13)

Он показывает, на сколько в сумме могут быть увеличены про- должительности всех работ, принадлежащих этому пути. Если затянуть выполнение работ, лежащих на этом пути, на время большее чем R(μi), то критический путь переместится на путь μi.

Отсюда можно сделать вывод, что любая из работ пути μi на его участке, не совпадающем с критическим путем (замкнутым между двумя событиями критического пути), обладает резервом времени. Среди резервов времени работ выделяют четыре разновидности.

Полный резерв времени Rп(xi,xj) работы (xi,xj) показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Полный резерв Rп(xi,xj) определяется по формуле

Rп(xi,xj) = tп(xj)- tр(xi)- t(xi,xj). (1.14)

Полный резерв времени работы равен резерву максимального из путей, проходящего через данную работу. Этим резервом можно располагать при выполнении данной работы, если ее начальное событие свершится в самый ранний срок, и можно допустить свершение конечного события в его самый

поздний срок (рис.1.19а).

Важным свойством полного резерва времени работы является то, что он принадлежит не только этой работе, но и всем полным путям, проходящим через нее. При использовании полного резерва времени только для одной работы резервы времени остальных работ, лежащих на максимальном пути, проходящем через нее, будут полностью исчерпаны. Резервы времени работ, лежащих на других (не максимальных по длительности) путях, проходящих через эту работу, сократятся соответственно на величину использованного резерва.

Остальные резервы времени работы являются частями ее полного резерва.

31