Одноканальная смо с неограниченной очередью и её характеристики.

В качестве показателей эффективности СМО с ожиданием, кроме показателей абсолютной А и относительной Q пропускной способности, вероятности отказа Ротк, среднего числа занятых каналов κ (дл многоканальной системы), будем рассматривать также следующие:

Lcucm – среднее число заявок в системе;

Тсист – среднее время пребывания заявки в системе;

Lоч – среднее число заявок в очереди (длина очереди);

Точ – среднее время пребывания заявки в очереди;

Рзан – вероятность того, что канал занят (степень загрузки канала).

На практике часто встречаются одноканальные системы с неограниченной очередью (например, телефон-автомат). Рассмотрим следующую задачу. Имеется одноканальная СМО с очередью, на которую не наложены никакие ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок, поступающий в СМО, имеет интенсивность λ, а поток обслуживания – интенсивность μ . Необходимо найти предельные вероятности состояний и показатели эффективности СМО.

Система может находиться в одном из состояний S0, S1, S2,..., Sk по числу заявок, находящихся в СМО: S0 – канал свободен, S1 – канал занят (обслуживает заявку), очереди нет, S2 – канал занят, одна заявка стоит в очереди, ..., Sk – канал занят, (k – 1) заявка стоит очереди и т.д. Граф состояний СМО представлен на рис. 7.

Рис. 7. Граф состояний одноканальной системы с неограниченной очередью

Это процесс гибели и размножения, но с бесконечным числом состояний, в котором интенсивность потока заявок равна λ, а интенсивность потока обслуживания μ . Пусть ρ есть отношение среднего числа приходящих заявок к среднему числу обслуживаемых заявок (в единицу времени).

Доказано следующее утверждение: если ρ < 1, то предельные вероятности существуют; если ρ > 1, то очередь растет до бесконечности.

Для определения предельных вероятностей состояний применим формулы

(29), (30) для процесса размножения и гибели:

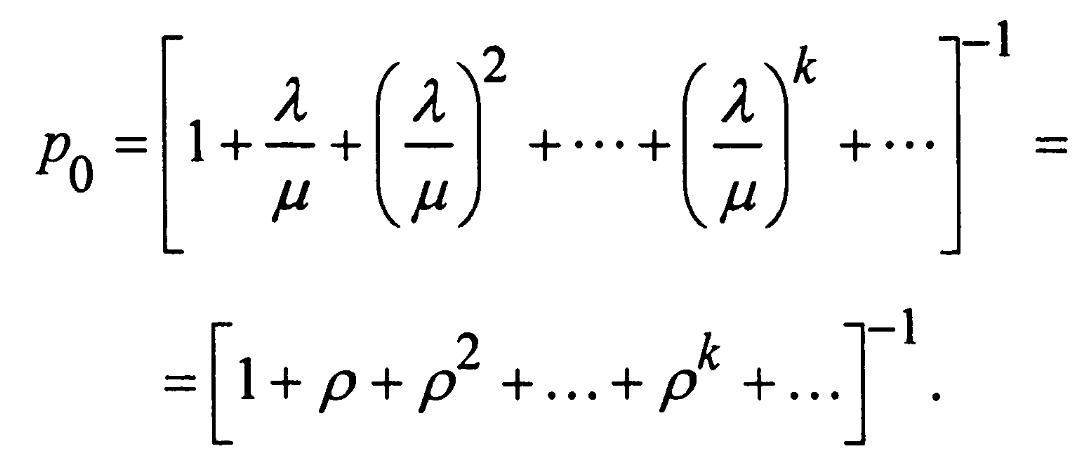(38)

Так как предельные вероятности существуют только при ρ < 1, то геометрический ряд со знаменателем ρ < 1, записанный в скобках в формуле (38), сходится к сумме, равной 1/1 – ρ

Поэтому p₀ = 1 – p . (39)

С учетом (30) p1 = ρ p0; p2 = ρ2 p0; …

Найдем предельные вероятности других состояний:

p1 = ρ (1 – ρ); p2 = ρ2 (1 – ρ); …, pk = ρk (1 – ρ). (40) Предельные вероятности р0, р1, р2,..., рk,... образуют убывающую геометрическую прогрессию со знаменателем ρ < 1, следовательно, вероятность p0 – наибольшая. Это означает, что если СМО справляется с потоком заявок (при ρ < 1), то наиболее вероятным будет отсутствие заявок в системе.

Среднее число заявок в системе L_сист определим по формуле

математического ожидания, которая с учетом (40) примет вид

(41)

Можно показать, что формула (41) преобразуется (при ρ < 1) к виду

Lсист = ρ/1 – ρ (42)

Найдем среднее число заявок в очереди Lоч. Очевидно, что

L_оч = L_сист – L_{об , (43)}

где L_об – среднее число заявок, находящихся под обслуживанием. Среднее число заявок под обслуживанием определим по формуле математического ожидания числа заявок под обслуживанием, принимающей значение 0 (если канал свободен) либо 1 (если канал занят):

Lоб = 0 · p0 + 1(1 – p0), т.е. среднее число заявок под обслуживаем равно вероятности того, что канал

занят:

Lоб = Рзан = 1 – p0. (44)

В силу того, что p₀ = 1 – ρ получим:

Lоб = Рзан = ρ.

Далее по формуле (43) с учетом (42) и (44) получим

Lоч = ρ²/1 – ρ

Доказаны следующие утверждения: при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе (очереди) равно среднему числу заявок в системе (очереди), деленному на интенсивность потока заявок, т.е

Тсист = 1/ λ Lсист , (46)

Точ = 1/ λ Lоч (47)

Формулы (46) и (47) называются формулами Литтла. Они вытекают из того, что в предельном стационарном режиме среднее число заявок, прибывающих в систему, равно среднему числу заявок, покидающих ее: оба потока заявок имеют одну и ту же интенсивность λ.

На основании (46) и (47) с учетом (40) и (44) среднее время пребывания

заявки в системе определяется по формуле

Тсист =ρ/λ(1 – ρ) (48)

а среднее время пребывания заявки в очереди

Точ = ρ²/λ (1 – ρ)

Многоканальная СМО с ограниченной длиной очереди и её характеристики.

Показатели обслуживания многоканальной СМО с ограниченной очередью

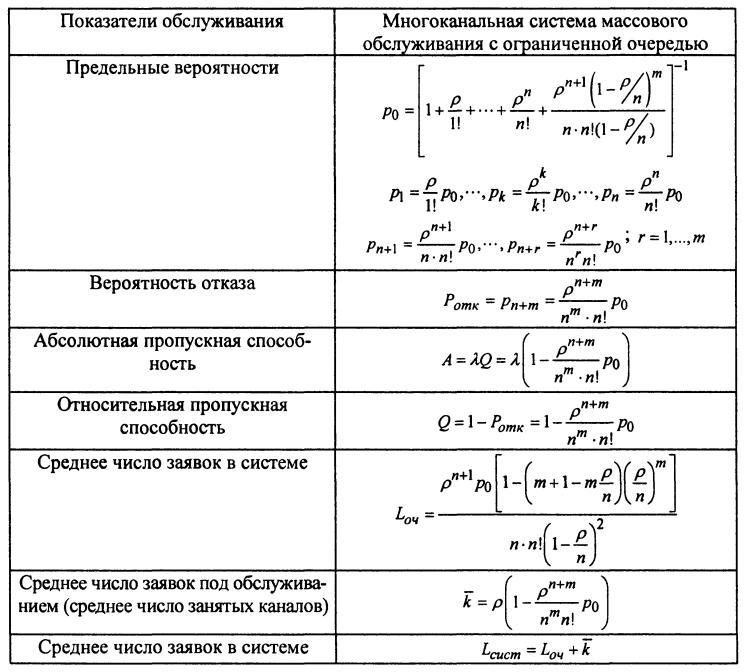
Многоканальная СМО с неограниченной очередью и её характеристики

Рассмотрим следующую задачу. Имеется n-канальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживания – интенсивность μ. Необходимо найти предельные вероятности состояний СМО и показатели ее эффективности.

Система может находиться в одном из состояний S0, S1, S2,..., Sk,…, Sn..., нумеруемых по числу заявок, находящихся в СМО: S0 – в системе нет заявок (все каналы свободны), S1 – канал занят, S2 – заняты два канала, остальные свободны, ..., Sk – занято k каналов, остальные свободны, ..., Sn – заняты все n каналов (очереди нет); Sn + r – заняты все n каналов, r заявок в очереди.

Рассмотрим граф состояний этой системы (рис. 8). Отметим, что в отличие от предыдущей ситуации, интенсивность потока обслуживания (переводящего систему из одного состояния в другое справа налево) не остается постоянной, а по мере увеличения числа заявок в

СМО от 0 до n увеличивается от величины μ до величины n μ, так как соответственно увеличивается число каналов обслуживания. Когда число заявок в системе больше n, интенсивность потока обслуживания сохраняетсяравной n μ.

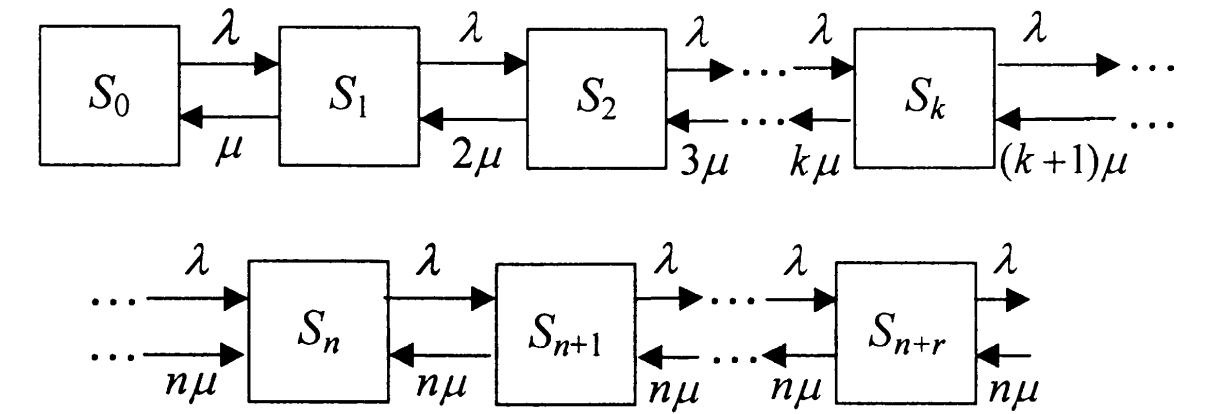
Рис. 8. Граф состояний многоканальной системы с неограниченной очередью

Можно доказать, что если отношение ρ / n < 1, предельные вероятности существуют. В том случае, когда ρ / n ≥ 1, очередь неограниченно растет.

Используя формулы (21), (22) для процесса размножения и гибели, получим формулы для предельных вероятностей состояний n-канальной СМО с неограниченной очередью. 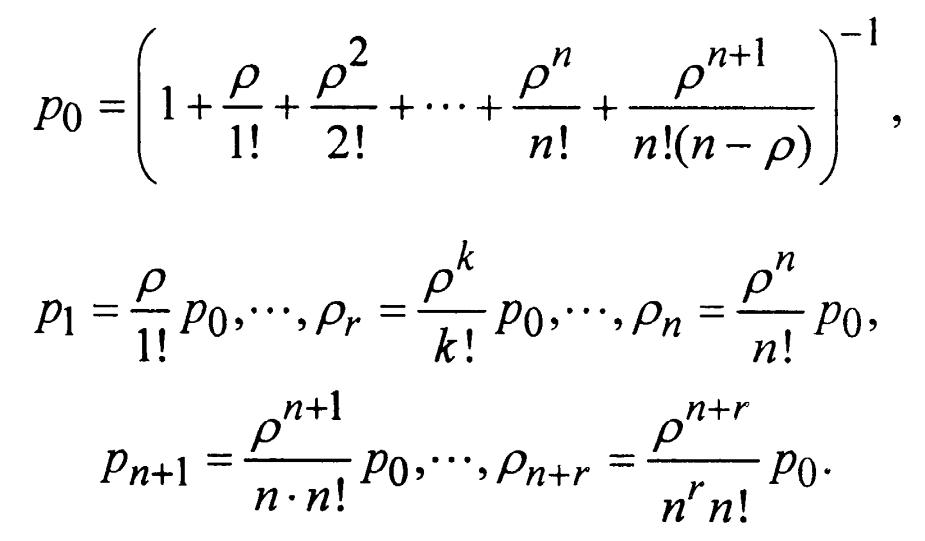(50), (51),(52)

Вероятность того, что заявка окажется в очереди (53)

Для n-канальной СМО с неограниченной очередью, используя прежние приемы, можно найти:

а) среднее число занятых каналов (54)

б) среднее число заявок в очереди 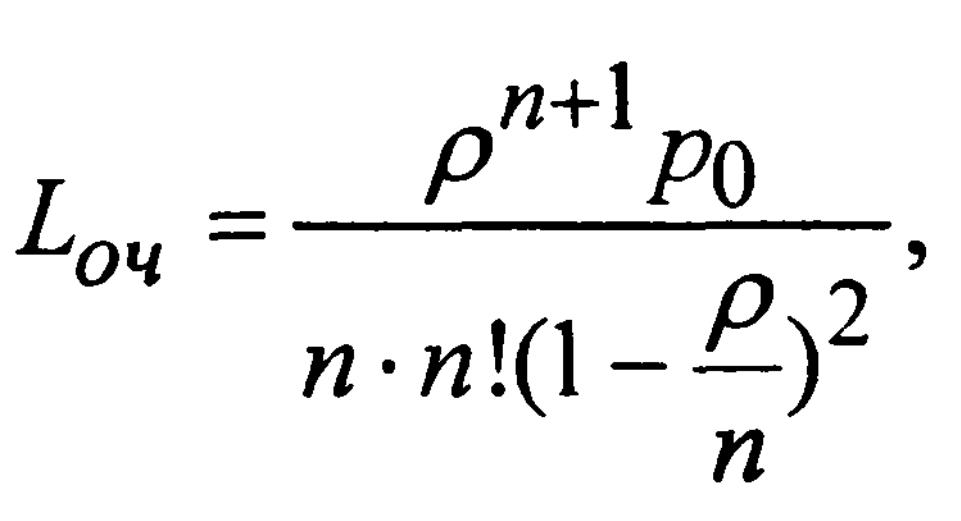(55)

в) среднее число заявок в системе

Lсист = Lоч + ρ . (56)

Среднее время пребывания заявки в очереди и среднее время пребывания заявки в системе вычисляются по формулам Литтла (47) и (48).

Отметим, что для систем с неограниченной очередью при ρ < 1 любая заявка, пришедшая в систему, будет обслужена, т.е. вероятность отказа

Ротк = 0, относительная пропускная способность Q = 1, а абсолютная пропускная способность равна интенсивности входящего потока заявок, т.е. А = λ .

Сетевое планирование. Правила построения сетевых моделей. Параметры построения сетевых моделей (ранний/поздний срок свершения j-го события, ранний срок начала/окончания работы, поздний срок начала/окончания работы, полный резерв времени работы, полный резерв времени пути). Методы расчета параметров сетевых моделей.

Сетевое планирование в таможенном деле

Сетевое планирование основано на моделировании процесса с помощью сетевого графика и представляет собой совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ.

Первые системы, использующие сетевые графики, были применены в CША в конце 50-х годов и получили название СРМ (английская аббревиатура, означающая метод критического пути) и PERT(метод оценки и обзора программы). Система СРМ была впервые применена при управлении строительными работами, система PERT- при разработке ракетной системы «Поларис».

Под комплексом работ понимается всякая задача, для выполнения которой необходимо осуществить достаточно большое количество разнообразных работ. Это может быть строительство здания или любого другого сложного объекта, разработка проекта сооружения, работа таможенного поста и т.д.

Для того чтобы составить план работ, состоящих из множества отдельных исследований и операций, необходимо описать его с помощью некоторой математической модели. Таким средством описания проектов, комплексов и т.д. является сетевая модель.