35.Одноканальная модель смо с отказами в обслуживании и её характеристики

В качестве показателей эффективности СМО с отказами будем рассматривать:

А – абсолютную пропускную способность СМО, т.е. среднее число заявок, обслуживаемых в единицу времени.

Q – относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;

Ротк – вероятность отказа, т.е. того, что заявка покинет СМО необслуженной;

κ – среднее число занятых каналов (для многоканальной системы). Рассмотрим одноканальную систему с отказами.

Пусть имеется один канал, на который поступает поток заявок с интенсивностью λ. Поток обслуживания имеет интенсивность μ. Найти предельные вероятности состояний системы и показатели ее эффективности.

Система S имеет два состояния:

а) S0 – канал свободен;

б) S1 – канал занят.

Размеченный граф состояний представлен на рис. 5.

Рис. 5. Граф состояний одноканальной системы с отказами

В предельном стационарном режиме система алгебраических уравнений для вероятностей состояний имеет вид:

λ p0 = μ p1 (31)

μ p1 = λ p0

Заметим, что система вырождается в одно уравнение. Учитывая, что

p0 + p1 = 1, найдем из (31) предельные вероятности состояний

p0 = μ/λ + μ; p1 = λ/λ + μ ,

которые выражают среднее относительное время пребывания системы в состоянии S0 (когда канал свободен) и S1 (когда канал занят), т.е. определяют соответственно пропускную способность Q системы и вероятность отказа Ротк.

Q = μ/μ + λ (32)

Ротк = λ/λ + μ (33)

Абсолютную пропускную способность найдем, умножив относительную пропускную способность на интенсивность потока отказов: A = λ μ/λ + μ

Многоканальная СМО с отказами в обслуживании и её характеристики.

Рассмотрим классическую задачу Эрланга. Имеются n каналов, на которые поступает поток заявок интенсивности λ. Поток обслуживания имеет интенсивность μ. Найти предельные вероятности состояний системы и показатели ее эффективности.

Система S имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): S0, S1, S2,..., Sk,..., Sn . Здесь Sk – состояние системы, когда в ней находится k заявок, т.е. занято k каналов.

Граф состояний СМО, соответствующий процессу гибели и размножения на рис. 6.

Рис. 6. Граф состояний задачи Эрланга

Поток заявок переводит систему из любого левого состояния в соседнее правое состояние. Интенсивность потока обслуживания, наоборот, переводит систему из любого правого состояния в соседнее левое состояние.

Действительно, если СМО находится в состоянии S2 (два канала заняты), то она может перейти в состояние S1 (один канал занят), когда либо первый, либо второй канал закончат обслуживание. Аналогично для любого из состояний S₃,...,S_n .

Для этой задачи в стационарном режиме Эрлангом были найдены следующие зависимости: (начало то же, что и в одноканальной СМО см 35 +..)

1. Вероятность того, что обслуживанием заняты k каналов:

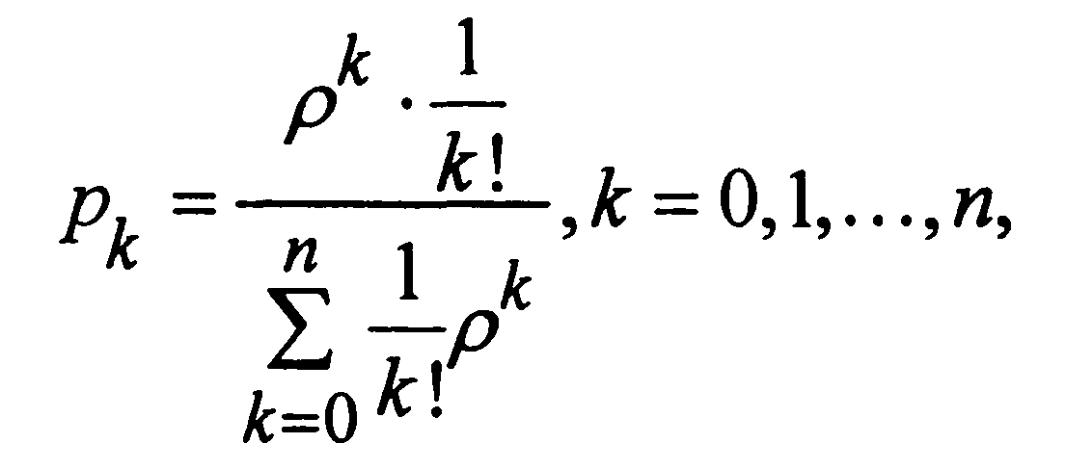(35)

где ρ^k = λ/μ; λ – плотность потока заявок

n – число каналов (приборов);

μ = 1 / t_обс – параметр обслуживания одним прибором (каналом).

2. Частными случаями (35) являются:

а) вероятность того, что все обслуживающие приборы свободны

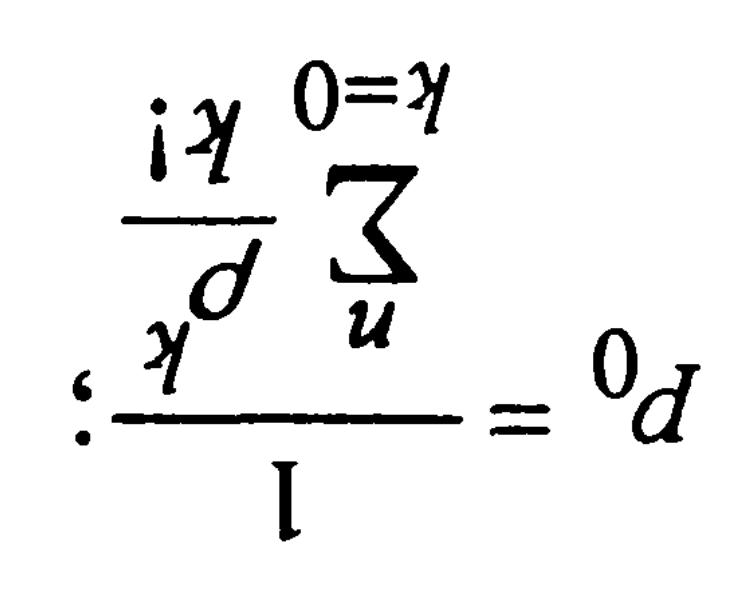
б) вероятность того, что все приборы заняты. Это одновременно и вероятность отказа в обслуживании вновь поступившего требования в систему

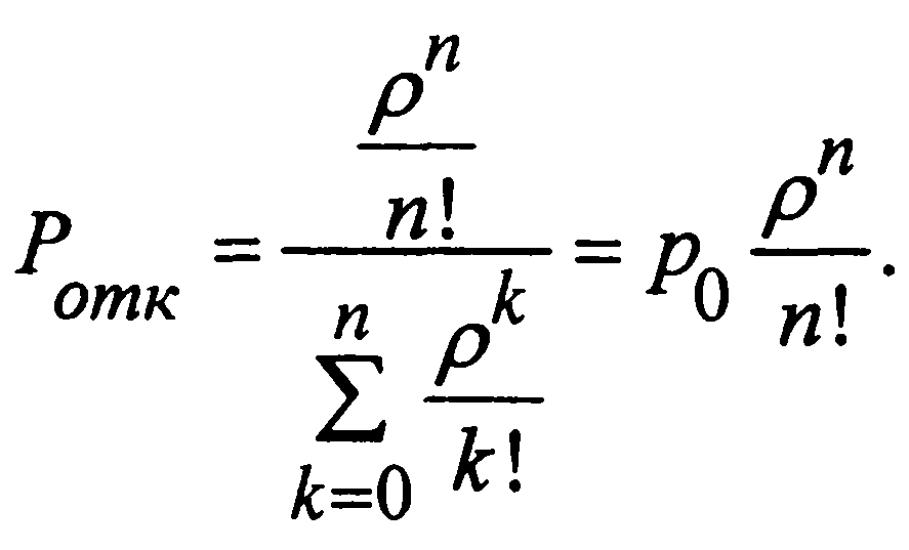
3. Среднее число приборов, занятых обслуживанием

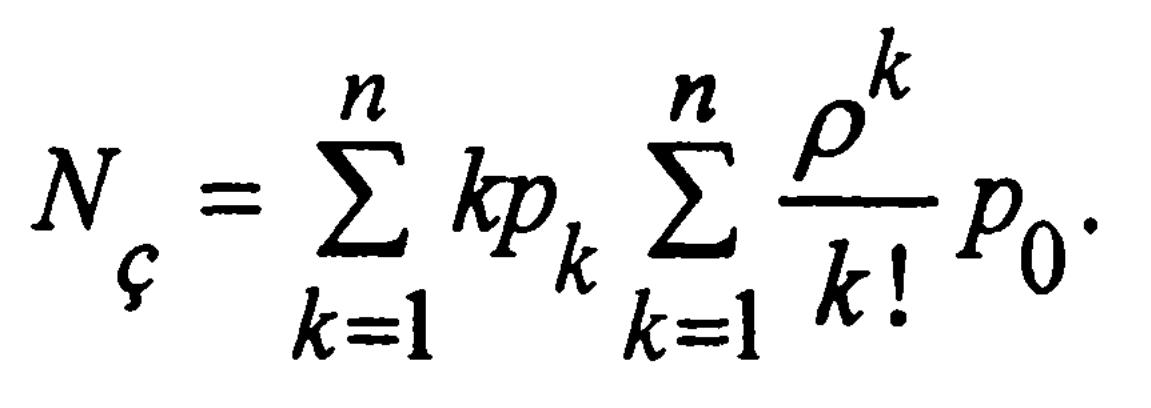
4. Коэффициент загрузки приборов

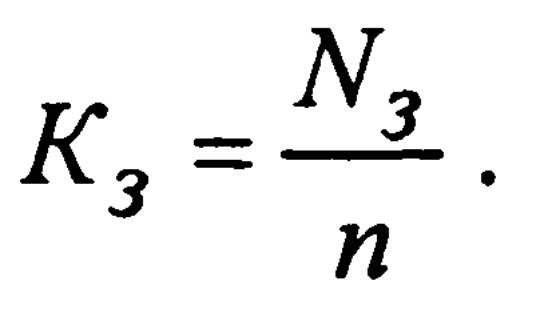
5. Среднее число каналов, свободных от обслуживания

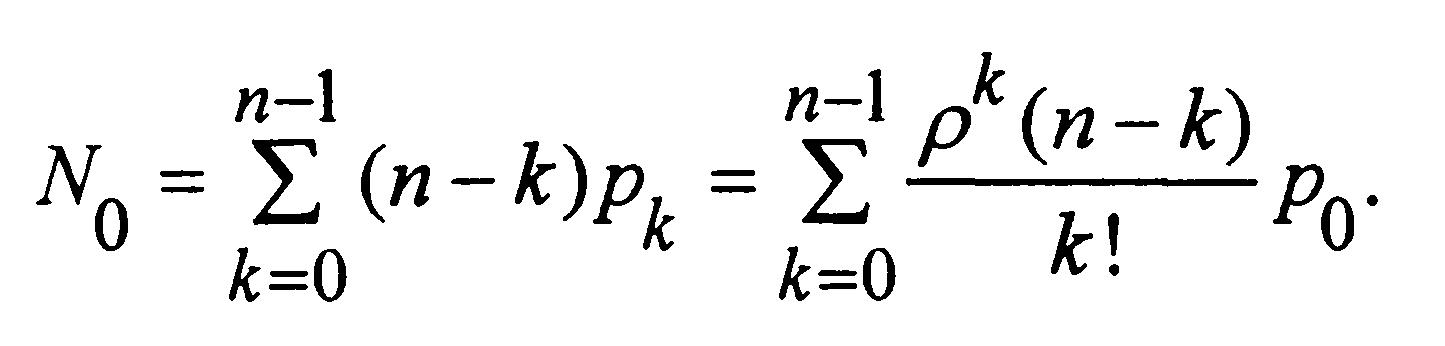
6. Коэффициент простоя каналов

Очевидно, что N₃ + N₀ = n. Несмотря на то, что эти зависимости выведены при условии, что время обслуживания распределено экспоненциально, другими исследователями доказана справедливость формул Эрланга для произвольного непрерывного закона распределения обслуживания (при условии конечности его математического ожидания). Эти выводы позволяют значительно расширить рамки применимости формул Эрланга.

Одноканальная СМО с ограниченной длиной очереди и её характеристики(+ следующий)

СМО с ограниченной очередью отличаются от рассмотренных лишь тем, что число заявок в очереди ограниченно, т.е. не может превосходить некоторого числа т . Если в очередь поступает т + 1 заявка, она покидаетсистему необслуженной, т.е. получает отказ.

Для вычисления предельных вероятностей состояний и показателей эффективности таких СМО может быть использован уже показанный подход.

Разница заключается в том, что суммировать надо не бесконечную прогрессию, а конечную. Среднее время пребывания заявки в очереди и в системе, как и ранее, определим по формулам Литтла (49), (48).

В условиях задачи о разгрузке судов определим показатели эффективности работы причала. Известно, что приходящее судно покидает причал (без разгрузки), если в очередь на разгрузку стоит более 3-х судов.

Решение. По условию т = 3. Используем формулы, приведенные в табл. 2.

Таблица2 Показатели обслуживания одноканальной СМО с ограниченной очередью