Корреляционная обработка сигнала

Говоря об корреляционной обработке сигнала, рассмотрим деятельность детектора (Рис.3). Удобно рассмотреть векторное представление сигналов и шума. Как мы уже упоминали реально в физической среде распространяются гармонические колебания некоторой амплитуды на наборе частот. Причем, как известно, при разложении в ряд Фурье, частоты выбираются так, что набор функций {cos(l_i * t)}, i=1..N, по которым раскладывают исходную функцию является ЛНЗ (линейно-независимым), т.е. образует базис в некотором N-мерном пространстве функций.

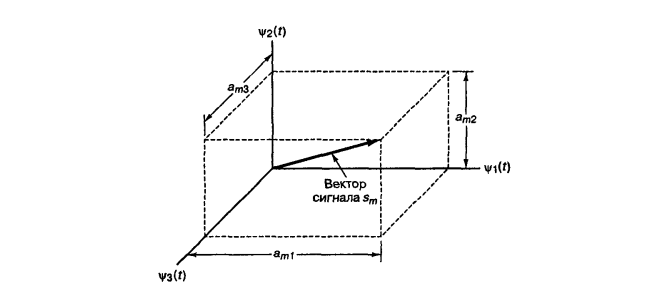
Рисунок 6. Векторное представление сигнала s_m(t)

Пусть N=3 и цифровой фильтр сделал измерение импульса s­_m(t). Тогда полученный сигнал можно представить в виде вектора в трёхмерном пространстве (см. Рис. 6). Модуль вектора при этом равен значению искомой функции. Казалось бы, на этом можно и остановиться – перебираем теперь набор сигналов-прототипов (как упоминалось выше, этот набор всегда конечен в цифровых системах) и детектируем тот, с которым полученный сигнал совпал. Но ведь реально полученный вектор будет отличаться от того, который предполагается получить (даже если мы хорошо поборолись с ISI с помощью выравнивающих фильтров, остаётся шум (здесь мы полагаем его AWGN)). Поэтому реально мы получаем кластер или облако векторов вокруг ожидаемых сигналов-прототипов (Рис. 7). Задача приёмника же состоит в том, чтобы решить, какой из прототипов сигнального пространства ближе к принятому вектору r.

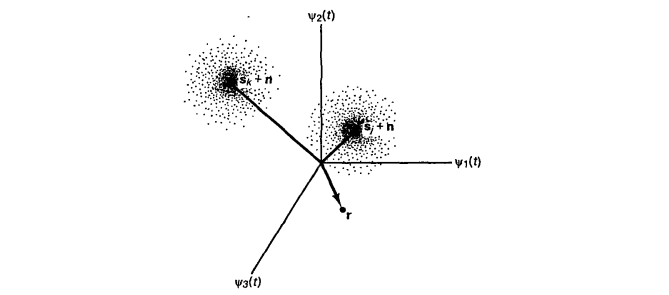
Рисунок 7. Сигналы и шум в трехмерном векторном пространстве

Здесь можно много рассуждать о выборе сигналов-прототипов так, чтобы минимизировать вероятность ошибки, но реальность в том, что наиболее эффективные решения появлялись независимо от этих рассуждений и являются интуитивно понятными. Поэтому массу громоздких формул мы здесь писать не будем, а лучше взглянем на пару способов кодирования сигналов и покажем детекторы, занимающиеся их корелляционной обработкой.

Униполярная передача сигналов

При униполярной передаче данных битовой 1-це соответствует значение A на всей протяженности одного символа T, а битовому 0-лю соответствует нулевое значение.

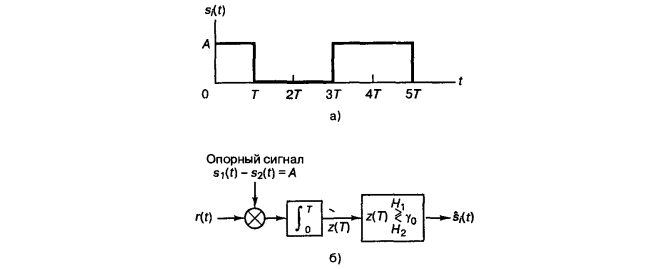
Рисунок 8. Детектирование при униполярной низкочастотной передаче сигналов

Детектор делает одно или несколько измерений за время T и, усредняя измерения (приближенное вычисление интеграла), сравнивает полученное значение с неким пороговым. Пороговое значение для каждого типа канала легко устанавливается практическим путём. Это позволяет избежать лишних пресуппозиций относительно характера шума и других.

Биполярная передача сигналов

При биполярной передаче данных битовой 1-це по-прежнему соответствует значение A на всей протяженности одного символа T, а битовому 0-лю соответствует значение -A.

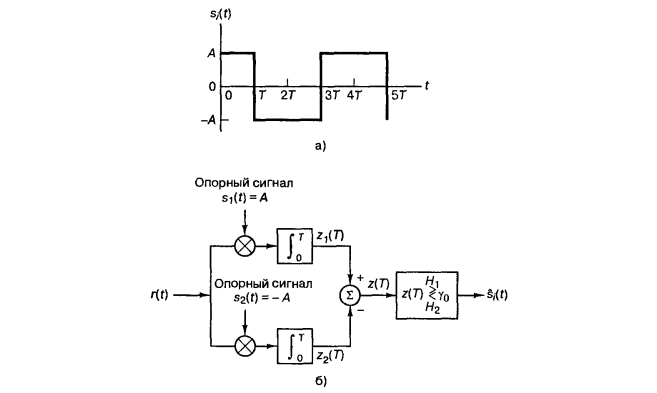
Рисунок 9. Детектирование при биполярной низкочастотной передаче сигналов

Этот вариант передачи сигналов более нагляден, поскольку показывает общую структуру корреляторов. Полученный сигнал проходит по k веткам, на каждой из которых сравнивается с опорным k-ым сигналом. И в результате выбирается тот из опорных, который лучше остальных кореллирует с полученным. Впрочем, не всегда детектор ограничивается этим. Часто принимающий фильтр может накапливать знания о близости векторов и принимать так называемые гибкие решения, как в уже упомянутом ранее алгоритме Витерби.