3.2 Выводы
На основании выполненного обзора распространенных методик расчета рам следует сделать ряд выводов:
1) Наиболее распространены режимы изгиба и кручения в расчете лонжеронных рам;
2) Предложенные методики часто не опираются на метод конечных элементов, а расчетные схемы, используемые в них, слишком просты;
3) Возникает необходимость разработки новых методик расчета, которые будут опираться не только на статические типы анализа.
4 Описание методики расчетов в конечно-элементных комплексах
В настоящее время область применения метода конечных элементов обширна и охватывает все физические задачи, которые могут быть описаны дифференциальными уравнениями. Наиболее важными преимуществами метода конечных элементов являются следующие [2]:
1) свойства материалов смежных элементов могут различаться;
2) криволинейная область может быть аппроксимирована или точно описана с помощью прямолинейных элементов;
3) размеры КЭ могут быть переменными;
4) возможно рассматривать граничные условия с разрывной поверхностной нагрузкой, а также смешанные граничные условия;
5) МКЭ может использоваться для составления общей программы для решения частных задач определенного класса.
Главный недостаток МКЭ заключается в необходимости составления программ и применения высокопроизводительных компьютерных средств, поскольку вычисления громоздки для ручного расчета даже при решении простых задач [36].
Сущность аппроксимации сплошной среды по методу конечных элементов (МКЭ) состоит в следующем: 1) домен сплошной среды с помощью воображаемых линий или поверхностей делится на поддомены конечных размеров (конечные элементы); семейство конечных элементов всего домена называется сеткой; 2) предполагается, что конечные элементы соединяются между собой в конечном числе точек, которые находятся на контуре элемента и называются узлами; 3) состояние в каждом элементе (например, поле перемещения, деформации, напряжения и др.) рассматривается с помощью интерполяционных функций и конечного числа параметров в узлах, представляющих основные неизвестные; 4) для анализа и расчета системы конечных элементов действительны все принципы, действующие в дискретной системе.
Этапы дискретизации в методе конечных элементов (рис. 24) [41]:
1) область определения непрерывной величины разбивается на конечное число подобластей (элементов), имеющих общие узловые точки и аппроксимирующих форму области;
2) в рассматриваемой области фиксируется конечное число точек (узлов);
3) значение непрерывной величины в узле считается известным, однако в действительности его еще следует определить при помощи дополнительных ограничений, накладываемых на узел;
4) используя значения непрерывной величины в узлах и аппроксимирующую функцию определяют значение исследуемой величины внутри области.
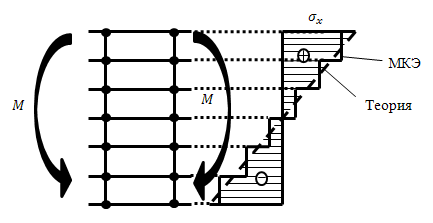
Рис. 24 – Иллюстрация расхождения между результатами, полученными с использованием МКЭ и теоретически верными, появляющегося в силу особенностей дискретизации
По способу исполнения и формулировки основных уравнений или уравнений конечных элемента различают 4 основных вида МКЭ: прямой, вариационный, резидуума, энергетического баланса. Наиболее ясным и простым является прямой метод, так как использует алгебраические уравнения вместо интегральных и дифференциальных [21].