2.2 Выводы

На основании анализа геометрических характеристик и формы исследуемой рамы автомобиля оказалось возможным сделать ряд выводов и замечаний:

1) Рама обладает достаточно большой изгибной жесткостью, так как в ней используются лонжероны закрытого сечения, а поперечины достаточно жестко крепятся к лонжеронам;

2) В связи с большой жесткостью рамы возможно появление высокого уровня напряжений, чем может быть обосновано применение в качестве материала лонжеронов высокопрочной стали 15ГЮТ;

3) В связи с достаточно жестким креплением поперечин к лонжеронам возможно появление значительных напряжений от стесненного кручения, которые на картах напряжений появятся в области крепления лонжеронов;

4) Рама имеет достаточно большие отверстия в лонжеронах в области креплений V и VII поперечин, которые кажутся значительными концентраторами напряжений;

5) Рама обладает характерным для периферийных рам S-образным профилем в двух плоскостях, что позволит ей выдерживать достаточно большие деформации изгиба без возникновения значительных напряжений, которые могли иметь место быть в случае лонжеронов прямой формы;

6) В настоящем исследовании оказалось возможным использование оригинальной сплошнотельной геометрии рамы для расчета напряжений и определения собственных форм колебаний, что подтверждает необходимость разработки новых методик анализа несущих систем;

7) В настоящей работе крепления поперечин, кронштейнов и прочих элементов к раме не были подробно моделированы, что является основным недостатком применяемых моделей, который не мог быть устранен в силу недостатка данных о креплениях в раме.

3 Описание и обоснование распространенных методик расчета рам

3.1 Статические расчеты

Расчет рамы является в значительной мере приближенным и обычно дополняется данными натурных или модельных испытаний. В существующей традиционной практике используются два простейших режима нагружения:

1) изгиб от вертикальной нагрузки с учетом возможного дополнительного динамического нагружения;

2) кручение, возникающее при форсировании автомобилями кюветов, канав, рвов и других препятствий и преодолении неровностей дороги.

Действием инерционных продольных нагрузок, возникающих от веса смонтированных на раме агрегатов при неравномерном движении, зачастую пренебрегают. Не учитываются в расчетах также различные реактивные (тормозные, от картеров силовой передачи, рулевого механизма) моменты, воспринимаемые рамой. [35]

Изгиб от вертикальной нагрузки характерен для прямолинейного равномерного движения автомобиля по ровной дороге, а также для его неподвижного состояния. В этом случае нагружение рамы происходит от агрегатов, установленных на раме, веса которых приводятся к определенным точкам на лонжеронах рамы, либо распределяются по некоторым областям лонжеронов и поперечин. Нагружение симметрично и потому анализируют только половину симметричной модели. Рама претерпевает деформацию изгиба вокруг поперечной оси. Как правило, периферийные рамы неплохо работают на изгиб, обладая достаточной податливостью и в то же время прочностью [11].

На рис. 23 изображена расчетная схема изгибного нагружения, согласно которой поперечины не учитываются, лонжероны представляются балками постоянного сечения, веса агрегатов (радиаторов, двигателя, механизмов управления, кабины) считаются приведенными к точкам лонжерона согласно их центрам масс, а полезная нагрузка в кузове считается распределенной по некоторой длине лонжерона.

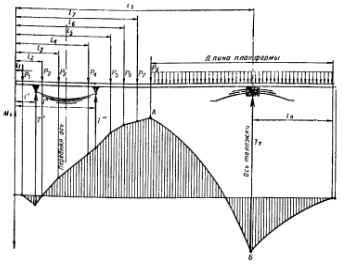
Рис. 23 – Традиционное нагружение рамы при расчете на изгиб: а – расчетная схема; б – эпюра изгибающих моментов

Кососимметричное нагружение автомобиля возникает при движении колесами разных бортов в различных дорожных условиях, как правило – одним бортом по дороге, другим бортом – по обочине, в канаве. Этот вид нагружения имеет множество модификаций, далее будет приведена самая простейшая. Нагружение моделируется в этом случае с использованием тех же нагрузок, что и при расчете на изгиб, но нагрузки на одном из лонжеронов, направленные вниз, меняют свое направление на противоположное. Этот тип нагружения более важен, так как в этом режиме нагружения рама претерпевает совместное действие изгиба и кручения, приводящего к большим напряжениям.

Расчет на кручение обязателен при анализе конструкции рамы. В ходе расчета обычно задаются углом поворота рамы либо смещением в области крепления подвески, однако более правильным решением является расчет ситуации вывешивания колеса, который может возникнуть при движении автомобиля по бездорожью, когда дорожные условия сильно отличаются для каждого из колес. При задании нагружения как правило определяют реакции на колесах и прилагают соответствующие им нагрузки к раме.

Распространена следующая традиционная методика расчета:

1. Определение закручивающего раму момента от дорожных неровностей, по которым движется автомобиль:

, (1)

где - высота неровности;

- колея;

- угловая жесткость подвески;

- угловая (крутильная) жесткость рамы.

Чем меньше жесткость рамы, тем она эластичнее и тем меньше крутильный момент и, следовательно, выше прочность рамы. Кроме того, эластичная рама предоставляет лучшую приспособляемость колесам автомобиля к неровностям дороги. Однако излишняя эластичность рамы нарушает взаимную увязку и центровку агрегатов и частей автомобиля и нежелательна.

Углы закручивания лонжеронных рам обычно составляют 5-10° (15-20° при преодолении препятствий). Крутильная жесткость для штампованных рам принимается Н·м/град, отношение угловых жесткостей рам и подвески изменяется в пределах .

При кручении поперечины искривляются (депланируют), причем депланация по длине поперечины обычно неодинакова, что приводит к стесненному кручению, вызывая помимо касательных напряжений и нормальные, особенно у жестко прикрепленных сваркой, к полкам лонжеронов, а также у усиленных косынками поперечин [14].

2. Определение суммарных нормальных напряжений от чистого изгиба и стесненного кручения:

, (2)

где - изгибающий момент;

- момент сопротивления сечения изгибу;

- бимомент;

- секториальный момент сопротивления.

3. Определение угла закручивания рамы на длине базы при переезде дорожных неровностей (для двухосного автомобиля):

, (3)

где , - углы поворота рамы в поперечном направлении на передней и задней осях;

- момент, закручивающий раму.

4. Определение касательных напряжений кручения. Касательные напряжения кручения можно разложить на касательные напряжения свободного кручения, касательные напряжения изгиба и касательные напряжения стесненного кручения. Как показывает опыт, 90 % касательных напряжений вызываются свободным кручением и для открытого профиля и закрытого профилей соответственно определяются:

, (4)

, (5)

где - модуль сдвига;

- изгибно-крутильная характеристика поперечного сечения;

- удвоенная площадь контура, ограниченного средней линией сечения;

- удвоенный периметр контура, образованного средней линией сечения.

Изгибно-крутильная характеристика сечения стержня определяется:

, (6)

где - длина закручиваемого стержня;

- момент инерции сечения при кручении.

Удвоенная площадь контура :

, (7)

где - ширина профиля;

- высота профиля.

Удвоенный периметр контура :

. (8)

Важным, но редко учитываемым режимом нагружения является возникающий при переезде препятствия колесом, так как в этом случае рама подвергается продольному и вертикальному нагружению. Однако, как показывает опыт, напряжения в раме при таком нагружении меньше, чем при преодолении подъема, характеризующегося наибольшим продольным нагружением, и меньше, чем при обычном изгибе с учетом динамических коэффициентов, поэтому этот режим редко рассматривают.

Преодоление подъема – достаточно распространенная задача при эксплуатации внедорожников, особенно по бездорожью. Если при движении по дорогам общего пользования подъемы и спуски невелики, то на бездорожье углы уклона значительны. В таком режиме нагружения достигается наибольшее продольное нагружение рамы.

Интересен режим бокового нагружения рамы, который может иметь место в случае несимметричных тяговых или тормозных условий на колесах, движения по криволинейной траектории, заноса и удара колесом о препятствие при повороте. Так как последний режим нагружения характеризуется наибольшими напряжениями, вызываемыми боковыми нагрузками, то он моделировался в настоящей работе.