Пример 10

Определить значение теплового потока в зазоре δ=3 мм между двумя трубами длиной l=1 м, если диаметр внутренней трубы равен d=30 мм, между трубами находится трансформаторное масло, а температуры поверхностей труб равны соответственно t₁=80 ºС, t₂=35 ºС.

Решение

Тепловой поток при стесненной конвекции вычисляется по формуле

где λ_эк= ·λ; ε_к=А[Gr·Pr] .

По средней температуре между стенками  ºС определяем параметры трансформаторного масла:

γ=856 кг/м³; υ=5,78·10^-6 м²/с; λ=0,1072 Вт/(м·К); Pr=87,5;

0,0023·9,81·45·30³·10^-9/5,78²·10^-12=8,21·10⁵;

[Gr·Pr]=8,21·10⁵·87,5=718·10⁵.

Тогда коэффициенты А=0,105, r=0,3; ε_к=[8,21·10⁵·87,5]^0,3·0,105=23,9;

λ_эк=23,9·0,1072=2,56 Вт/(м·К); p=2,56(80-35)/0,003=38400 Вт/м².

Пример 11

Определить наибольшую силу тока, пропущенного через электрический нагреватель из нихромовой проволоки диаметров d=1,0 мм, допустимая температура нагрева которой t_доп=1000 ºС. нагреватель находится в спокойном воздухе, температура которого t₀=10 ºС, а конструкция нагревателя такова, что его можно рассчитывать как одиночный цилиндр. Теплоотдачей излучением пренебречь.

Решение

Для свободной конвекции Nu=c[Gr·P²]

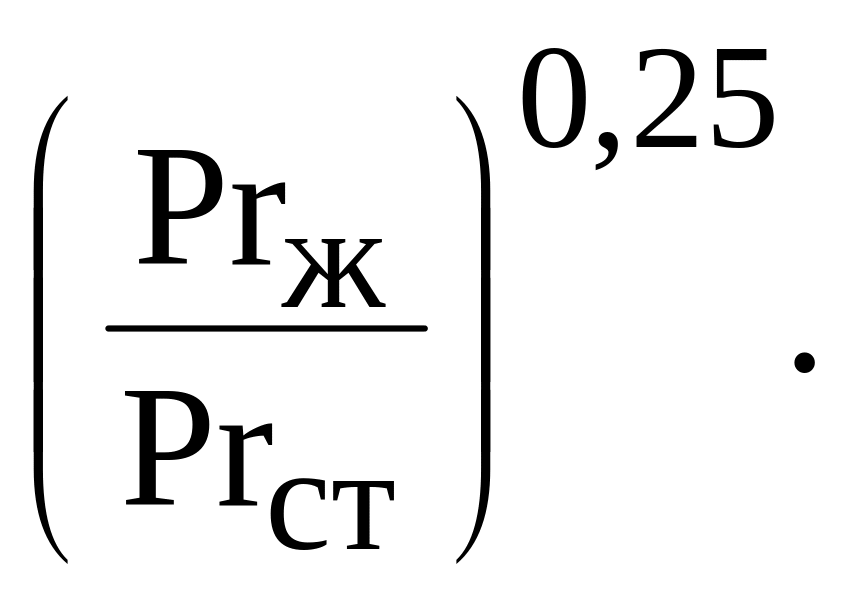
Для воздуха

Определим физические параметры воздуха по средней температуре

ºС:

γ=0,456 кг/м³; с=1093 Дж/(кг·К); λ=5,74·10^-2 Вт/(м·К); υ=79,38·10^-6 м²/с;

Pr=0,687; Gr=pgd³· 0,0013·9,81·10^-9·990/79,38²·10^-12=2;

Тогда [Gr·Pr]=2·0,687=1,374 и коэффициенты с=1,18, n=0,125;

Nu=1,18[2·0,687]^0,125=1,23.

Определим коэффициент теплопередачи из критерия Нуссельта:

Уравнение баланса выделенной и отводимой тепловой энергии имеет вид

где ρ_о=111·10^-8 Ом·м; α=0,00014 К^-1; S=πr²=3,14·0,5²·10^-6=0,785·10^-6 м²; l=1 м; F=πd·1=3,14·10^-3;

Отсюда I=11,6 А.

Пример 12

По внутренней поверхности трубы из нержавеющей стали протекает постоянный ток, в результате чего температура внутренней поверхности t=75 ºС. Внутри трубы протекает вода со скоростью w=0,1 м/с, внутренний диаметр трубы d_вн=7,6 мм, длина трубы l=1 м, а температура воды на входе t_вх=20 ºС, на выходе t_вх=65 ºС. Определить длительно допустимый переменный ток. При t=75 ºС удельное сопротивление нержавеющей стали ρ=0,85·10^-6 Ом·м, а наружный диаметр трубы d_нар=8 мм.

Решение

Определим параметры воды при средней температуре

ºС ≈ 40 ºС:

ρ_стали=0,35·10^-6 Ом·м; α=0,009 К^-1; υ=0,64·10^-6 м²/с;

λ=63,7·10^-2 Вт/(м·К); β=32·10^-4 К^-1; P₂=4,1.

Для стенки при Т_ст=75 ºС Pr_ст=2,39.

Определим режим течения воды:

Значит, режим течения ламинарный и для него

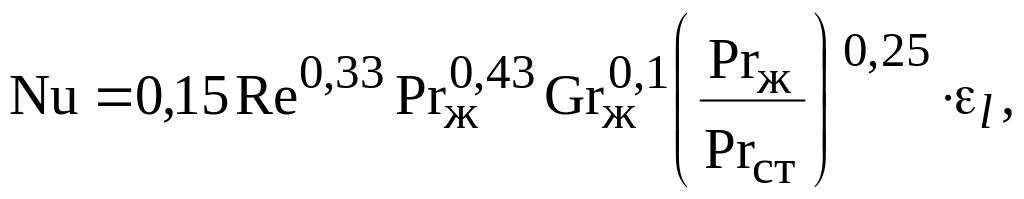
где 0,0032·9,81·3,25·7,6³·10^-9 / 0·642·10^-12=

=1,09·10⁶; l/d=1000/7,6 > 50, тогда ε_l=1,

Nu=0,15·1187,5^0,33·4,1^0,43(1,09·10⁶)^0,1·(4,1/2,39)^0,25=12,94.

Отсюда

Уравнение баланса выделяемой и отводимой тепловой энергии имеет вид

где S=π(4²-3,8²)·10^-6=4,9·10^-6 м²; F=πd_вн·1=3,14·7,6·10^-3=23,86·10^-3 м²;

Отсюда А.

Пример 13

Вычислить допустимый ток катушки индуктивности, выполненной из медной трубы, намотанной на цилиндрическую оправку радиусом R=120 мм. Труба имеет внутренний диаметр d=12 мм, толщину стенки δ=2 мм, и по ней с целью охлаждения пропускают воду со скоростью v=1 м/с. Температура воды на входе t_вх=25 ºС, на выходе t_вых=55 ºС. Катушка имеет 4 витка. Температура внутренней поверхности трубы не должна превышать t_доп=55 ºС. Определить также количество теплоты, отводимое водой от катушки.

Решение

Допустимый ток определим из уравнения баланса тепловой энергии, выделяемой в катушке и уносимой водой:

где ρ_о=1,62·10^-8 Ом·м.

Определим среднюю температуру виды и ее параметры:

γ=992 кг/м³; λ=63,5·10^-2 Вт/(м·К); υ=0,659·10^-6 м²/с; β=3,87·10^-4 К^-1; Pr=4,31; с=184 Дж/(кг·К).

Определим характер течения воды:

Значит, режим течения турбулентный и для него

Nu=0,021Re^0,8·Pr^0,43

Радиус витка R_в=120+14=134 мм = 134·10^-3 м.

Длина витка м.

Длина трубки м.

Тогда для

Коэффициент теплопередачи

Вт/(м²·К); S=π(8²-6²)·10^-6=88·10^-6 м²;

F= πd_внl_тр=3,14·12·10^-3·3,364=126·10^-3 м²;

I²·1,62·10^-8(1+0,0043·65)· ; I=325 А.

Мощность, уносимая водой через сечение трубы, 3,14× ×36·10^-6=113·10^-6 м²; 113·10-6·1·992·4174·30·10-3=14036 Вт.

Пример 14

Определить допустимую плотность тока в медной круглой шине диа­мет­ром d=20 мм, расположенной концентрично в стальной трубе, размеры которой d_вн=1 дюйм и d_нар=33,5 мм. Между поверхностью шины и трубы – глубокий вакуум. Максимальная температура поверхности шины по техническим условиям не должна быть выше t=100 ºС, а температура внутренней поверхности стальной трубы t_тр=35 ºС. Поверхность трубы покрыта белым лаком, поверхность шины – черным матовым.

Решение

Плотность теплового потока излучением, когда одно тело находится внутри другого, определяется формулой

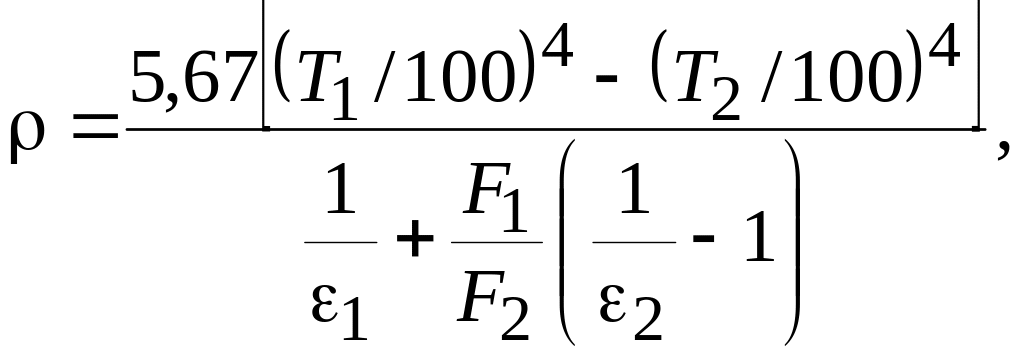
где Т₁ и Т₂ – температуры поверхности медной круглой шины и внутренней поверхности трубы, K; ε₁ и ε₂ – степень черноты полного излучения поверхности шины и внутренней поверхности трубы; F₁ и F₂ – поверхности шины и трубы, м².

Полный поток с поверхности шины длиной 1 м

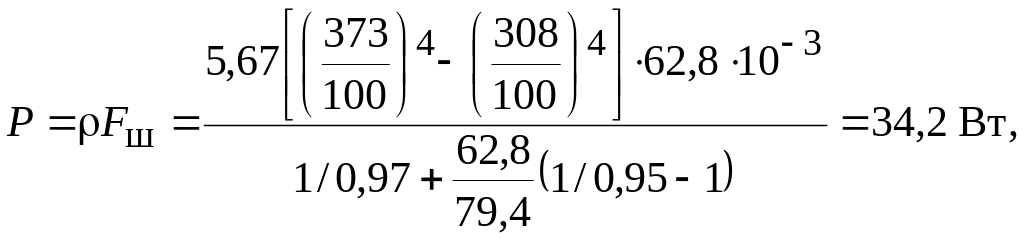
где

=3,14·20·10^-3·1=62,8·10^-3 м²;

Этот поток энергии излучением определяется энергией, выделившейся в шине:

где 3,14·100·10^-6=3,14·10^-4 м²; ρ_о=1,75·10^-8 Ом·м; α=0,0043 К^-1; I=jπ

Тогда =

=

Пример 15

Определить длительно допустимый переменный ток частотой f=50 Гц для медной окисленной шины, расположенной горизонтально на ребре в спокойном воздухе. Размеры поперечного сечения шины 60×6 мм, допустимая температура для этой шины t_доп=80 ºС, а температура окружающей среды t₀=35 ºС.

Решение

В этом случае теплопередача идет за счет излучения и конвекции. Тогда уравнение баланса тепловой энергии имеет вид

где ρ_о=1,75·10^-8 Ом·м; α=0,0043 К^-1; F=0,06·2·1·0,006·2=0,132 м²; S=60·6× ×10^-6=36·10^-5 м².

Определим коэффициент теплопередачи конвекцией. Для средней температуры с=1005 Дж/(кг·К); υ=18,97× ×10^-6 м²/с; Pr_в=0,696; ε=0,6; β=0,003 К^-1.

Для свободной конвекции используем критериальное уравнение

где

Gr =

L=60 мм.

Тогда [Gr·Pr_в]=0,0004·0,696=0,00028.

Отсюда с=0,5, n=0.

Итак,

Из выражения для критерия Нуссельта определим К_Т:

Коэффициент теплопередачи излучением определим по формуле

Отсюда =4,9

Тогда уравнение баланса тепловой энергии примет вид

·1,75·10^-8(1+0,0043·80) (240+5)·0,132·45, откуда I=4721 А.

Пример 16

Определить силу тока электрического нагревателя, предназначенного для обогрева комнаты, в которой температура воздуха Нагреватель изготовлен из нихромовой проволоки диаметром d=1 мм, допустимая температура его Конструкция нагревателя такова, что для его расчета можно воспользоваться критериальным уравнением одиночного цилиндра. Расчет произвести с учетом теплоотдачи конвекцией и излучением. Степень черноты излучения нихрома ε=0,75.

Решение

Уравнение баланса тепловой энергии, выделившейся в нагревателе и отводимой в окружающую среду, имеет вид

где ρ_о=100·10^-8 Ом·м; α=0,00014 К^-1; S= м². F= 3,14·10^-3 м².

Для средней температуры λ=5,74·10^-2 Вт/(м·К); υ=79,38·10^-6 м²/с; Pr=0,687. Для T=1000 ºС Pr=0,719.

Для определения коэффициента теплопередачи конвекцией используем критериальное уравнение для свободной конвекции:

где ≈1 для воздуха; ;

Тогда с=1,18; n=0,125;

Отсюда коэффициент теплопередачи конвекцией

.

Тепловой поток за счет конвекции

Тепловой поток излучением

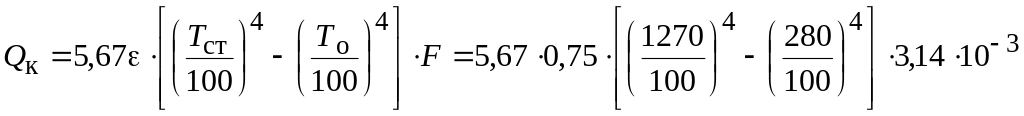= =346 Вт,

где ε=0,75;

Пример 17

Определить тепловое сопротивление и тепловой поток через чугунную стенку толщиной δ=10 мм, которая является стенкой масляного бака и имеет площадь S=2 м², если известно, что температура масла в баке равна 85 ºС, а температура наружной поверхности бака – 45 ºС. Теплопроводность чугуна λ=47 Вт/(м·К) при 0 ºС, температурный коэффициент теплопроводности β=-4·10^-4 К^-1.

Решение

Тепловое сопротивление стенки бака где δ – толщина стенки, м; S – площадь стенки бака, м²; λ – коэффициент теплопроводности, Вт/(м·К).

Для средней температуры λ_о=47 Вт/(м·К) и λ= λ_о× ×(1- βТ_ср)=47(1-4·10^-4·65)=45,78 Вт/(м·К).

Тогда К/Вт и тепловой поток Вт.

Пример 18

Определить температуру прямоугольной алюминиевой шины с размерами поперечного сечения 100×10 мм, покрытой слоем бумажной изоляции толщиной δ=3 мм, если известно, что по шине протекает постоянный ток I=2000 А. Температура наружной поверхности изоляции t_из=40 ºС.

Решение

По закону Ома для передачи энергии теплопроводностью

Т_ш-Т_пов=R_т·Р,

где Т_ш, Т_пов – температура шины и наружной поверхности изоляции, ºС; Р – тепловой поток с поверхности шины, Вт; R_т – тепловое сопротивление слоя изоляции, К/Вт.

Тепловой поток с поверхности шины определяется энергией, выделившейся в шине при прохождении тока, и равен

где ρ_о=2,62·10^-8 Ом·м; α=0,0042 К^-1; λ_из=0,14 Вт/(м·К); S=0,1·0,01=10^-3 м²;

К/Вт; F=0,1·2+0,01·2=0,22 м².

Тогда 0,097·(104,8+0,44Т_ш) = Т_ш–40, Т_ш=52,3 ºС.

Пример 19

Определить температуру наружной поверхности изоляции круглого медного проводника диаметром d=40 мм, по которому протекает ток I=2250 А, в результате чего поверхность оказывается нагретой до температуры t=60 ºС. Проводник покрыт двумя изоляционными слоями: слоем бумаги с теплопроводностью λ₁=0,1 Вт/(м·К) и слоем лакоткани с теплопроводностью λ₂=0,1 Вт/(м·К). Толщина бумажной изоляции δ₁=4 мм, толщина изоляции из лакоткани δ₂=6 мм.

Решение

По закону Ома для теплопередачи теплопроводностью

где – тепловое сопротивление слоев бумаги и лакоткани, К/Вт; – температуры проводника и наружной поверхности изоляции соответственно, ºС,

;

λ₁=0,14 Вт/(м·К) (бумага); λ₂=0,18 Вт/(м·К) (лакоткань); l=1 м;

К/Вт;

Вт;

ρ_о=1,75·10^-8 Ом·м; α=0,0043 К^-1; S= =3,14·400·10^-6=1256·10^-6 м².

Подставляя полученные значения в первую формулу, получим

(0,209+0,197)·89=60-Т_нар, Т_нар=24 ºС.

Пример 20

Вычислить допустимую силу тока алюминиевого проводника круглого поперечного сечения диаметром d=40 мм, покрытого двумя изоляционными слоями: слоем бумаги, толщина которого δ₁=4 мм, и слоем лакоткани, толщина которого δ₂=6 мм. Допустимая температура наружной поверхности изоляции t₂=70 ºС, внутренней поверхности t₁=80 ºС. Теплопроводность для бумаги λ₁=0,1 Вт/(м·К), для лакоткани λ₂=0,1 Вт/(м·К).

Решение

По закону Ома для теплопередачи теплопроводностью

,

где – температуры внутренней и наружной поверхностей изоляции, ºС; – тепловые сопротивления слоев бумаги и лакоткани соответ­ственно,

К/Вт;

К/Вт;

ρ_о=2,62·10^-8 Ом·м; α=0,0042 К^-1; S= =3,14·400·10^-6=1256·10^-6 м².

Подставив полученные значения в первоначальное выражение, получаем

(0,29+0,177)·0,0000278I²=80-70; I=277 А.

Пример 21

Определить температуру поверхности стальной трубы, по которой протекает переменный ток I=450 А частоты f=50 Гц. Труба окрашена мас­ляной краской (внутренний диаметр d_вн=3 дюйма, наружный d_нар=88,5 мм), расположена горизонтально в спокойном воздухе, температура которого t₀=35 ºС.

Решение

Уравнение баланса тепловой энергии, выделяющейся в проводнике и отводимой с его поверхности, имеет вид

где К_п – коэффициент поверхностного эффекта, определяемый по формуле

Тогда м, =1,5.

Коэффициент теплопередачи

,

где К₁=1,08 Вт/(м²·К), К₂=0,75 К^-1 определяются в зависимости от диаметра.

м; ;

ρ_о=2,62·10^-8 Ом·м; α=0,009 К^-1.

Подставляем все величины в первоначальное уравнение:

1,5·450²·12·10^-8·(1+0,009T₁)· 10·1,08·[1+0,75·10^-2(T₁-35)]-0,28·(T₁-35).

После преобразований получаем

0,023 ;

Отсюда .

Ответ: Т₁=44,81 ºС.

Пример 22

Определить температуру оси круглой шины диаметром d=15 мм. По шине протекает ток I=6000 А. Температура потока воды, который ее обтекает, t₀=25 ºС. Коэффициент теплоотдачи с поверхности шины k_т=1000 Вт/(м²·К). Удельное сопротивление материала шины ρ=2,2·10^-8 Ом·м, теплопроводность λ=400 Вт/(м·К).

Решение

Уравнение баланса тепловой энергии, выделяющейся в шине и отводимой в окружающую среду, имеет вид

Т_оси-Т_с=РR_Т, (1)

где Т_оси – температура на оси шины; Т_с – температура поверхности шины;

Так как в первоначальном уравнении два неизвестных, то дополняем его уравнением тепловых потерь:

Р=К_ТF(Т_с-Т_ж). (2)

Находим тепловое сопротивление шины:

К/Вт.

Выразив Т_с из (1) и подставив его в (2), получим

Р=К_ТF(Т_осн-РR_Т-Т_ж).

Отсюда

Т_осн= Т_ж,

где Вт; F=πd·1=3,14·15·10^-3 м².

Тогда Т_осн= ºС ≈121,4 ºС.

Пример 23

Определить допустимый ток для медной шины, поперечное сечение которой 120×10 мм. Шина установлена на ребро в спокойном воздухе горизонтально. Частота переменного тока f=50 Гц, допустимая температура шины t_доп=85 ºС, температура окружающей среды t₀=35 ºС. Полученный результат сравнить с результатом, который получился бы для круглой шины при условии, что площадь ее поперечного сечения равна площади поперечного сечения прямоугольной шины.

Решение

Уравнение баланса выделяющейся в шине тепловой энергии и энергии, отводимой в окружающую среду, имеет вид

где 164,7, откуда ≈1; Ом; S=0,12+0,1=0,0012 м²; F=0,12× ×2+0,01·2=0,26 м²; α=0,0043 K^-1; ρ_o=1,61·10_-8 Ом·м; К_т=9,2[1+0,9·10^-2(Т_доп-

-Т_о)]= 9,2[1+0,9·10^-2(85-35)]=13,34 Вт/(м²·К).

Тогда I²·1,62·10-8(1+0,0043·85)·

Отсюда I=2940 А.

Пример 24

Определить время, через которое медная шина с размерами поперечного сечения 100×6 мм нагреется переменным током I=500 А до температуры t=100 ºС, если она находится в спокойном воздухе с температурой t₀=35 ºС, коэффициент теплоотдачи с наружной поверхности шины k_т=15 Вт/(м²·К), а начальная температура шины t_н=50 ºС.

Решение

Уравнение процесса нагрева при теплоотводе в окружающую среду имеет вид

.

Здесь , где F=0,1·2+0,006·2=0,212 м²; × Вт,

-35= , откуда Т_уст=315 ºС.

Постоянную времени нагрева определим по формуле

с, так как »

с=390 Дж/(кг·К); γ=8700 кг/м³; m=8,799·6·10^-4=5,2 кг.

Подставляем полученные значения в исходное выражение:

100=315·(1- )+50 .

Отсюда t≈134 с.