Пример 5

Определить значение коэффициентов перегрузки по мощности и току стальной шины прямоугольного сечения 100×4 мм, нагреваемой прерывистым током I=600 А через установленные промежутки времени. Допустимая температура нагрева шины t_доп=95 ºС. Шина находится в спокойном воздухе, температура которого t_доп=35 ºС, коэффициент тепло­отдачи с поверхности шины k_т=12 Вт/(м²·К), температура шины в результате протекания прерывистого тока достигает t=95 ºС.

Решение

Для стальной шины γ=7800 кг/м³; ρо=11·10^-8 Ом·м; с=470 Дж/(кг·К); α=0,009 К^-1.

Коэффициент перегрузки по току и мощности определяется следующими выражениями:

Определим длительно допустимый ток:

где S=0,1·1·2+0,004·1·2=0,208 м² – площадь теплоотдающей поверхности;

Отсюда I_дл=541,8 А.

Коэффициент перегрузки по току

Коэффициент перегрузки по мощности

Пример 6

Определить температуру алюминиевой шины прямоугольного сечения размером 40×5 мм после протекания по ней тока I=20000 А в течение времени t=1 с. Начальная температура шины t_н=0 ºС.

Решение

Для Al γ=2700 кг/м³; ρ=2,62·10^-8 Ом·м; с=950 Дж/(кг·К); α=0,0042 К^-1.

Масса шины длиной 1 м т=0,04·0,005·1·2700=0,54 кг.

Тогда постоянная времени нагрева

где F=0,04·1·2+0,005·1·2=0,09 м².

Отношение < 0,1 c.

Значит, процесс нагрева можно считать адиабатическим и температуру проводника можно определить по кривой адиабатического нагрева для алюминия (см. рис. П8 [ ]).

Для нашего случая и , где , А/м².

Пример 7

Определить температуру нагрева медной прямоугольной шины с размерами поперечного сечения 80×10 мм в результате протекания по ней в течение 8 с тока КЗ с параметрами I_~p=90000 А, I_∞=90000 А, если известно, что в начальный момент КЗ по шине протекал номинальный ток и температура шины при этом составляла t_нач=90 ºС. Шина находится в спокойном воздухе.

Решение

Определим фиктивное время КЗ по рис. П.10 [ ]. При t_КЗ>5 с считаем, что ток КЗ равен установившемуся току.

Тогда полное фиктивное время КЗ

где t_ф' – фиктивное время КЗ при t_КЗ= 5 с.

Для нашей задачи при имеем 5,5 с. Тогда полное фиктивное время КЗ

При начальной температуре Т=90 ºС квадратичный импульс тока по П.8 [ ] А²с/м⁴.

При t_ф=8,5 с квадратичный импульс тока

А²с/м⁴,

где S=0,08·0,01=0,0008 м².

Суммарный импульс тока

А²с/м⁴.

Ему соответствует, по кривым адиабатного нагрева П.8 [ ], Т≈240 ºС.

Пример 8

Определить ток 10-секундной термической стойкости для стальной шины прямоугольного сечения размером 100×4 мм, находящейся в спокойном воздухе, для случая, когда начальная температура шины t_нач=80 ºС. Для стальной шины допустимая температура в кратковременном режиме нагрева t_доп=300 ºС.

Решение

При t_{доп.стали}=300 ºС квадратичный импульс тока А²с/м⁴.

При t_нач=80 ºС А²с/м⁴.

Тогда ток термической стойкости равен где S=0,1·0,004=0,0004 м², , I=6930 А.

Пример 9

Определить коэффициент теплоотдачи с поверхности цилиндрического проводника, расположенного горизонтально в спокойном трансформаторном масле, температура которого t_с=75 ºС, диаметр d=45,0 мм.

Решение

Коэффициент теплопередачи К_Т определить из критерия Нуссельта где 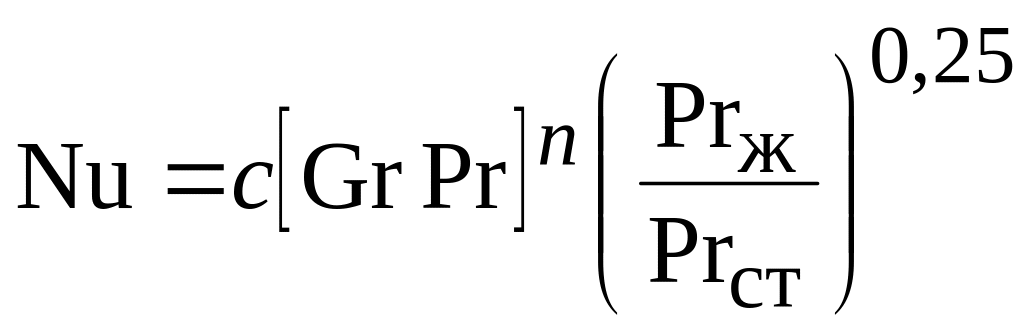, где Gr, Pr – критерии Грасгофа и Прандтля; L – характерный геометрический размер (для цилиндра – диаметр).

Физические параметры трансформаторного масла определяем по средней температуре:

ºС;

γ=862 кг/м³; с=184 Дж/(кг·К); λ=0,1082 Вт/(м·К); υ=7,58·10^-6 м²/с;

Pr_ж=111, Pr_ст=60; β= К^-1.

Находим [Gr·Pr]=2,65·10⁶·111=2,94·10⁸, где

Тогда коэффициенты с=0,135 и n=0,33.

Определим критерий Нуссельта:

Nu=0,133

Отсюда Вт/(м²·К).